
이 글은 Networkx를 활용한 네트워크 분석 기초 입문 정리 - 박건영 저 (E-book) 를 읽고 개념 정리를 한 글입니다.
회사에서 진행하는 단기 프로젝트는 끝났지만 이왕 책을 산김에 정리해야겠다는 생각이 들어 마저 작성한다. 두번째 글은 네트워크 분석에 대해서 더 깊이 들어간다.
4장. 네트워크 시각화
4.1 네트워크 시각화의 주요 개념
(1) 네트워크 시각화 (Network Visualization)
네트워크 시각화의 표현에는 그래프 형태 표현 / 트리 형태 표현 / 다차원 척도 형태 표현으로 구반할 수 있다.
(2) 배치 (Layout)
각 노드들 간 연결관계를 토대로 노드들의 좌표를 계산하여 해당 노드들을 네트워크 지도에 배치하고 그들의 연결관계를 표시하는 작업 (Drawing)을 의미
배치 알고리즘으로 수행되며 주요 고려사항은 차원 (=노드와 링크의 배치공간), 규모 (=소규모 또는 대규모 네트워크 여부)
4.2 그래프 형태의 네트워크 시각화
그래프 형태: 평면상 그래프를 그렸을 때 노드들 간 링크가 교차하지 않는 평면 그래프 를 그려야 한다.
- 링크들이 연결되는 길이 최소화
- 링크 길이 균등화, 계량 그래프에서는 가중치에 비례하게 링크 길이를 표시
- 가능한 굴곡선이 없도록 한다.
주로 배치 알고리즘은 2D를 사용한다.
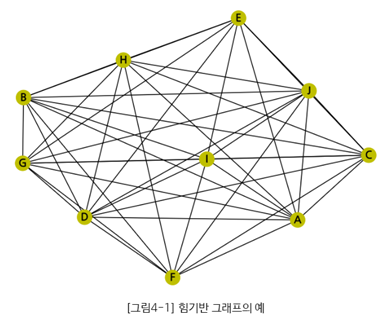
(1) 힘기반 그래프 배치 (Force-based Graph Layout) 알고리즘
그래프 노드들을 2차원 또는 3차원 공간에 배치시켜 링크들의 거리를 거의 균등하게 하고 링크들이 서로 교차하는 것을 최소화하는 방식으로 그래프를 그리는 알고리즘
노드들의 집합과 링크들의 집합을 대상으로 적절한 인력과 척력을 부여하는 방식 사용
스프링 계의 물리시스템과 유사한 방시긍로 전체 노드들이 평형 상태를 유지하게해 스프링 매듭 (Spring Embedding) 알고리즘 이라고도 한다.
- 유연하고 직감적이고 단순하다
- 그리는 시간이 많이 소요 된다.
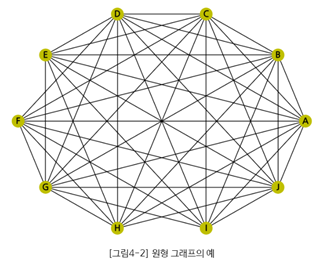
(2) 원형 (Circular) 알고리즘
- 단일 원형 알고리즘: 하나의 원주 공간에 일정 간격으로 노드를 배치하여 연결관계 그리는 방식
- 복수 원형 알고리즘: 복수의 원형 공간에 노드들을 배치해 연결관계 그리는 방식
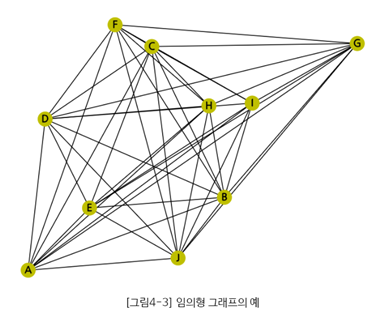
(3) 임의형 (Random) 알고리즘
노드들의 좌표값을 계산하거나 임의로 부여하여 그래프를 그리는 방식
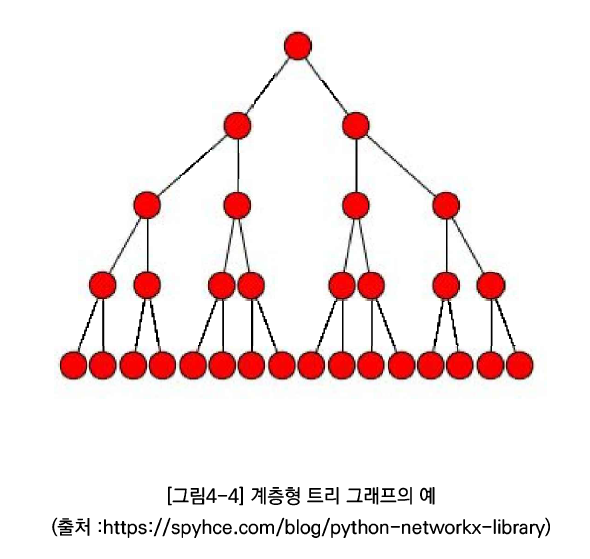
4.3 트리 형태의 네트워크 시각화
(1) 계층형 트리
링크를 계층화하여 표현하는 방식, 노드 쌍이 “부모-자식 관계 형태” 일 때 사용
동일 계층 노드는 수평 배치, 링크는 수직 배치 => 수평-수직 배치 (Horizontal & Vertical Layout = HV – Layout) 방식
계층 많아지면 화면 배치 비효율적이 되고, 루트 노드 주변 낭비가 심해진다.
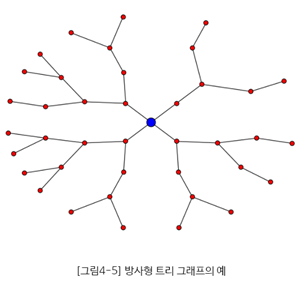
(2) 방사형 트리
계층형 트리의 화면 낭비 문제 해결 방안으로, 하위 계층 노드들을 방사형 배치하는 방식
핵심 노드는 가장 중앙에 있고, 다른 노드들은 외부의 원형 상에 배치
핵심노드와 다른 노드들 간 거리는 최단경로거리(=트리 상 깊이)와 가능한 비례하게 표현한다.
4.4 다차원 척도 형태의 네트워크 시각화
다차원 척도 방식: 다차원 척도법 (Multi-dimensional Scale, MDS) 을 활용하여 네트워크 시각화하는 방법으로,노드들의 거리를 토대로 유사성과 상이성 구한 뒤 다차원 공간에 기하학적으로 표현하는 방식이다.
입력자료가 등간척도 또는 비율척도인 경우
-> 고전적 MDS (Classic MDS, Metric MDS)
서열척도인
-> 비계량 MDS (Non-metric MDS)
노느들의 군집성을 보여주기는 하지만, 노드들 간 연결 관계를 나타내진 못함.
4.5 대규모 네트워크의 시각화
이부분은 조금 들어본 듯한 부분이다. 그만큼 중요하단 얘기겠지.
(1) 최소 신장트리 (Minimal Spanning Tree: MST)
신장 트리: 해당 그래프의 부분 그래프면서 동시에 모든 노드들을 연결하는 트리
최소 신장트리: 각 링크에 비용이 주어질 경우, 최소 비용의 신장트리
(2) 패스파인더 (Pathfinder Network: Pfnet)
데이터의 유사성 또는 상이성 분석을 기반으로 한 시각화, 네트워크 척도를 표현한다.
노드 쌍에 대한 “근접성 (Proximities)” 에서 도출되며, 근접성 패턴에 따라 네트워크의 링크 모양이 결정된다.
보통 특정 영역의 키워드나 개념을 기술하는 지식 네트워크의 시각화에 많이 사용,
노드는 키워드 (또는 개념), 링크는 키워드 사이에 존재하는 근접성 (유사성) 패턴 키워드를 나타내는 노드와 노드 간의 유사성이 높으면 링크가 생성된다.
5장 네트워크 분석 기법의 개요
네트워크 분석 기법은 분석 수준에 따라 크게 6가지 유형으로 나뉜다.
- 네트워크 수준 분석
- 노드 수준 분석
- 네트워크에 내재된 특성 분석
========================여기까지가 기본 속성 분석 - 중심성 분석
- 하위집단 분석
- 에고 네트워크 수준 분석
(1) 네트워크 수준 분석
네트워크 전체의 특성을 분석하는 방법, 거시 (Macro) 수준의 분석
주로 네트워크 크기, 네트워크 밀도 등의 분석지표를 사용
(2) 노드 수준 분석
각 노드의 특성, 노드들 간의 링크 관계에 대한 특성을 분석하는 방법, 미시 (Micro) 수준의 분석
주로 연결정도, 연결강도, 연결거리, 경로 등의 분석지표를 사용
(3) 네트워크에 내재된 특성 분석
하이브리드 (Hybrid) 수준의 분석
주로 특정 노드들이 밀접하게 구성되는 상호성, 이행성, 군집화 계수 등의 분석지표를 사용
(4) 중심성 분석
네트워크 내 각 노드들의 영향력 크기를 분석하는 방법
주로 연결정도 중심성, 근접 중심성, 매개 중심성, 파워 중심성, 아이겐벡터 중심성 등의 분석지표 사용
(5) 하위집단 분석
전체 네트워크에서 하위 집단을 구분하고 그것을 대상으로 분석하는 방법
주로 컴포넌트 분석, 파당 분석 등의 분석지표를 사용
(6) 에고 네트워크 수준 분석
특정 에고를 중심으로 형성되는 네트워크 특성 분석하는 방법
에고 네트워크 특성 분석 (크기, 밀도, 성분 등), 중개성 분석, 구조적 공백 분석 (중복성 제약성, 효과크기) 등의 분석지표 사용
6장 네트워크 수준 분석
6.1 네트워크 크기 (Network Size)
네트워크를 구성하는 노드의 수 = 크기 = 규모
링크의 수를 포함하여 나타내기도 함.
노드 수가 n이면
방향 네트워크에서는 n (n-1) 개의 연결 관계를 가진 노드 쌍
무방향 네트워크에서는 n (n-1) / 2 연결 관계를 가진 노드 쌍
6.2 밀도 (Density)
밀도: 네트워크 노드들 사이 연결되는 정도, 전체 노드들의 연결된 개수로 표현
고립노드: 네트워크 내 다른 노드들과 연결 관계가 전혀 없는 노드
공식: 밀도 = 실제 연결된 링크 수 / 연결 가능한 전체 링크 수
밀도는 0~1 사이이고, 0이면 연결선 없는, 1이면 모든 노드 연결된 네트워크이다.
(1) 무방향/이진 네트워크의 밀도
실제 연결된 링크 수 = k, 노드 수가 n이면
네트워크 밀도 = k / {(n*(n-1)/2}
(2) 방향/이진 네트워크의 밀도
실제 연결된 링크 수 = k, 노드 수가 n이면
네트워크 밀도 = k / (n*(n-1))
(3) 계량 네트워크의 밀도
평균 연결강도(=연결된 모든 에지의 관계강도 수치를 합산한 값) / 연결가능 노드 수
6.3 포괄성 (Inclusiveness)
포괄성: 전체 노드 수에서 고립된 노드의 수를 제외한 수 또는 비율을 의미, 네트워크에서 연결되지 못한 노드들의 크기에 대한 지표이다.
(1) 절대적 포괄성: (전체 노드의 수) - (고립 노드의 수)
(2) 상대적 포괄성: (링크가 있는 노드의 수) / (전체 노드의 수)
7장 노드 수준 분석
7.1 연결정도 (Degree)
연결정도: 임의의 해당 노드에 직접 연결된 노드들의 개수 (또는 연결선의 개수)
-> 특정 노드의 영향력을 파악하는 지표
연결정도가 높으면 해당 노드는 전체 네트워크에서 영향력이 높다고 판단
(1) 연결정도 계산법
네트워크 내 형성된 각 노드들 간의 상대적 순위를 의마하게 됨.
보통은 상대적 연결 계산법 사용
1) 절대적 연결 계산: 노드에 연결된 링크 수
2) 상대적 연결 (정규화된 연결): 노드에 연결된 링크 수에 대해 정규화하여 계산한 값
(2) 내향 연결정도(In-degree)와 외향 연결정도(Out-degree)
방향 네트워크의 경우 연결정도가 내향 연결정도와 외향 연결정도로 구분
1) 고립자 (Isolated Node): 내향 연결정도 = 0, 외향 연결정도 = 0
2) 전달자 (Transmitter): 내향 연결정도 = 0, 외향 연결정도 > 0
3) 수신자 (Receiver): 내향 연결정도 > 0, 외향 연결정도 = 0
4) 매개자 (Carrier): 내향 연결정도 > 0, 외향 연결정도 > 0
(3) 연결정도 분포 (Degree Distribution)
네트워크의 구조적 특성을 파악할 수 있다.
분포 P(k)는 임의로 선택된 노드의 연결정도 값이 k가 되는 비율 또는 확률로 계산
P(k)가 정규분포 또는 포와송 분포인 경우에는 무작위 네트워크라 칭함.
무작위 네트워크는 연결정도 빈도 비율이 평균값을 중심으로 좌우로 나누어지는 분포, 대부분의 노드들은 거의 같은 개수의 링크를 갖고있다고 해석 가능하다.
연결정도 분포가 멱함수 법칙을 나타내는 분포인 경우 해당 네트워크를 무척도 네트워크라 한다. 멱함수 분포의 네트워크는 네트워크 전체를 규정할 수 있는 노드의 발견 어렵고, 단지 작은 연결정도의 값을 가진 수많은 노드에서 큰 연결정도의 값을 가지는 극소수의 허브 노드(Hub Node)에 이르는 연속적인 값의 분포만 존재.
허브 노드는 예외적일만큼 매우 큰 연결정도 가짐.
통상 계산시에는 연결정도 평균 (Average Degree) 사용
1) 무방향 네트워크에서 연결정도 평균
A = 시그마 k = 1부터 n까지 [k*P(k)] = (2 * E) / n
n: 노드 수, E: 링크수
2) 방향 네트워크에서 내향 연결정도 평균
Ain = 시그마 k = 1부터 n까지 [Kin * P(Kin)] = Ein / n
n: 노드 수, Kin: 내향 연결정도, Ein: 내향 링크 수'
3) 방향 네트워크에서 외향 연결정도 평균
Aout = 시그마 k = 1부터 n까지 [Kout * P(Kout)] = Eout / n
n: 노드 수, Kout: 외향 연결정도, Eout: 외향 링크 수
7.2 연결강도 (Strength)
연결강도: 계량 네트워크에서 두 노드가 링크로 연결되는 강도 (크기)를 의미, 링크간 상대적 비교가 되는 가중치 수치를 나타냄.
이진네트워크에서는 단순 연결 여부만 나타내서 연결강도는 보통 '1'
연결강도는 노드 간 연결의 중요도를 표시하는 지표, 두 노드 간의 형성된 친밀도, 신뢰, 접촉 빈도 등을 의미한다.
(1) 강한 연결/약한 연결
연결강도가 크면 강한 연결, 작으면 약한 연결
적절한 기준값이 제시되어야하며, 계량 네트워크 분석시 또는 이진 네트워크로 변환시에 적부 판단을 위해 필요하다.
보통 등간 데이터 또는 완전(비율) 데이터로 측정되므로 연결강도 간 차이 식별할 수 있다.
(2) 연결강도 표시법
보통 선 굵기 여부로 표현하거나, 해당 링크에 가중치를 직접 표시한다.
7.3 연결거리 (Distance)
연결거리: 특정 노드 간에 연결된 거리를 의미, 또는 단계로도 표현한다.
길이 개념을 강조하는 경우 "경로거리" (Path Length)라고 한다.
다양한 경로가 존재하는 경우 노드 간 연결거리는 최단 연결거리를 나타낸다.
정보, 소문 등의 신속한 전파여부를 판단하는 지표, 중심성 분석 / 하위집단 분석 등에서 많이 활용되며, 네트워크 내 노드들의 결속성을 분석하는 척도로도 활용 가능하다.
7.4 직경 (Diameter)
직경: 네트워크 내 연결거리 중 가장 긴 연결거리
네트워크 내 가장 멀리 떨어진 두 노드 간의 거리이므로 네트워크의 지름이라고도 한다.
7.5 평균 연결거리 (Average Distance)
평균 연결거리: 네트워크 내 모든 노드 쌍의 연결거리에 대한 평균
평균연결거리는 평균거리, 평균경로길이, 특성경로길이, 특성연결거리로 표현하기도 한다.
군집화 계수와 함께 좁은 세상 네트워크의 속성을 파악하는데 유용하게 사용
(1) 평균 연결거리 계산법
n개의 노드를 가진 임의의 네트워크 G에서 노드 Ni와 Nj 간의 최단 연결거리를 D(i, j), 노드 Ni에서 네트워크 내 모든 노드들 (Nj: j는 노드 i를 제외한 모든 노드들)에 이른 최단연결거리의 평균을 D(i)라고 할 때
평균 연결거리 D(g) [=모든 노드들(Nn: n은 n개 노드)들의 각 D(n)의 평균]: D(G) = 시그마 k=1부터 n까지 D(i)
n: 노드 수, D(i): 노드 i의 최단연결거리 평균
7.6 도달가능성 (Reachability)
도달가능성: 임의의 두 노드 간의 도달 가능 여부를 나타내는 개념
0 또는 1로 표시
대칭, 무방향 네트워크: 각 노드쌍은 서로 도달이 가능(1) 또는 불가능(0) 중 하나만 존재
비대칭, 방향 네트워크: A -> B로는 도달 가능, B -> A로는 도달 불가능도 됨.
네트워크는 하나 이상의 컴포넌트들로 구성되어 있으며, 결국 이는 전체 네트워크에서 도달 가능한 노드들로 구성된 몇개의 하위 컴포넌트를 구별해낼 수 있다.
7.7 보행 (Walk)
보행: 두 노드 쌍에 존재하는 길을 의미, 어떤 노드에서 다른 노드로 도달하기 위한 인접한 노드들의 순서열을 말한다.
보행은 경로와 달리 한번 사용한 링크를 반복해서 사용가능하다.
두 노드에 대해 도달가능성이 1일 경우 보행은 존재, 0일 경우 보행은 없다.
(1) 닫힌 보행 (Closed Walk): 시작 노드와 끝 노드가 동일한 보행
(2) 사이클 (Cycle): 3개 이상의 노드들 사이에 이루어진 닫힌 보행
(3) 보행의 길이: 보행에 포함된 링크 수
7.8 경로 (Path)
경로: 보행의 일종, 두 노드 쌍 사이에 링크의 반복을 허용하지 않으면서 두 노드를 연결하는 거리를 의미
(1) 닫힌 경로: 시작 노드와 끝 노드가 동일한 경로
(2) 최단거리경로 (Geodesics): 두 노드간 경로 중 가장 거리가 짧은 경로
연결거리는 두 노드를 최단으로 연결하는 단계의 크기 (수), 최단거리경로는 연결거리의 경로 자체를 의미
우선 7장까지만 정리를 마치고, 추후에 네트워크 분석을 할 일이 있으면 다시 읽어볼 예정이다. 지금 당장 정리해야될게 너무 산더미이다.ㅠㅠ
다음 목차는 이런 순으로 되어 있으며
모든 자료의 출처: Networkx를 활용한 네트워크 분석 기초 입문 정리 - 박건영 저 이다.8장 네트워크에 내재된 특성 분석 - 상호성, 이행성, 군집화 계수, E-I 지수
9장 중심성 분석 - 중심성 개념, 무방향 네트워크에서의 중심성 (연결정도 중심성, 근접 중심성, 매개 중심성), 위세 중심성 (아이겐벡터 중심성), 방향 네트워크에서의 중심성, 계량 네트워크의 중심성, 집중도
10장 - 하위집단 분석 - 컴포넌트 분석, 파당 분석 (n-파당 분석, k-플렉스 분석, k-코어 분석, n-클랜 분석, n-클럽 분석)
11장 에고 네트워크 수준 분석 - 에고 네트워크의 주요 분석 지표 (기본적 분석 지표, 부가적 분석 지표), 중개성 분석, 구조적 공백 분석 (구조적 공백의 계산)
