BOJ 1005 | ACM Craft

뉴비절단기로 악명높은 ACM Craft이다. solved.ac가 활성화된 지금은 문제의 난이도를 티어로 볼 수 있고. Class로 분류되어 있는 좋은 문제들이 많아 뉴비가 멋모르고 이 문제에 접근할 일은 많지 않다.

그러나 solved.ac이 없었던 시절에는 백준을 1000번부터 푸는 뉴비들이 많았기 때문에 A+B, A-B를 풀다가 1005번에서 이 문제를 보게 되는 것이다. (물론 1002~1004번도 그렇게 만만한 문제들은 아니다.)

나도 옛날에 이 문제를 보고 풀다가 던졌던 기억이 있기에 Class 5 순회 중에 만난 이 문제는 마치 운명과도 같았다 할 수 있다. 이제는 할 수 있다 라고 말해주는 듯한 solved.ac의
시프트 마음대로'를 믿고 1005번에 도전했다.

가장 처음 생각한 아이디어는 위상 정렬이다. 건물 건설 순서는 그래프로 나타낼 수 있고, 위상 정렬을 통해 수행 순서를 정렬할 수 있다.

다만 걱정되는 것이 있었는데, 바로 다음과 같은 경우이다.

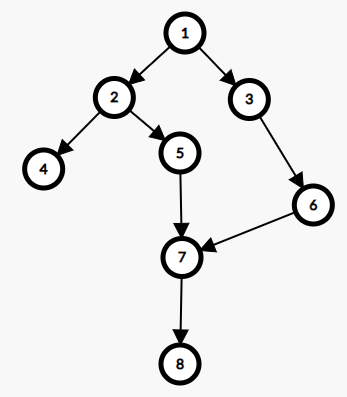
여기서는 dfs를 이용한 위상 정렬을 시도하면 [1 3 6 2 5 7 8 4] 가 되는데, 4의 건설 시간을 계산하기 위해 1 -> 2 -> 4 만 계산하는 것이 아니라 배열에 있는 모든 경로를 다 계산하는 일이 벌어지게 된다.

그래서 이 부분에 대한 예외 처리가 필요한 게 아닌가 생각했으나 어차피 $N$이 최대 1000까지라서 전부 계산해도 시간 초과가 날 것 같지는 않았다.

위상 정렬된 배열을 $order$ 배열이라고 하면, $order$의 모든 원소에 대해 순서대로 시간 계산을 수행한다.

어떤 원소 $i$에 대해, $i$의 건설은 $i$의 모든 부모 노드가 건설된 후 진행된다.

따라서 건설 시간 $t[i]$는 $max(t[parent(i)_1], t[parents(i)_2], ...) + t[i]$로 갱신할 수 있다.

모든 노드 $i$는 단 한번만 갱신되므로 초기에 입력받은 배열 $t[]$에서 모든 연산을 수행할 수 있다.

$order$에 정렬된 순서에 따라 갱신을 수행하면 $t[i]$가 갱신될 때 $t[i]$가 갱신되기 위해 필요한 $parent(i)[]$는 모두 갱신된 상태라 별다른 예외처리 없이 문제를 해결할 수 있다.

코드

#include <bits/stdc++.h>
using namespace std;

#ifdef LOCAL
constexpr bool local = true;
#else
constexpr bool local = false;
#endif

#define FASTIO ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);

#define debug if constexpr (local) std::cout
#define endl '\n'

int T, N, K;

int t[1001];
vector<int> parents[1001];
vector<int> graph[1001];
int visited[1001];

vector<int> order;

void dfs(int x){
	visited[x] = 1;
	for (auto &i: graph[x]){
		if (!visited[i]) dfs(i);
	}
	order.push_back(x);
}

void Tpsort(){
	for (int i = 1; i <= N; i++){
		if (!visited[i]) dfs(i);
	}
	reverse(order.begin(), order.end());
	
	//debug
	/*debug << "Debug : Topological Sorted\n";
	for (auto &i: order) debug << i << ' ';
	debug << endl;*/
}

void solve(){
	cin >> N >> K;
	for (int i = 1; i <= N; i++)
		cin >> t[i];
	for (int i = 0; i < K; i++){
		int s, e; cin >> s >> e;
		graph[s].push_back(e);
		parents[e].push_back(s);
	}
	int target; cin >> target;
	
	Tpsort();
	
	for (auto &i: order){
		int mxv = 0;
		for (auto &j: parents[i])
			if (mxv < t[j]) mxv = t[j];
		t[i] += mxv;
	}
	
	//debug << "ANSWER" << endl;
	cout << t[target] << endl;
	
}

int main(){
	cin >> T;
	for (int i = 0; i < T; i++){
		solve();
		for (int i = 0; i < 1001; i++){
			graph[i].clear();
			parents[i].clear();
			visited[i] = 0;
			t[i] = 0;
		}
		order.clear();
	}
	
}