고등학생 때 공부했던 건 다 잊어먹은건지 분명 아는건데 어떻게 푸는지 기억이 나지 않았던 문제다.
아! LCS! 아시는구나! 근데 어캐 푸는거였지?
우선 는 Longest Common Subsequence의 약자로 가장 긴 공통 부분 수열을 찾는 것이다.
착각하면 안 되는 부분은, Longest Common Substring과는 또 다른 개념이라서 꼭 연속된 부분 수열일 필요는 없다는 것이다.
예를 들어, ABCDSTRING 과 ABCPPSTRING의 Longest Common Substring은 STRING일 것이다.
그러나 우리가 구하고 싶은 는 ABCSTRING이다.
연속적일 필요는 없다는 것이 중요하다.
그럼, 를 구하기 위한 2차원 배열을 그려보자.
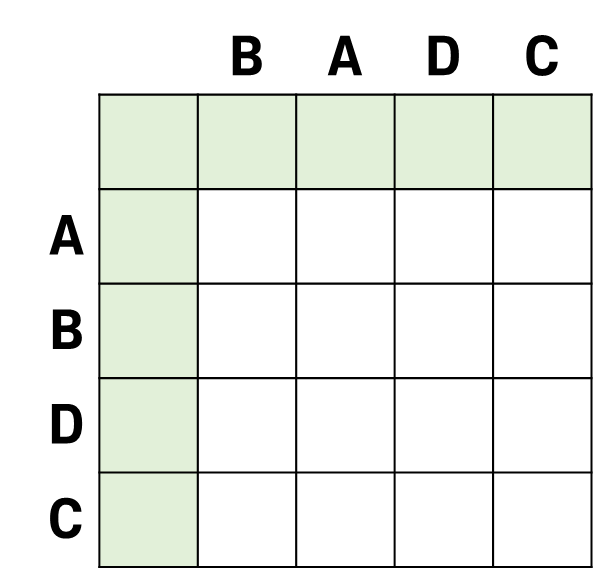
상당히 익숙한 느낌의 표가 등장했다.
가장 외곽부터 이고, 아래로 내려갈 수록 이 되고, 오른쪽으로 갈수록 이 된다.
초록색으로 칠해진 부분은 초기값인 0에서 갱신될 일이 없기 때문에 채워넣도록 하겠다.
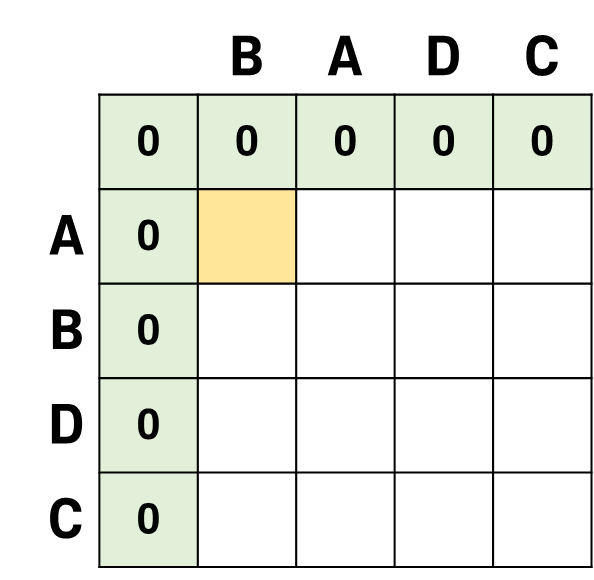
이제 부터 보자.
의 핵심은 지금 검사하고 있는 두 문자가 같을 때와 아닐 때를 구분해서 처리해주는 것이다.
지금은 을 보고 있기 때문에 B와 A를 검사하고 있으니 두 문자는 다르다.
이 때는 이전에 구한 LCS의 길이 중 더 큰 것을 가져오면 되겠다.
이 되는 것이다.
이해가 되지 않는다면 조금 진행한 후에 다시 보자.
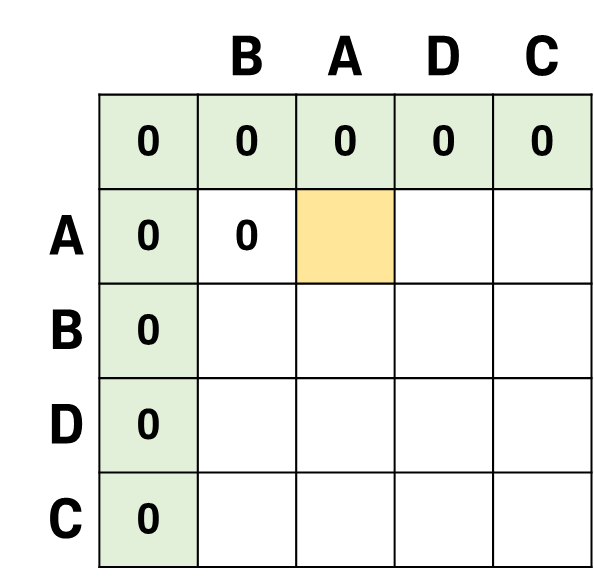
이제 를 구할 차례다.
이번에는 대상 문자인 와 가 같은 경우이다.
를 구하는 것은 와 의 를 구하는 문제와 같게 취급할 수 있다.
그러므로 ' '와 를 비교했을 때 나온 의 길이에서 1을 더한 것과 같다.

이렇게 칸 두 개를 구했을 때 나온 두 가지의 경우가 를 구하기 위해 필요한 경우의 전부다.
여기까지의 설명은 나중에 내가 혹여나 이걸 잊어버렸을 때를 대비해서 기억을 되살리기 위한 경우에 찾아보기 위한 것이고, 에 대해 처음 보는 사람을 위해 설명해놓은 것은 아니다.
조금 더 알아보기 쉬운 예제로 넘어가자.
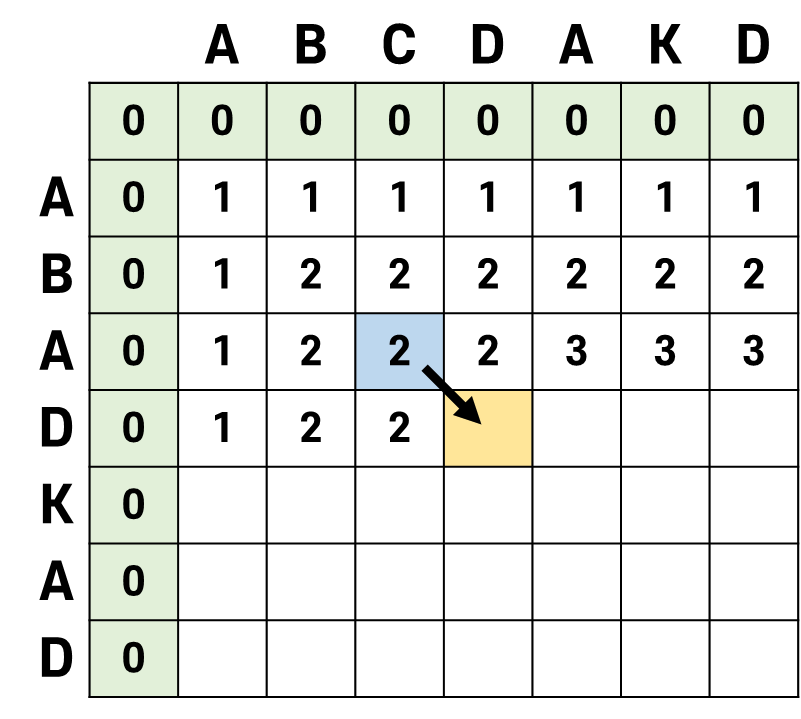
저 노란색 칸을 구해보도록 하자.
앞서 설명했듯, 저 표를 채우는 데 있어서 딱 두가지의 경우가 있다.
행에 해당하는 문자를 , 열에 해당하는 문자를 라고 해보자. (여기서 는 D이고, 는 D이다)
그 두 가지 경우는 와 가 같은 경우, 와 가 다른 경우이다.
여기서는 두 문자가 같으므로 첫 번째 경우이다.
일단 저 노란 칸을 구한다는 것은 와 의 LCS 길이를 구하는 문제와 같다.
왜 그런가는 저 표의 가장 오른쪽 아래 칸을 구하는 것이 와 의 LCS 길이를 구하기 위함이라는 것을 생각해 보자.
두 문자가 같으므로 결국 와 의 LCS 길이를 알고 있다면 그 길이에 +1한 값이 노란 칸의 값이 된다.
그렇기 때문에 의 값은 의 값에 1을 더한 것과 같다.
따라서 노란 칸에는 3이 들어간다.
일 때, 이다.
첫 번째 경우는 이렇게 간단하게 해결된다.
이제 두 번째 경우를 보자.
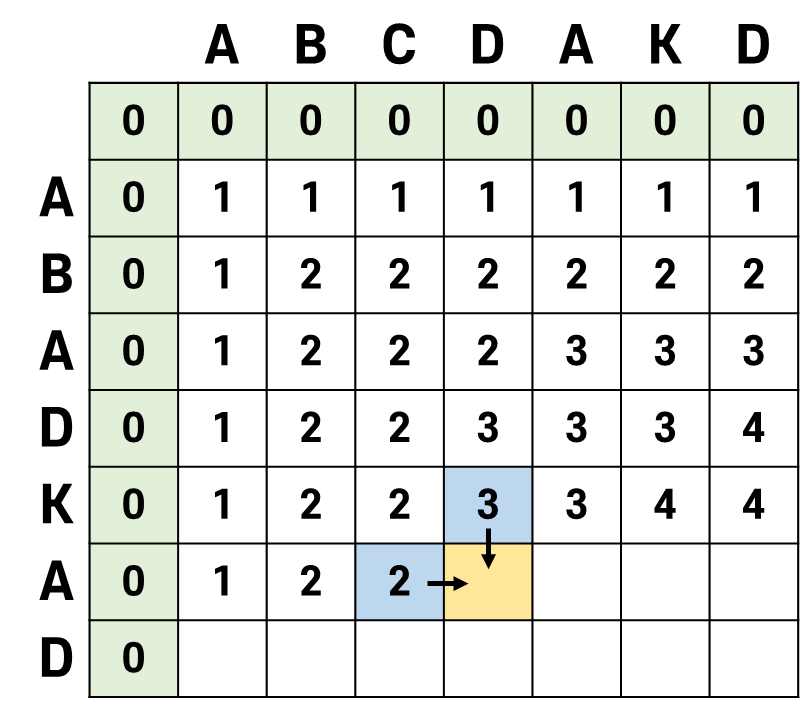
는 A, 는 D이므로 두 문자가 서로 다르다.
노란 칸을 구하는 것은 와 의 LCS 길이를 구하는 것과 같다.
이 때, 와 의 길이,
와 의 길이 중 하나에서 노란 칸의 값이 나오게 된다.
잘 모르겠다면 와 로 바꿔서 직접 구해보자.
와 에서 값을 가져올 때는 가 추가되었을 때 가 완성되어 가 바뀌는 것을 감지하지 못하는 일이 벌어진다. 이 경우, LCS 길이는 4가 되었지만 3을 가져오게 된다.
그러나 와 에서 값을 가져올 때는 아무 문제 없이 가져올 수 있다. 이 때 LCS 길이 4를 가져온다.
두 경우 모두에서 LCS가 갱신되는 일은 없고, 많아도 하나의 경우에서만 LCS가 갱신된다.
그러나 A 경우에서 일어난 LCS의 갱신은 B 경우에는 이미 반영되어 있기 때문에,
LCS가 변화하지 않은 경우에서 올바른 값을 가지고 있다.
올바른 값은 항상 올바르지 않은 값보다 크므로 두 경우 중 더 큰 값을 가져오면 된다.
표에서 보면, 구하려는 값의 위나 왼쪽 중 더 큰 값을 가져오면 된다.
이것을 식으로 나타내면, 일 때, 이다.
따라서 노란색 칸은 max(2, 3)인 3이 차지하게 될 것이다.

위 방법으로 표를 모두 채운 결과이다.
가장 오른쪽 아래 칸이 와 의 LCS 길이가 된다.
역추적을 통해 LCS를 구해보자.
LCS의 길이가 증가하는 경우는 단 하나다.
바로 검사하는 두 문자가 같은 경우다.
이 경우에만 현재 길이보다 작은 칸으로 이동할 수 있고, result 문자열에 문자가 더해지게 된다.
이러한 경우를 찾기 위해서 같은 길이를 가진 칸으로 이동하면서 탐색을 하면 된다.
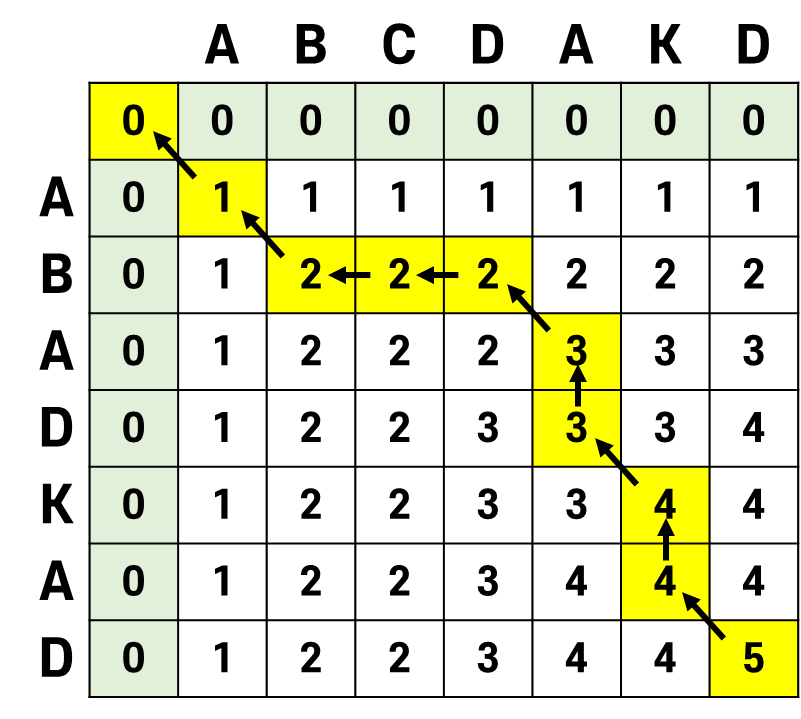
노란색은 탐색 경로이다. 생각했던 역추적 경로와 같은지 확인해보자.
물론 위 문자열은 ABAKD 말고도 ABDKD라는 길이가 같은 또 다른 가 있으므로 다른 탐색 경로가 더 있다.
위 규칙에 부합하면서 잘 움직였는지만 확인해보자.
코드
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
constexpr bool local = true;
#else
constexpr bool local = false;
#endif
#define FASTIO ios_base::sync_with_stdio;cin.tie(nullptr);cout.tie(nullptr);
#define debug if constexpr (local) std::cout
#define endl '\n'
int board[1001][1001];
string LCS(string x, string y){
x = ' ' + x;
y = ' ' + y;
for (int i = 1; i < x.length(); i++){ //LCS Board
for (int j = 1; j < y.length(); j++){
if (x[i] == y[j])
board[i][j] = board[i-1][j-1] + 1;
else
board[i][j] = max(board[i-1][j], board[i][j-1]);
}
}
debug << x << ' ' << y << endl;
for (int i = 1; i < x.length(); i++){ //LCS Board
for (int j = 1; j < y.length(); j++){
debug << board[i][j] << ' ';
} debug << endl;
}
// find LCS
int px = x.length()-1;
int py = y.length()-1;
string result;
while (board[px][py] != 0){
if (x[px] == y[py]){ // downgrade
result = x[px] + result;
px--; py--;
}
else{
if (board[px-1][py] > board[px][py-1]){
px--;
}
else py--;
}
}
return result;
}
int main(){
string a, b;
cin >> a >> b;
string r = LCS(a, b);
debug << r << endl;
cout << r.length();
}