Linear 분류
이미지 x가 (이미지 크기x채널수)크기의 열 벡터로 바뀌어 w와 만나서 각 클래스에 대한 점수를 나타내는 클래스 갯수만큼의 숫자를 출력
위의 그림을 보면 3개의 이미지에 대해, 특정 W값을 통해 예측된 클래스 점수가 나타남
여기서 우리는 해당 정답 클래스의 점수가 가장 높기를 원하면서, 동시에 손실함수가 최소가 되길 원함 => 선형 분류가 잘되었다
Linear분류 평가 척도
손실함수가 최소화되는 파라미터를 찾아야함
=> 손실함수는 해당 분류기가 얼마나 좋은지 알려주는 척도
Linear분류에서 해야 할 것
- 손실 함수를 정의하여 학습 데이터 전체에 결쳐 특정 W에 대한 나쁨의 정도를 정량화
- 손실 함수를 최소화하는 파라미터 찾는 방법 생각
N개의 예제, x는 이미지 픽셀 값, y는 label
f = 이미지를 통해 나오는 예측 레이블
Li = f와 실제 label값을 통해 계산할 손실 함수
L = 데이터셋 N개의 손실들의 평균
손실함수 유형
1. Multiclass SVM Loss
yi가 정답인 카테고리만 빼고 모든 카테고리 y에 대해 하나하나 비교하여 손실을 구함
0과 어떤 값 중에 최대값을 취하는 스타일의 손실함수는 위와 같은 힌지손실(hinge loss)스타일을 가짐
x축 = S_yi(정답 클래스 점수), y축 = 손실
=> 정답 클래스 점수가 증가하면, margin에 다다를 때까지 손실은 선형으로 줄어들다가 0이 됨
cat 클래스에 대한 손실값
최종적으로 5.27만큼의 손실 발생 => 해당 분류기에 성능에 대한 정량적 측정값
Q1. 손실의 최소/최대값?
최소 손실은 모든 클래스에 정답 점수가 크다면 손실값은 0
최대 손실은 정답 점수가 매우 큰 음수로 간다면 손실값은 무한대
Q2. 자동차 점수가 조금 바뀐다면 손실에 어떤 일이 벌어지나?
자동차 클래스의 정답 점수가 꽤 크다면 손실은 변하지 않는다.
SVM Loss는 정답 클래스 점수가 틀린 점수보다 1 이상 큰지에 관심
자동차 클래스 정답 점수가 다른 점수보다 꽤 크다면 여전히 1 이상 마진이 남는다.
2. SoftMax Loss
Multiclass SVM Loss는 점수에 대해 해석을 하지않고, 정답 클래스의 점수가 틀린 클래스보다 크기만 하면 됨
SoftMax Loss는 점수에 대해 지수화하여 양수로 만들고 이를 정규화하여 확률 분포를 얻음
=> 정답 클래스에 대한 확률이 1에 가까워지는 w를 찾는 것이 목표
SoftMax Loss = 정답 클래스의 음수 로그
=> 0.89만큼의 손실 발생 => 해당 분류기에 성능에 대한 정량적 측정값
Q1. 손실의 최소/최대값?
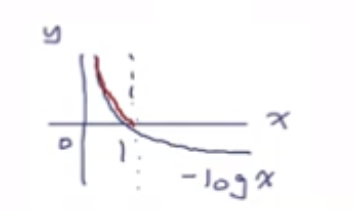최소 손실은 모든 클래스에 정답 점수가 1의 값을 갖는다면 -log(1) = 0이 되어 손실값은 0
그러나 지수화, 정규화를 갖고 있기에 1의 확률을 갖는것은 불가능하고, 유한한 정밀도만 갖음
최대 손실은 모든 클래스에 정답 점수가 0의 값을 갖는다면 -log(0) = 양의 무한대가 되어 손실값은 양의 무한대
그러나 지수화, 정규화를 갖고 있기에 0의 확률을 갖는것은 불가능하고, 유한한 정밀도만 갖음
Q2. 자동차 점수가 조금 바뀐다면 손실에 어떤 일이 벌어지나?
바뀐 점수가 그대로 확률값에 적용되므로 손실에도 변화가 생긴다
SVM Loss와 비교해보면 softmax가 데이터에 민감하다
Optimization
Loss가 최소화되는 지점을 찾아나가는 것
전략 #1 Random search
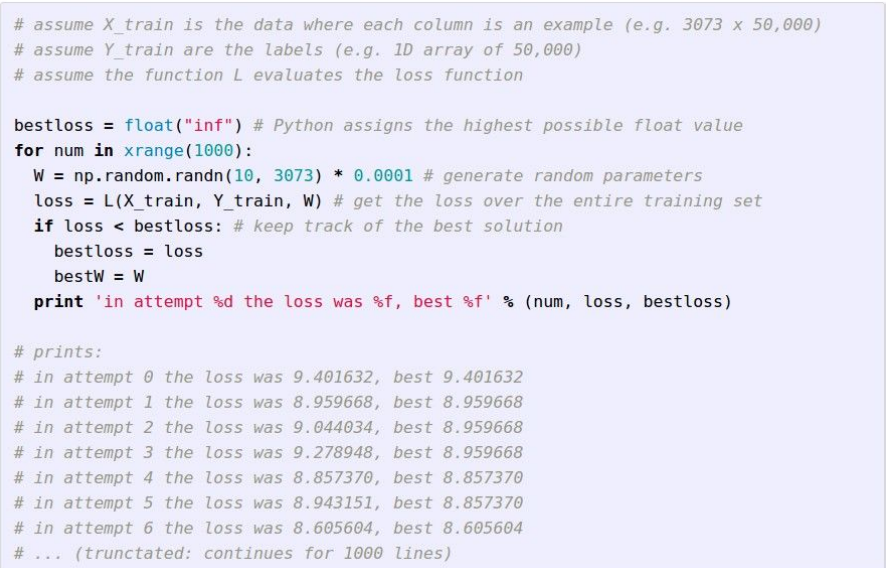
W를 임의 샘플링하고, 모든 Loss를 계산하여 어떤 W가 좋은지 판단
전략 #2 Gradient Descent(경사 하강법)
loss함수를 최소값이 있는 오목한 함수라고 생각할 때,
각 지점에서 미분하여 구한 기울기가 더 작은 점이 찾으려고 하는 최소 loss를 갖는 최종 W와 더 가까운 점이라 판단
=> W Gradient Descent가 증가하는 반대방향으로 움직임
- weight_grad : gradient를 계산한 결과값
- step_size : 한번의 step에서 이동할 거리
step_size가 높으면 최적의 W까지 더 적은 회숫의 step만으로도 도달 가능하지만,최적의 W를 지나쳐버리는 overshoot 문제가 발생할 수 있고,
step_size가 너무 낮으면 정교하지만 오래 걸린다는 단점 - step_size앞에 -가 붙는 이유: 그래프가 음의 기울기면 기울기가 0인 지점으로 가려면 +방향으로 가야하고, 양의 기울기면 기울기가 0인 지점으로 가려면 -방향으로 가야한다.
즉, 반대방향으로 가기에 -를 붙여준다
Stochastic Gradient Descent(확률적 경사하강법)
GD방법은 모든 데이터를 이용하여 계산하기 때문에 느리다는 단점
SGD는 매 학습마다 한 개의 샘플을 무작위로 선택하고 그 샘플에 대한 gradient를 계산
SGD 한계
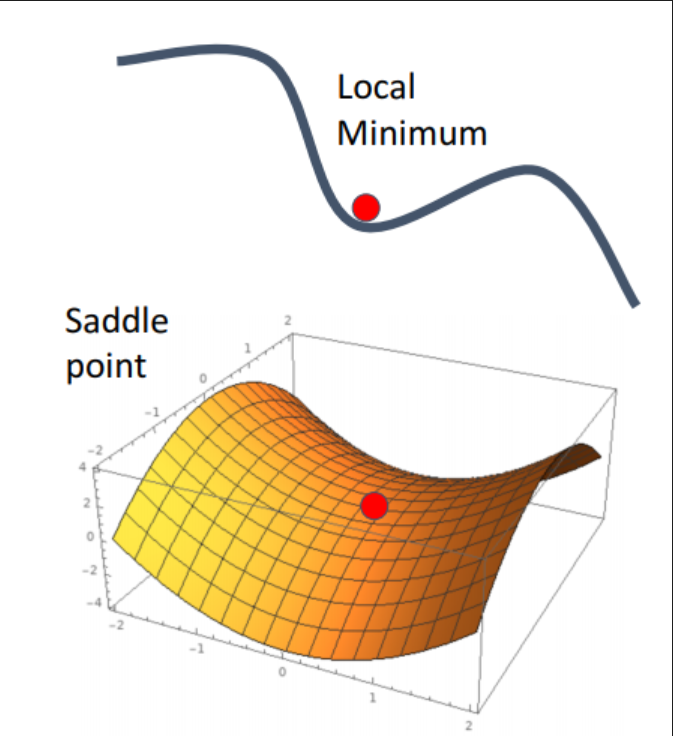
- Loss함수에 local minimum값이 있는 경우?
local minimum에서도 gradient는 0이므로 경사하강이 고착됨
함수가 고차원이고 복잡한 경우에 gradient가 0인 saddle point에 위치해서 학습이 크게 지연될 수 있음
(*saddle point : 한쪽 방향으로는 상승하고, 다른 방향으로 감소하는 형태 )
SGD의 한계를 보완하기 위한 다양한 Optimizer들이 존재
이는 1차 세미나에서 확인 가능함
