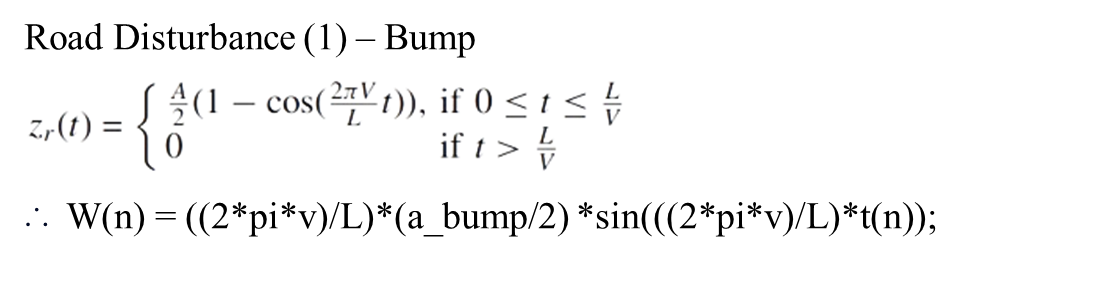
저번 포스트에 이어서 이번에는 세 가지 도로 환경 위에서 Active Suspension이 얼마나 안정적으로 작동하는 지 확인을 할 것인데, 이번에는 Observer(Filter)을 함께 구성하여 관찰할 예정이다.
Observer의 경우, 상태를 정확하게 알 수 없거나, 측정이 불가한 State variable을 estimator을 통해 추정하고, 추정값과 실제값 차이의 error을 줄이도록 만든다. 따라서 Observer의 pole을 잘 설계하는 것과 더불어 이것이 추정값과 어느정도의 오차를 가지는지 파악해볼 필요가 있다.
Design the Active Suspension with Simulink
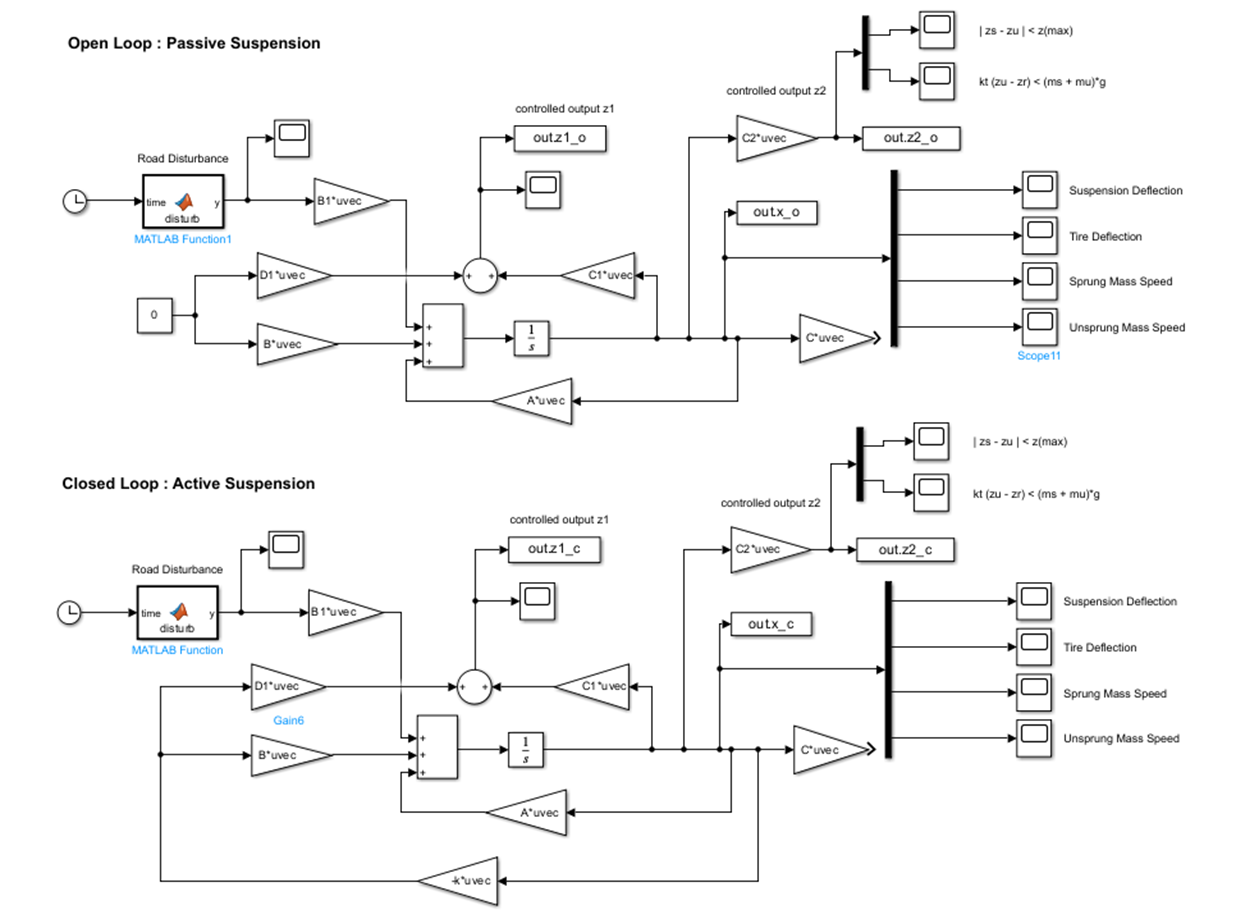
< Without Observer > - Open loop and Closed loop sys
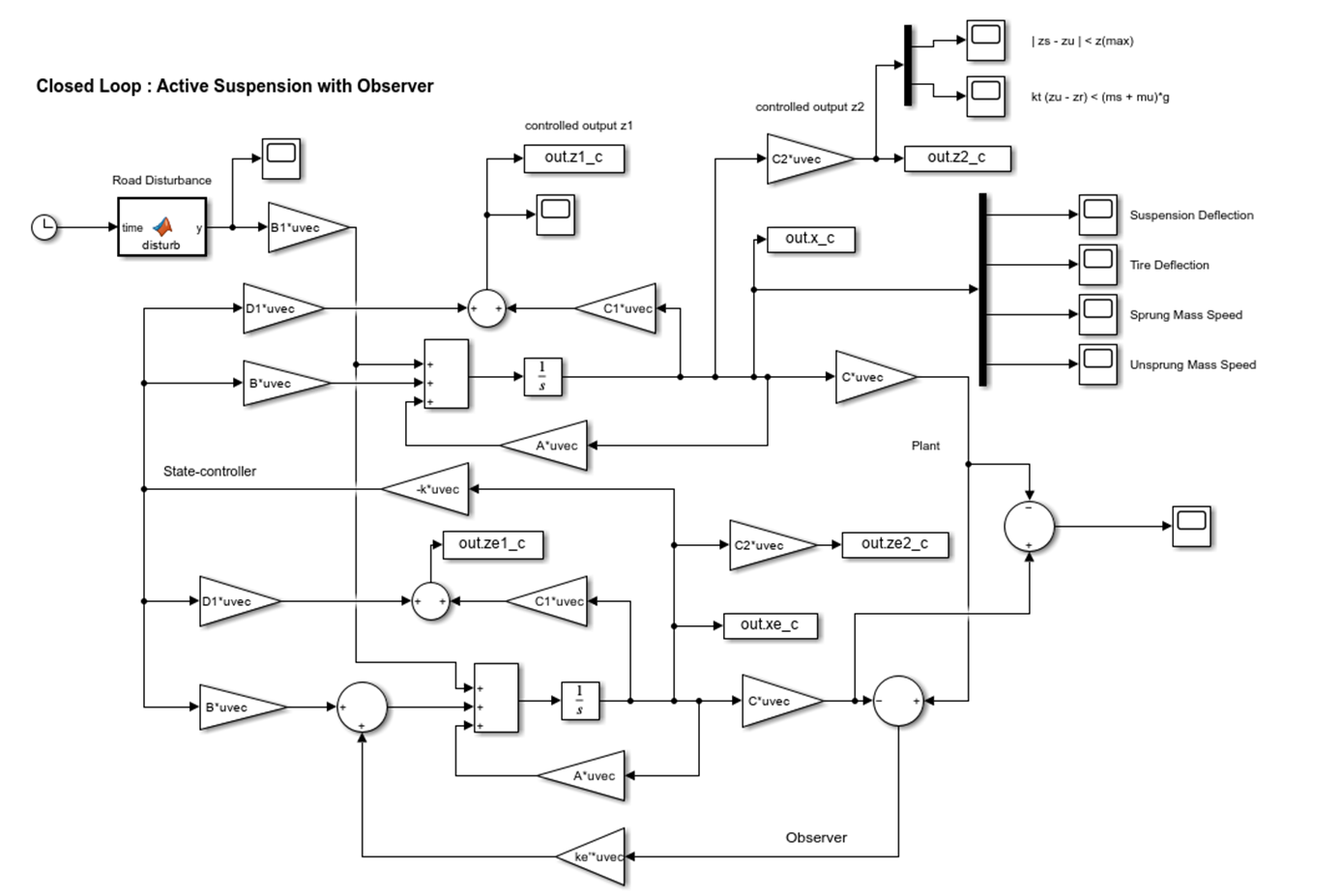
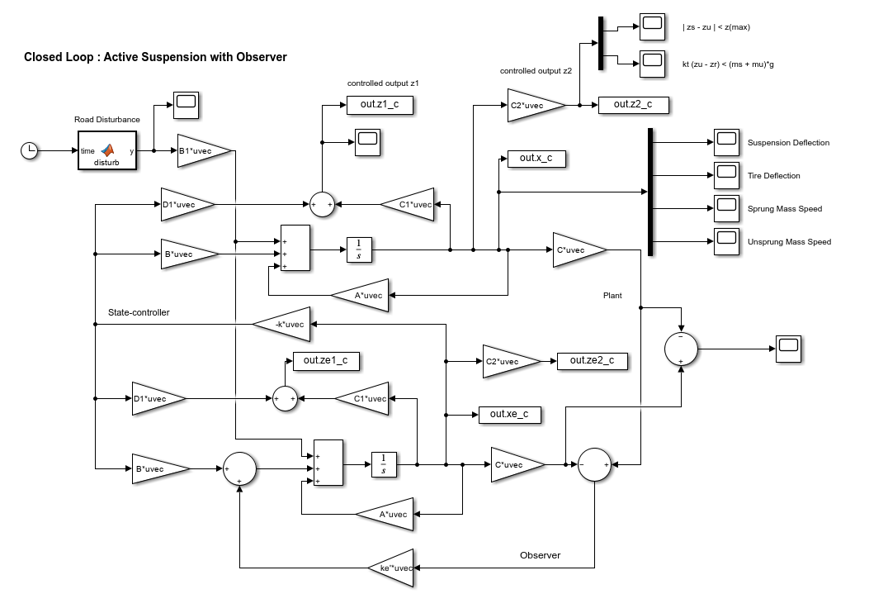
< with Observer >
시스템을 보면, 위의 Observer의 경우 아래의 Closed loop에 구현이 되어 있음을 확인할 수 있다. 상태를 추정하는 State-estimator의 u=-kx와 함께 ke'를 두어 나타내어있다. 또한 각각의 State variable X1~X4와 Controlled output z1, z2는 Scope를 통해 확인해보며 진행을 하고, Error값은 추정값과 실제값의 차이를 구해 확인한다.
이를 MATLAB 코드로 구현하여 결과를 확인해보면 다음과 같다.
.
MATLAB Code for Active Suspension with Observer

앞에서 사용하였던 k 값과, 이보다 더 빠르게 수렴하도록 임의로 설정한 observer의 desired pole값이다. 본 시뮬레이션에서는 각 desired pole을 구하여 가장 최적이 되는 값을 찾을 수 있도록 하였으며, 이는 그래프로 수렴하는 속도, Mp 등 여러 complex plane의 지표로 확인할 수 있다.
이제, 다음과 같은 세 가지 도로 환경에서의 Active suspension의 성능을 test 해보자.
[1] Bump
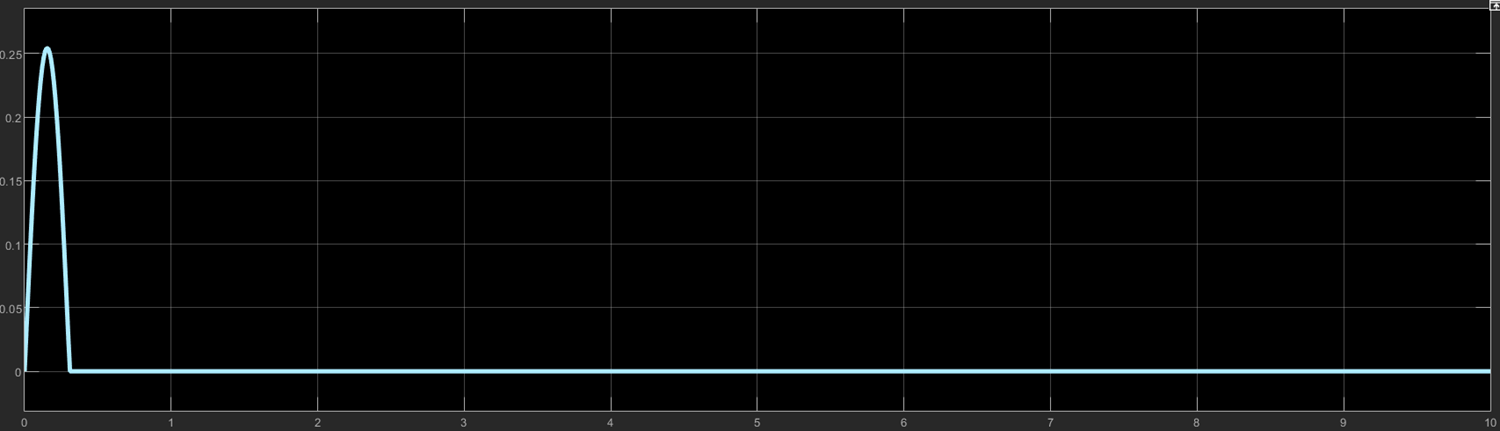
우선 Simulink에서 X값과 추정값 Xe를 추출하고, 이에 대한 Error을 정의한다.
%% Function for the steady-state
X0=[0;0;0;0];
Xe0=[1e-03;1e-03;1e-03;1e-03];
out = sim('suspension_simul.slx',10);
Time=out.x_c.time;
% Define variable X from simulink
X_o=out.x_o.signals.values;
X_c=out.x_c.signals.values;
Xe=out.xe_c.signals.values;
%Define variable Z1,Z2 from simulink
Z1_o=out.z1_o.signals.values;
Z1_c=out.z1_c.signals.values;
Ze1=out.ze1_c.signals.values;
Z2_o=out.z2_o.signals.values;
Z2_c=out.z2_c.signals.values;
Ze2=out.ze2_c.signals.values;
Error=X_c-Xe;이를 그래프로 나타내면, 다음과 같다.
Xe0=[1e-02 1e-02 1e-02 1e-02]
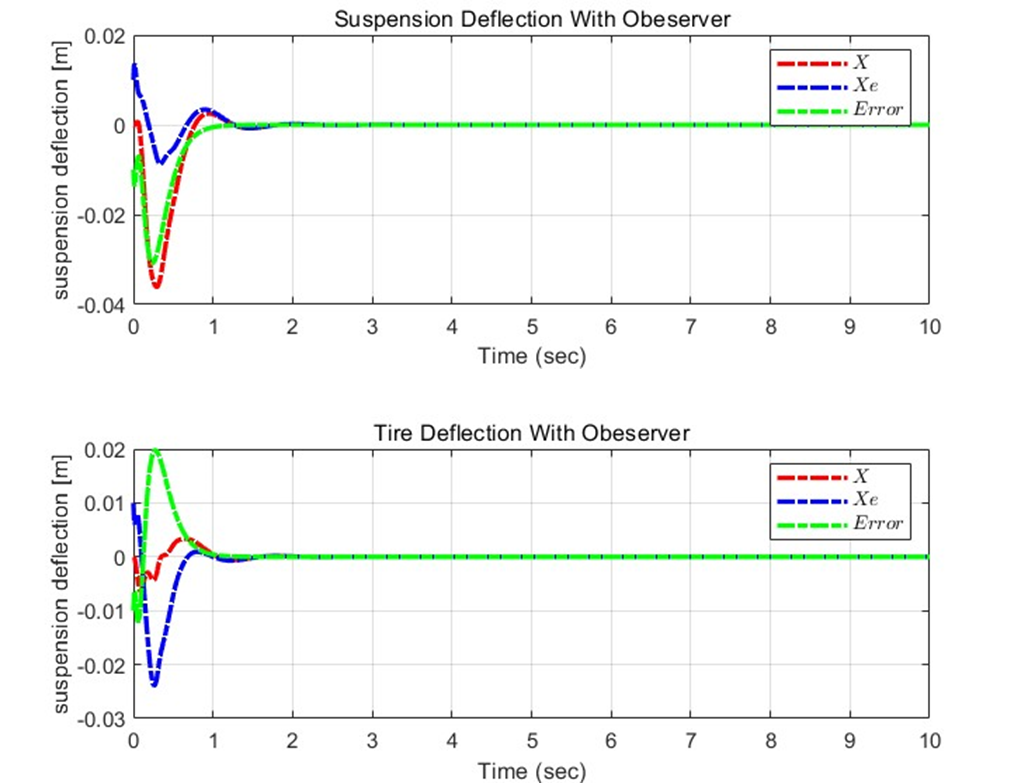

이를 보면, 실제 X값과 추정값 Xe사이의 Error이 Observer의 초기값의 영향을 받아 발생하는 것을 확인할 수 있고, 빠른 시간 내에 0으로 수렴하는 것을 볼 수 있다. Observer의 초기값을 실제 초기값과 더 유사하게 근접시키면 그래프 양상은 다음과 같이 도출된다.
Xe0=[1e-03 1e-03 1e-03 1e-03]
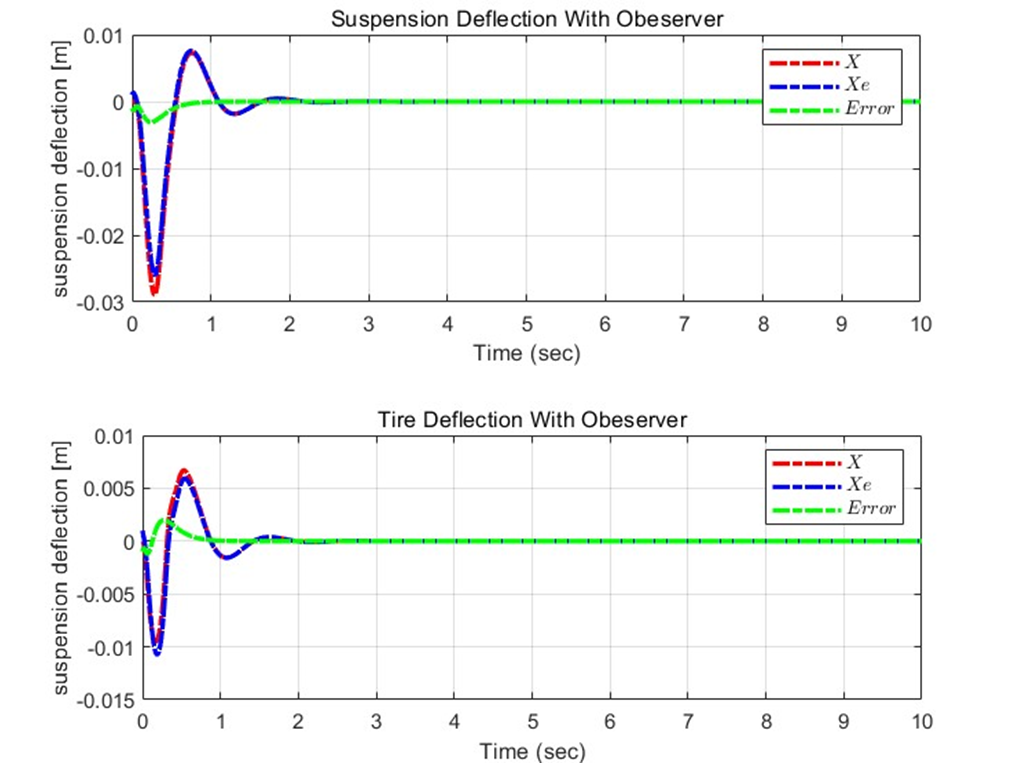
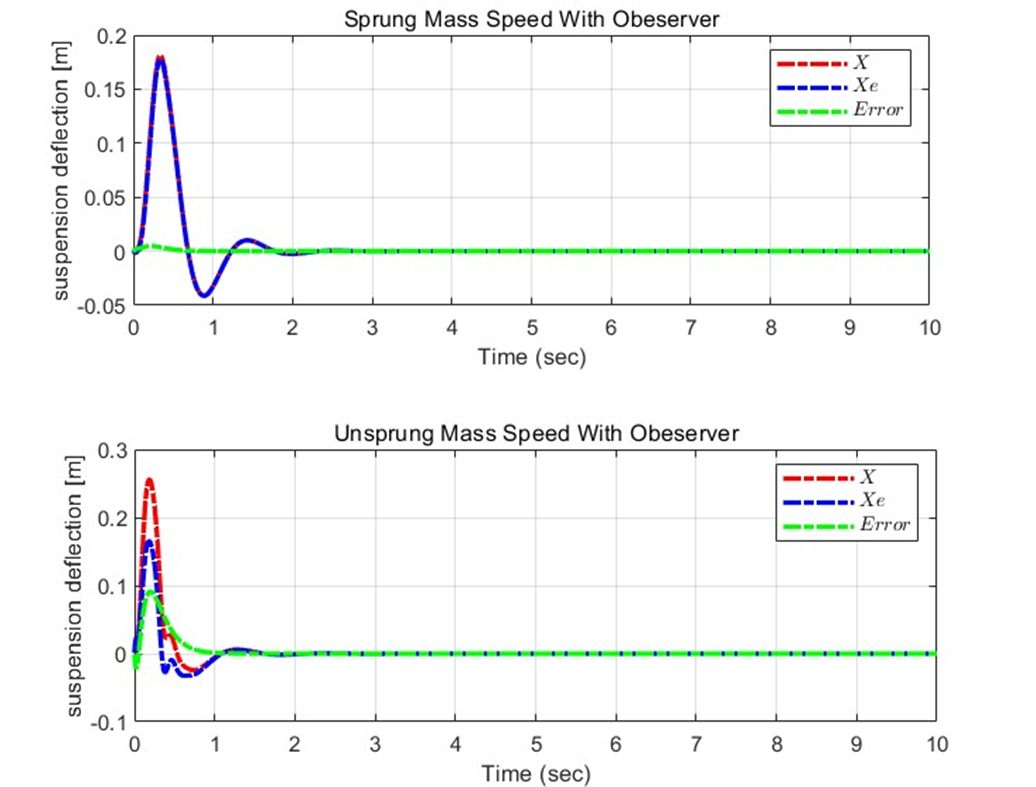
실제로 Observer을 추가한 Active Suspension의 성능 결과도 plot해보자.
# Define the function
open = @(X1,n) A*X1+B*u+B1*W(:,n);
closed = @(X2,n) (A-B*k)*X2+B1*W(:,n);
observed = @(X3,n) (A-B*k-ke'*C)*X3;
# Use Runge-Kutta 4th method for these three functions respectively
...Simulation (Plot) – Open loop and Closed loop for X1~X4
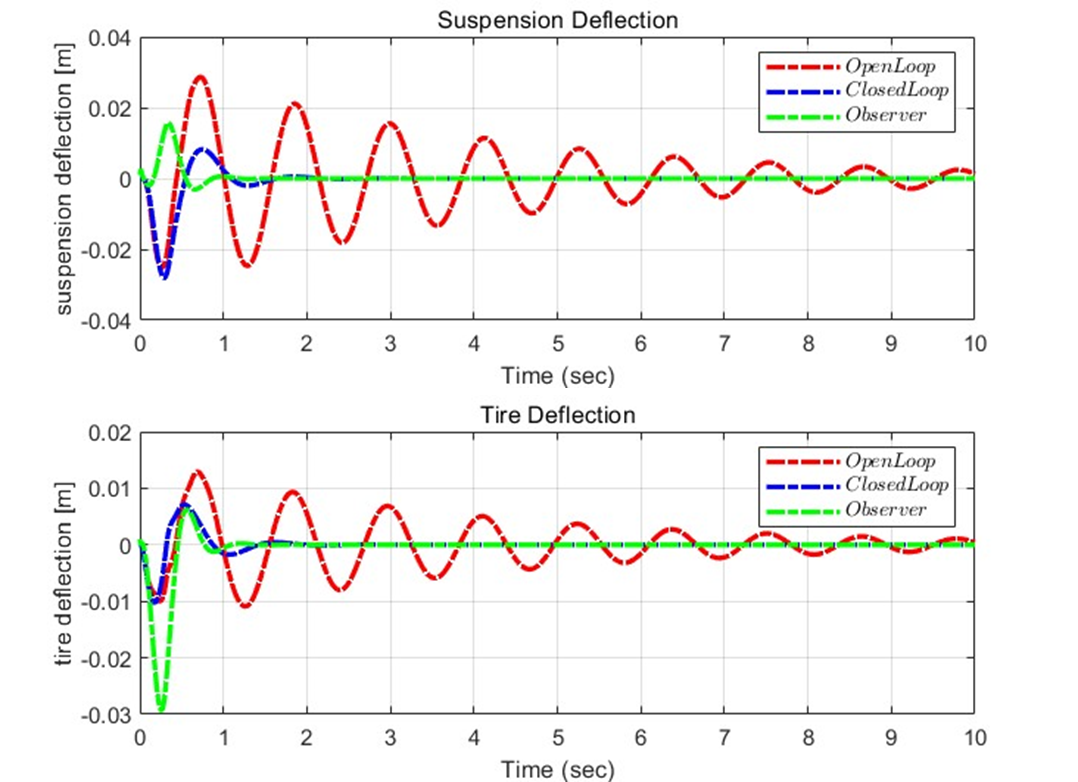
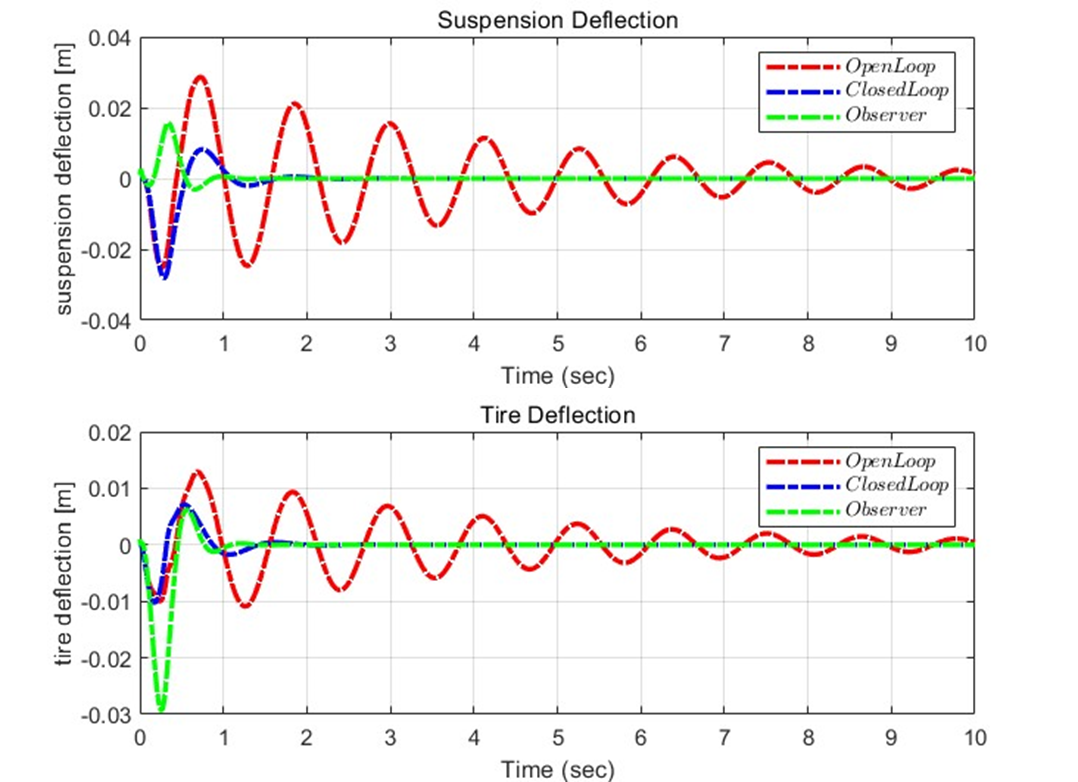
이를 보면, Bump를 지났을 때 Observer의 경우 빠르게 안정화하는 것을 볼 수 있다. 위의 X와 Xe의 차이를 통해 보았던 것과 같이, 초기값 차이에 따른 Error이 발생하지만 이내 Simulation 시작 후 1초경에 안정화되는 것을 확인할 수 있다.
도로의 상황을 변화시켜, 동일한 과정을 관찰해보자.
[2] Rough Road
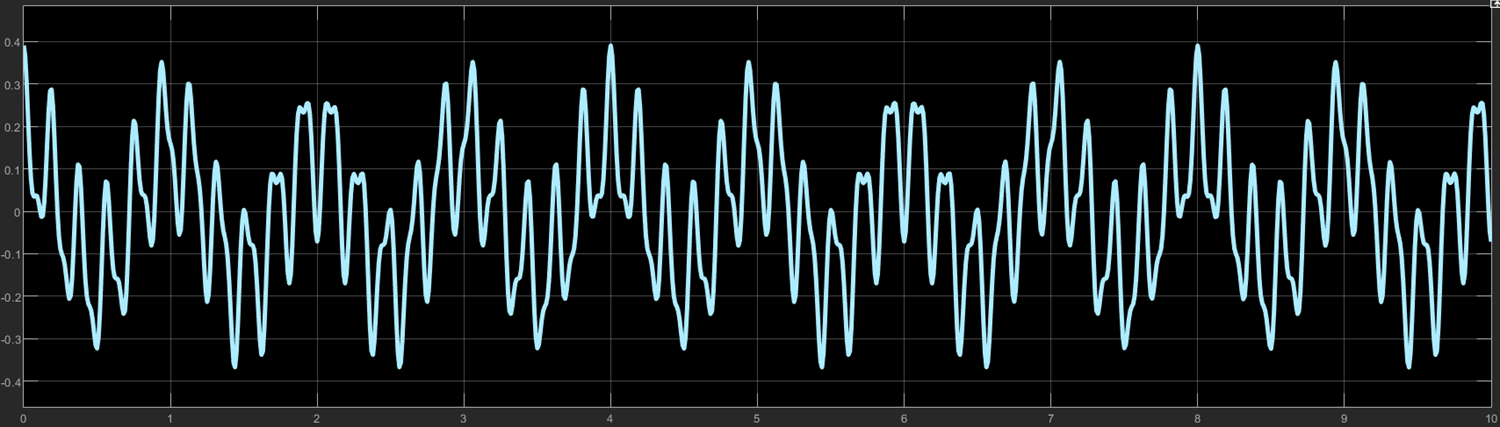
Road Disturbance를 위해 울퉁불퉁한 도포 표면을 다음과 같이 수학적으로 모델링하여 시뮬레이션을 진행한다.
우선, Simulink에서 X와 추정값인 Xe를 추출하여 그 차이인 Error을 plot하여 관찰한다.
Initial value of observer [1e-02;1e-02;1e-02;1e-02];
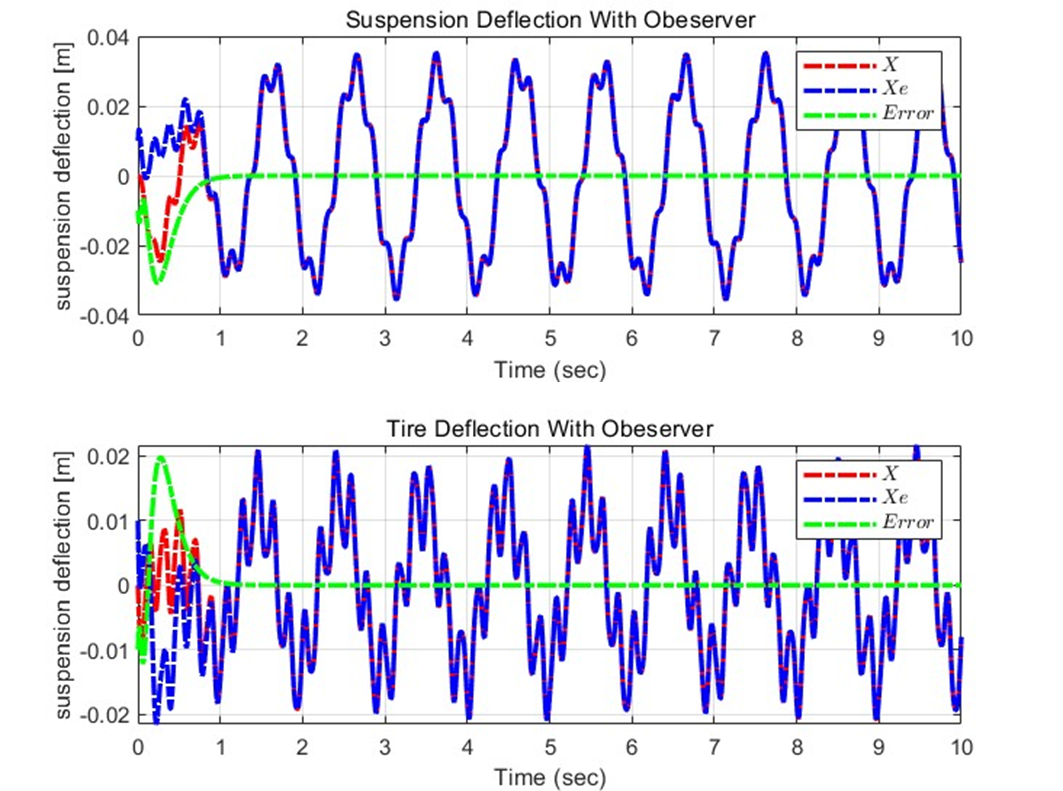
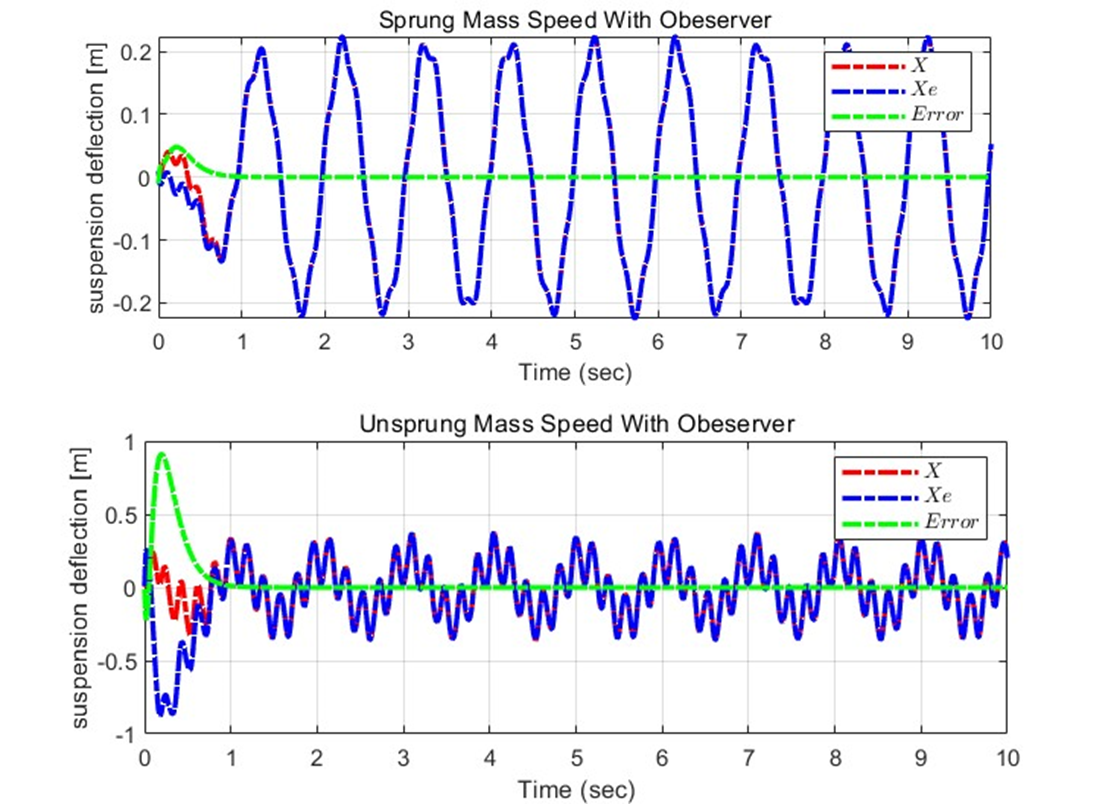
이 역시 관찰해보면, 초기값의 차이에 따라 X와 Xe값 사이에 초기 Error가 발생하고, 이는 초록색 plot을 보면 확인할 수 있다. 그러나 시간이 지남에 따라 빠르게 수렴하여 Error이 0이 되는 것을 확인할 수 있고, Observer이 잘 작동하고 있음을 확인할 수 있다.
이에 대해 Observer이 결합된 X 결과값에 대해 관찰해보자.
Simulation (Plot) – Open loop and Closed loop for X1~X4
Initial value of observer [1e-02;1e-02;1e-02;1e-02];


위 그래프를 보면, Open loop에 비해 파란색으로 표시된 Closed loop가 rough road에 대해 더 안정적으로 주행하는 것을 볼 수 있다. 또한, Observer이 초록색으로 초기 Error 이후 빠르게 오류가 0으로 수렴하는 것을 관찰할 수 있다.
[3] Random Response
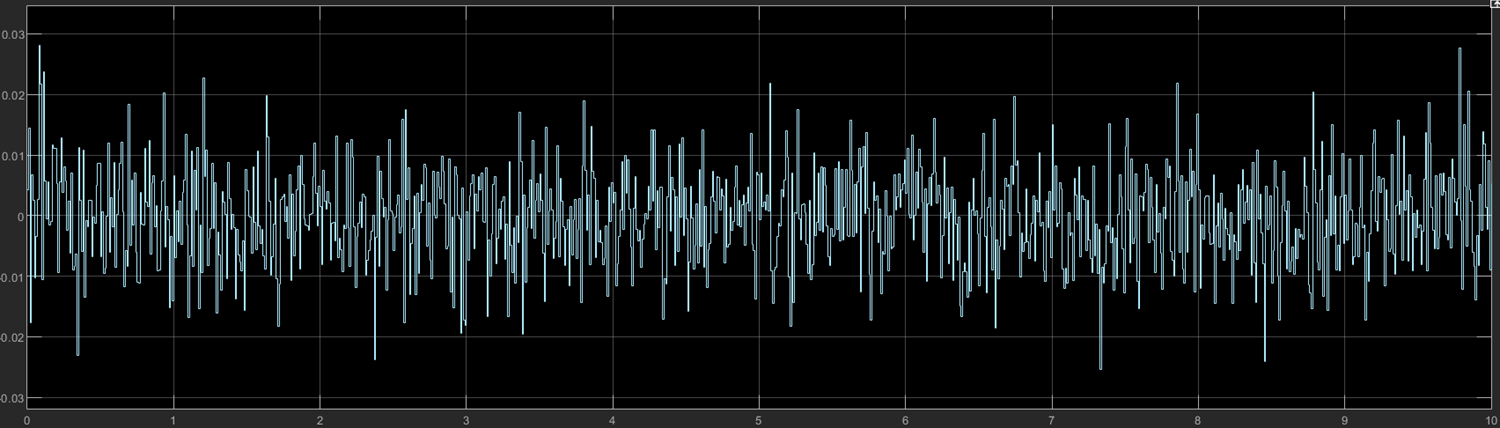
도로 표면의 random으로 발생하는 장애물을 gaussian 분포를 이용해 modeling하고, 도로에 대한 평가도를 grade로 나타내어 random 도로를 설계한다.
우선 Simulink에서 X와 추정값인 Xe를 추출하여 그 차이인 Error을 plot하여 관찰한다.
Initial value of observer [1e-03;1e-03;1e-03;1e-03];
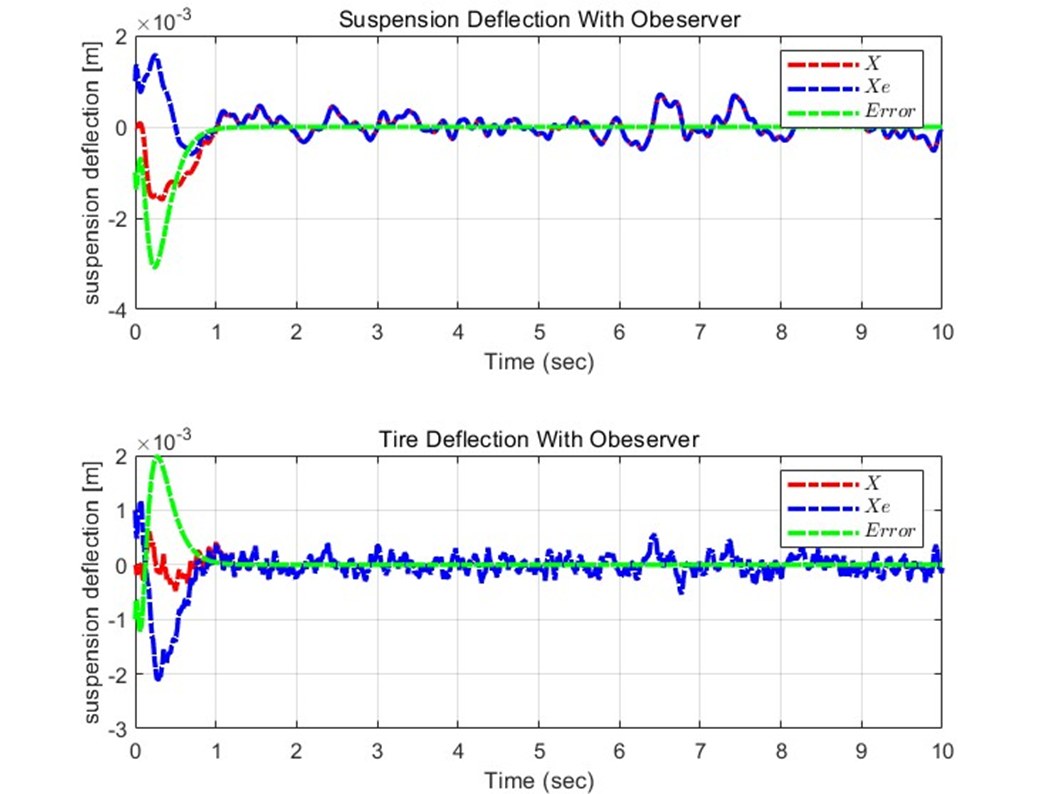

초기값의 차이에 따라 X와 Xe값 사이에 초기 Error가 발생하는 것을 볼 수 있고, 위 두 도로 상황과 동일하게 시간이 지남에 따라 빠르게 수렴하여 Error이 0이 되는 것을 확인할 수 있다.
Observer을 설계한 시스템을 비교해보면 다음과 같다.
Simulation (Plot) – Open loop and Closed loop for X1~X4

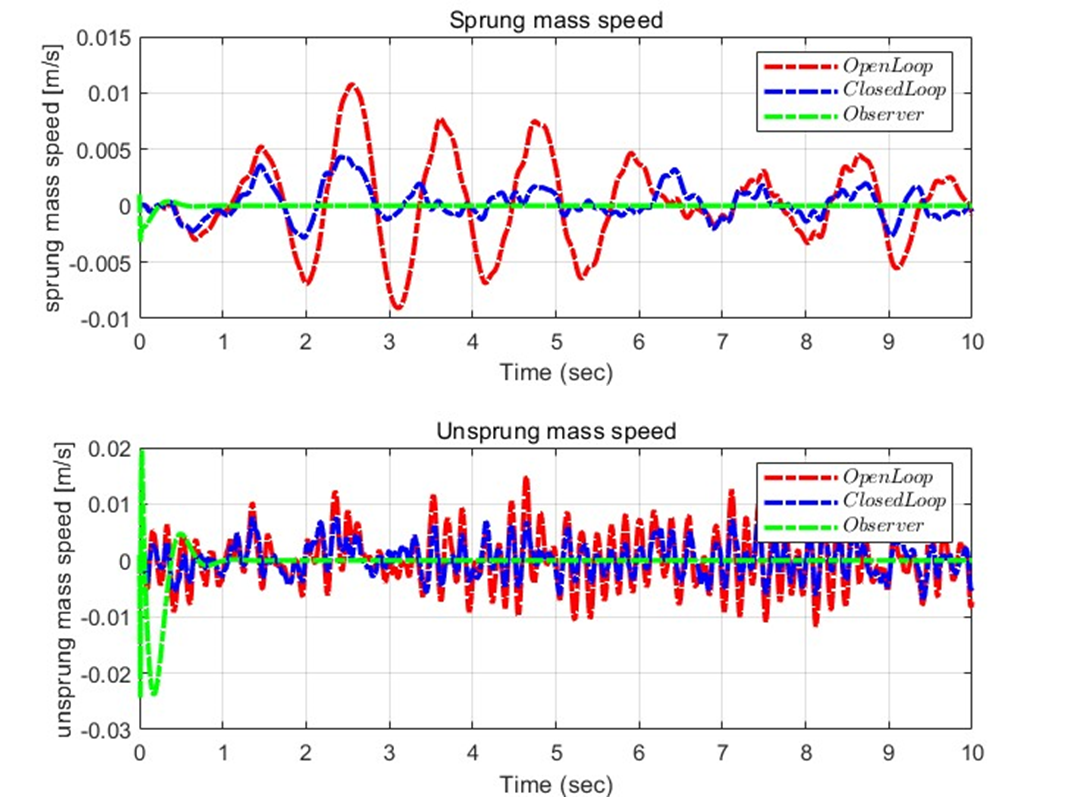
이를 통해 Random한 장애물을 가지는 도로에서도, Open loop에 비해 파란색으로 표시된 Closed loop에서 더 안정적인 suspension 작동을 하는 것을 확인할 수 있다. 또한, Observer이 표시된 초록색 plot을 보면 초기 Error 이후에 0으로 빠르게 수렴하여 Filter이 잘 설계되었다는 것을 알 수 있다.
결론적으로,
x1 = suspension deflection
x2 = tire deflection
x3 = sprung mass speed
x4 = unsprung mass speed
4가지 state-vriable을 설정하여 suspension의 성능에 대한 지표를 관찰할 수 있었고, 특히나 x1의 Suspension Deflection은 𝑧1 for sprung mass acceleration 과 깊은 관련을 가지고 있는 성분이다.
이를 이용하여 Controlled Output을 z1, z2로 선정하여 승차감 향상을 위해 Plot값을 비교하며 가장 최소화 될 수 있도록 설계하였다. 이는 Active Suspension 이 자동적으로 도로의 상황에 구애받지 않고, 기계적인 부품들을 제어할 수 있도록 하여 차량의 주행 성능을 개선시킨다.