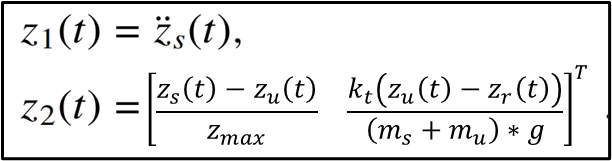
[ Fuzzy Sampled-Data Control for Uncertain Vehicle Suspension System ]
논문 참조
< Quarter Car Model >
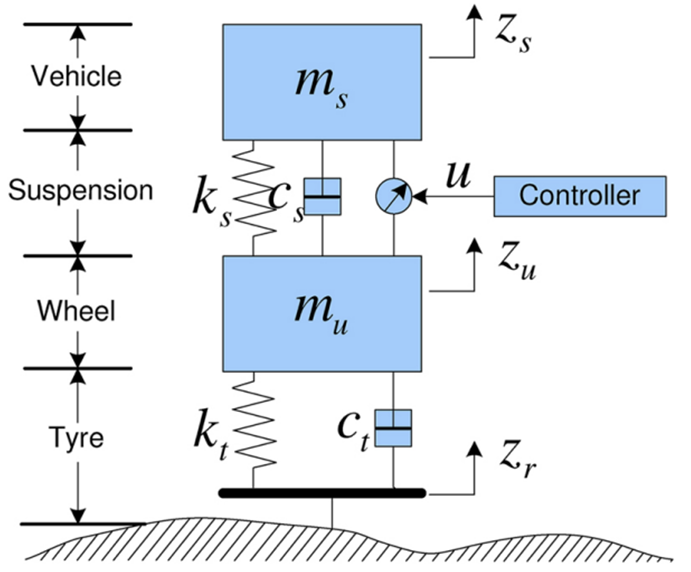

이때 우리가 사용하는 suspension의 상수값은 다음과 같이 정의한다. (논문에 따름)

이에 대해 2자유도를 가진 quarter car model 에서의 동작에 대한 물리학적인 방정식을 쓰면 다음과 같다.
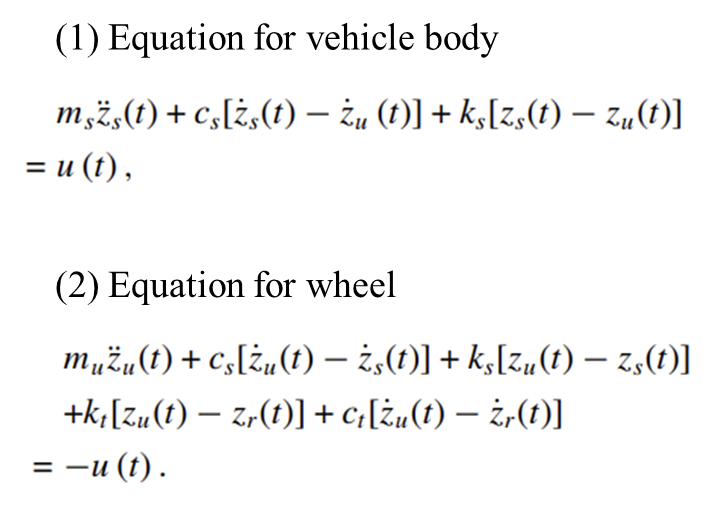
이제, 본 equation을 steady-state로 정의하여 시스템을 관찰하도록 한다. 이때 state-variable을 X1~X4로 정의하고, Controlled output Z1,Z2을 정의하여 함께 관찰하도록 한다
(1) Steady-State Model – for X
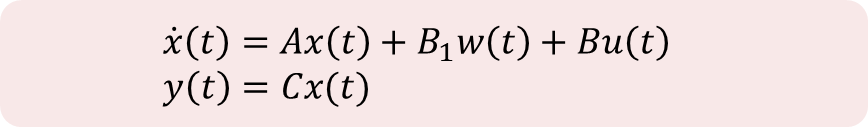
Define x1~x4 for Steady-state,
이때, Matrix A,B1,B,C는 Motion Equation에 의하여 다음과 같이 정의한다.
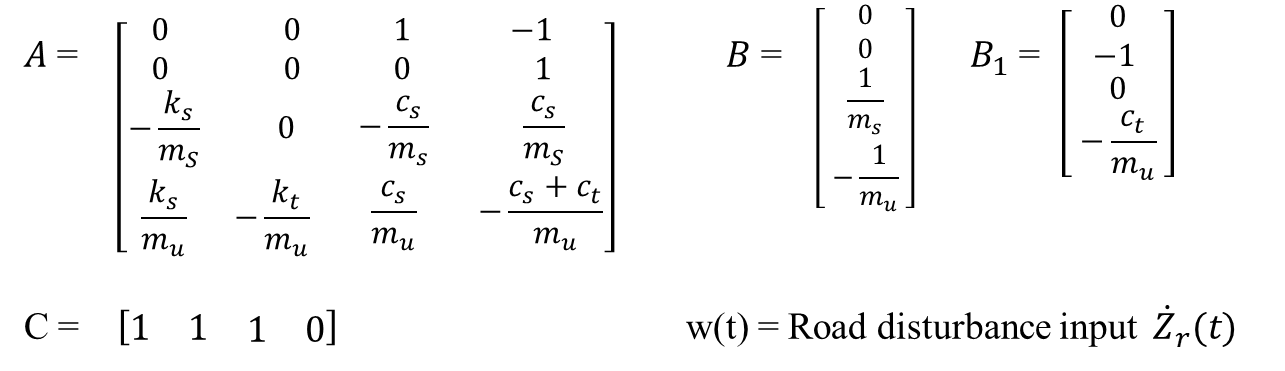
_
(2) Steady-State Model – for controlled output
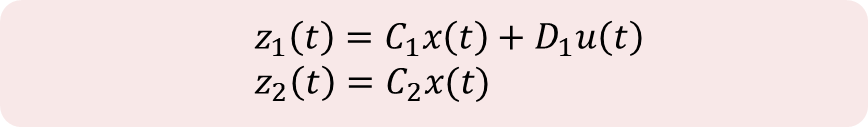
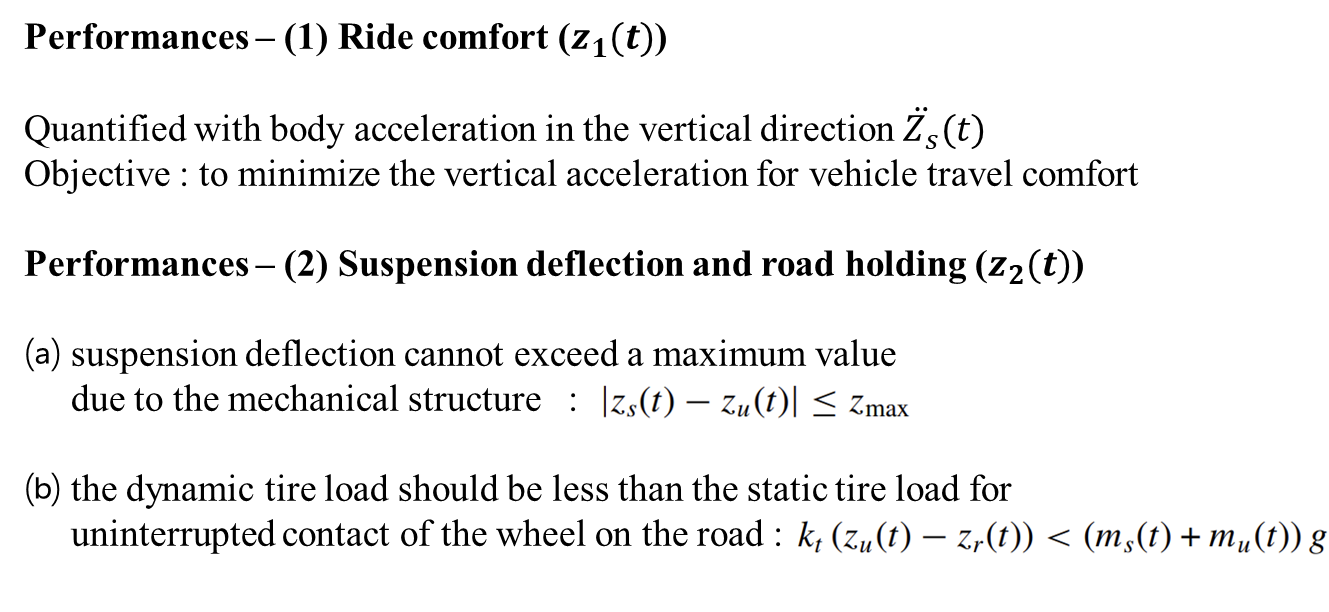
Define Z1, Z2 for Steady-state,
이때, Matrix C1, C2, D1은 다음과 같이 정의한다.
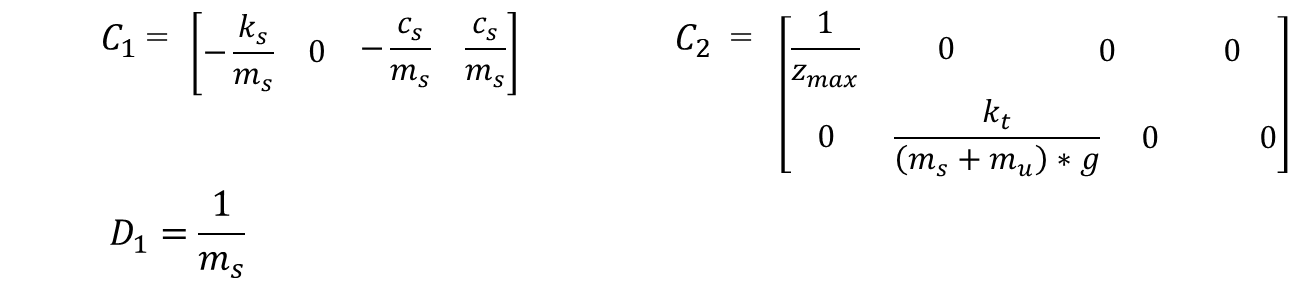
.
Simulink for Active Suspension with State-estimator
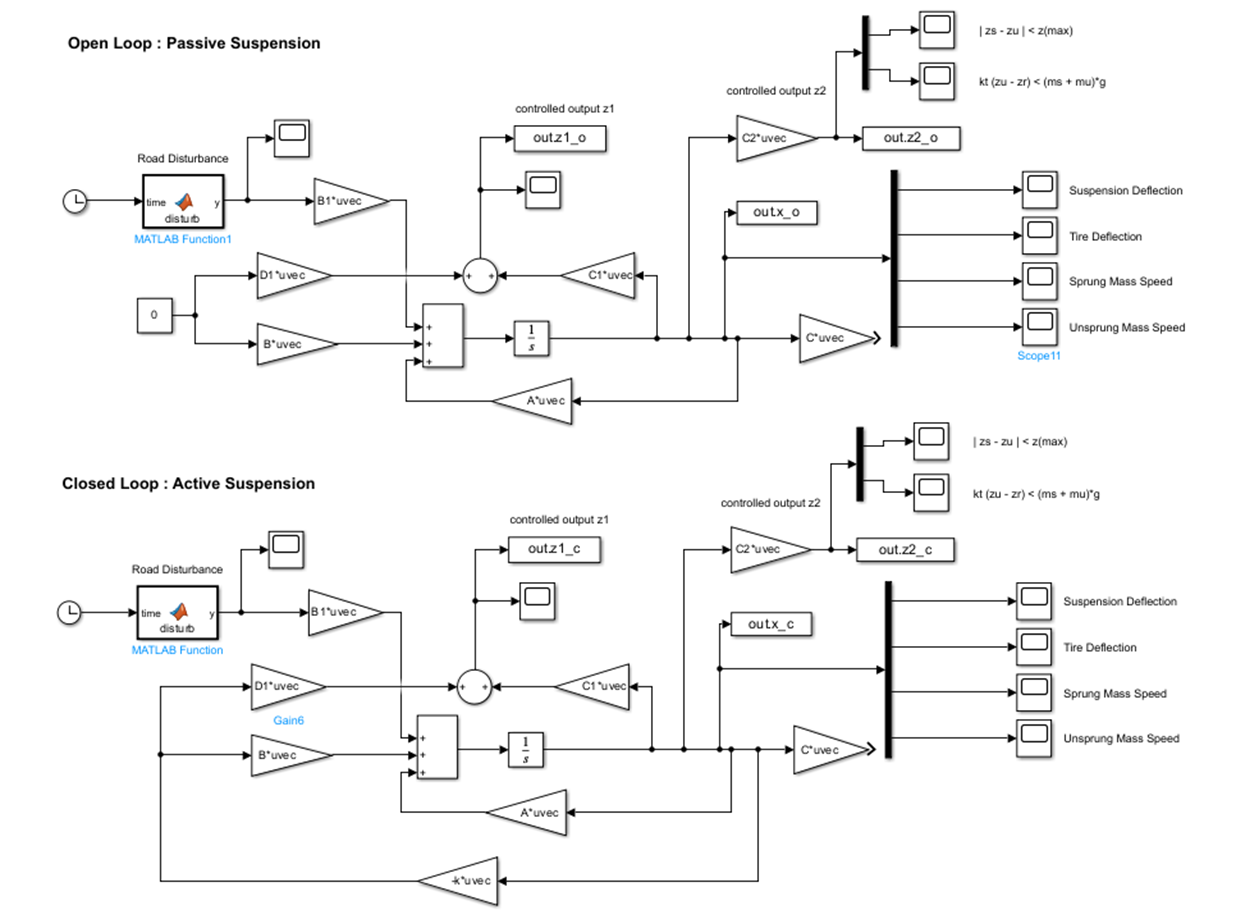
Simulink를 통해 Open loop와 Closed Loop에서의 suspension을 설계한다. 또한, Closed loop의 경우 state-estimator을 이용하여 k값을 구하고 (원하는 사양의 시스템을 만들도록 pole을 설정하는 것이 중요하다) 그에 따른 X1~X4의 결과와 Controlled Output을 비교한다.
MATLAB for Active Suspension
[1] Bump
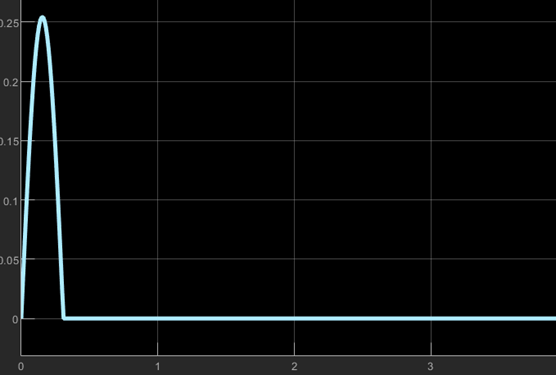

차량이 도로의 장애물 (bump)를 지날 때의 상황을 먼저 가정해보자.
이때, Bump는 1-cos(t) 함수로 모델링할 수 있고, steady-state의 w(n)에는 그 미분값인 sin(t)함수가 들어가게 된다.
< State-estimator 설계 >
p_controller=[-12.4386+31.2636i -12.4386-31.2636i -2.5762+5.7444i -2.5762-5.7444i]; % Desired poles k=acker(A,B,p_controller);
이에 대한 MATLAB 코드의 일부는 다음과 같다.
- Define the parameters
%% Define the parameters
ms = 973; % Sprung Mass [kg] (950~996kg)
mu = 114; % Unsprung Mass [kg] (110~118kg)
ks = 42720; % Suspension Spring Constant [N/m]
kt = 101115; % Tire Spring Constant [N/m]
cs = 1095; % Suspension Damping Ratio [Ns/m]
ct = 14.6; % Tire Damping Ratio [Ns/m]
zmax = 0.1; % Constraint of Suspension Deflection [m]
g = 9.81; % Gravity Acceleration [m/s^2]- Define the Matrix
%% Steady-State Model for a Quarter car
% x'= Ax + B1w + Bu
% z1 = C1x + D1u .. controlled output
% z2 = C2x .. controlled output
% y = Cx
A(1,:) = [0 0 1 -1];
A(2,:) = [0 0 0 1];
A(3,:) = [-ks/ms 0 -cs/ms cs/ms];
A(4,:) = [ks/mu -kt/mu cs/mu -(cs+ct)/mu];
B = [0; 0; 1/ms; -1/mu];
B1 = [0; -1; 0; ct/mu];
% #1 Controlled Output Matrices (z1)
C1 = [-ks/ms 0 -cs/ms cs/ms];
D1 = 1/ms;
% #2 Controlled Output Matrices (z2)
C2(1,:) = [1/zmax 0 0 0];
C2(2,:) = [0 kt/((ms+mu)*g) 0 0];
% General Observation Matrix
C = [1 1 1 0];- Use Runge-Kutta 4th method
% Function for the steady-state
X0=[0;0;0;0];
u=0;
open = @(X1,n) A*X1+B*u+B1*W(:,n);
closed = @(X2,n) (A-B*k)*X2+B1*W(:,n);
%% Runge-Kutta method for open loop
h = 0.01;
X1 = zeros(4,length(t));
X1(:,1)=X0;
for n = 1:length(t)-1
k1 = open(X1(:,n),n);
k2 = open(X1(:,n)+h*k1/2,n);
k3 = open(X1(:,n)+h*k2/2,n);
k4 = open(X1(:,n)+h*k3,n);
X1(:,n+1) = X1(:,n)+(h/6)*(k1+2*k2+2*k3+k4);
end- Get Values from Simulink
%% Plot the simulation
out = sim('suspension_simul.slx',10);
Time=out.x_c.time;
X_o=out.x_o.signals.values;
X_c=out.x_c.signals.values;
Z1_o=out.z1_o.signals.values;
Z1_c=out.z1_c.signals.values;
Z2_o=out.z2_o.signals.values;
Z2_c=out.z2_c.signals.values;이에 대한 simulation 결과는 다음과 같다.
Simulation (Plot) – Open loop and Closed loop for X1~X4
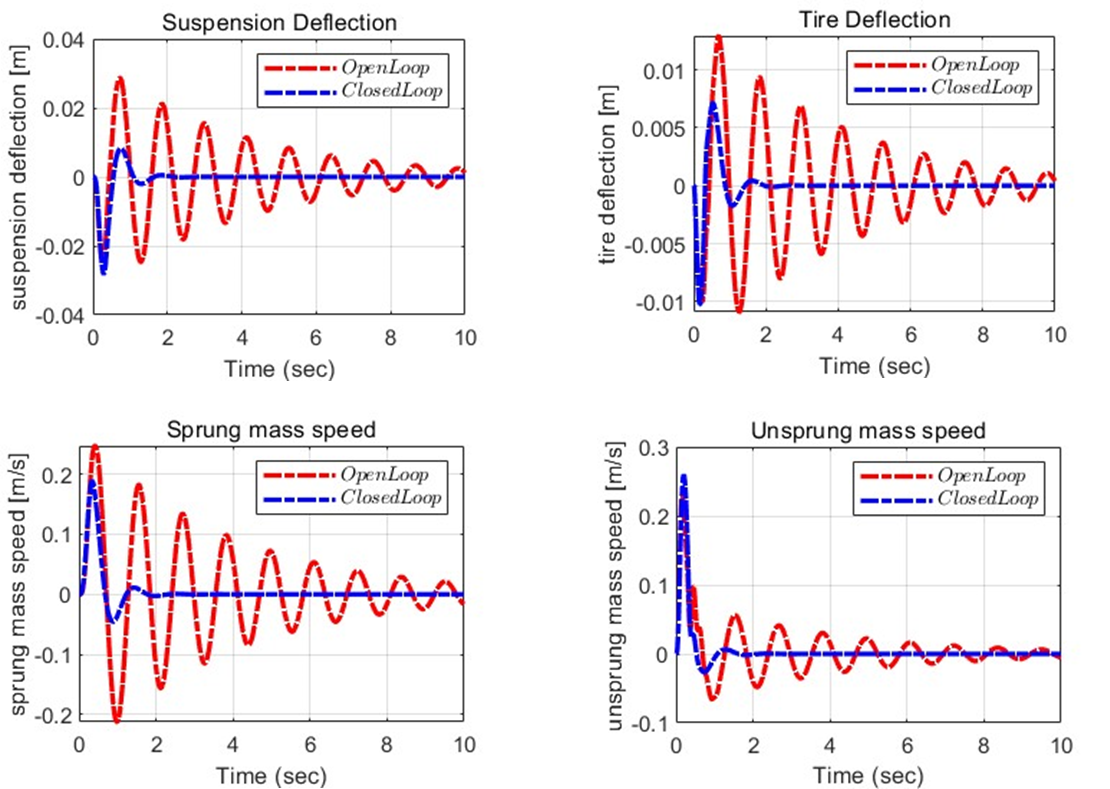
이를 보면 open loop에 비해 closed loop에서, Bump를 지나더라도 시스템이 빠르게 안정화되는 것을 관찰할 수 있다. (이는 10초동안 simulation한 결과이다)
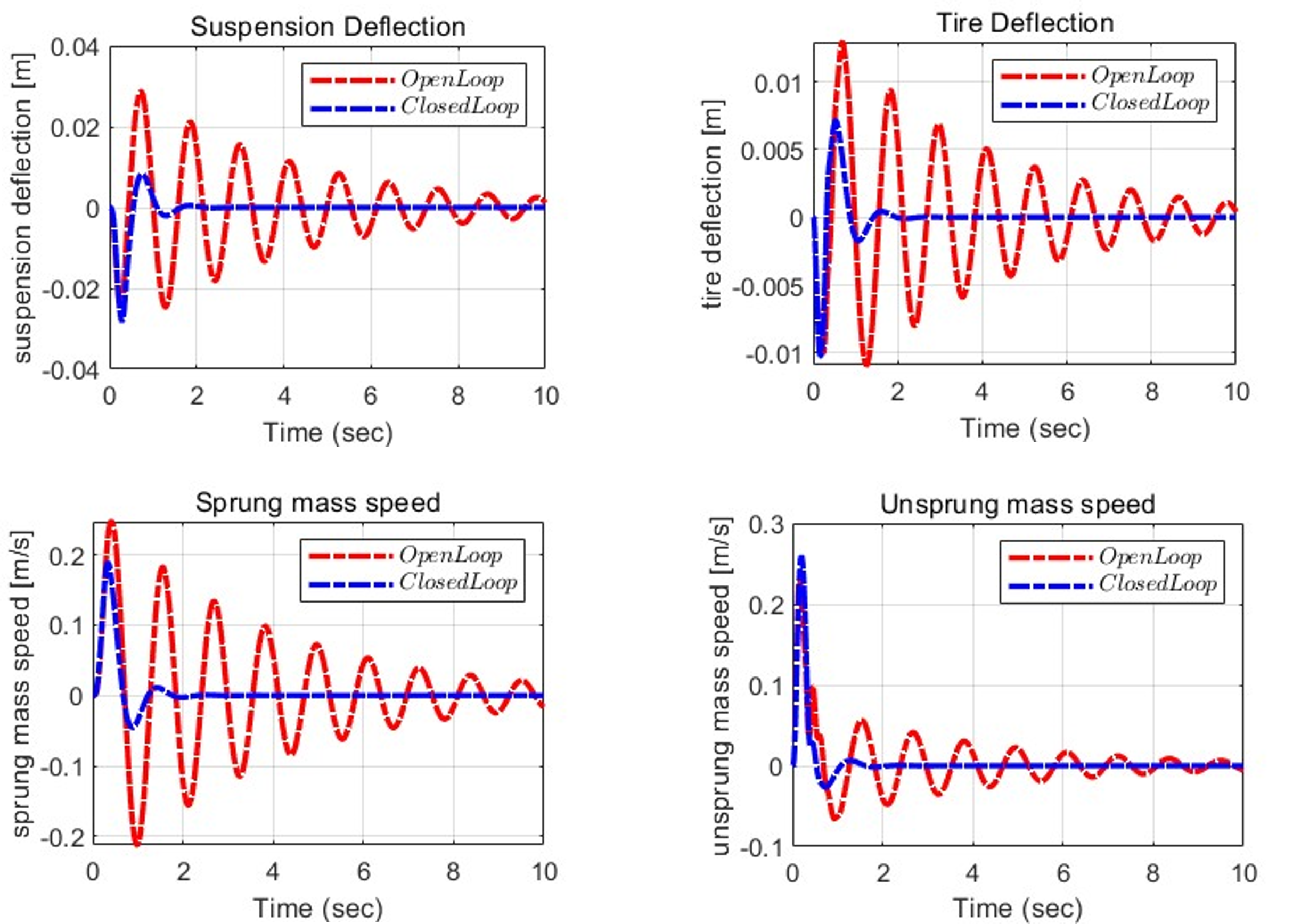
Simulation (Plot) – Open loop and Closed loop for z1 and z2

z2를 구성하는 두 가지 조건을 모두 만족하도록 결과가 도출되었음을 확인할 수 있다.
[2] Rough Road
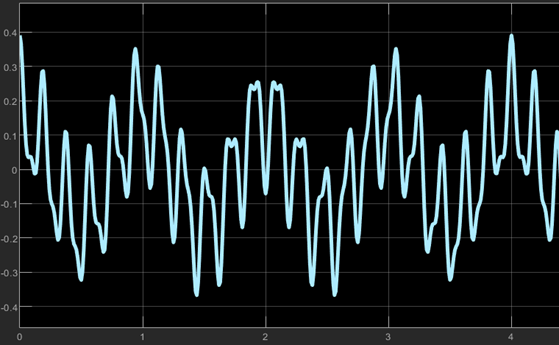
이번에는 차량이 우둘투둘한 표면의 도로를 지나는 상황을 가정해본다.
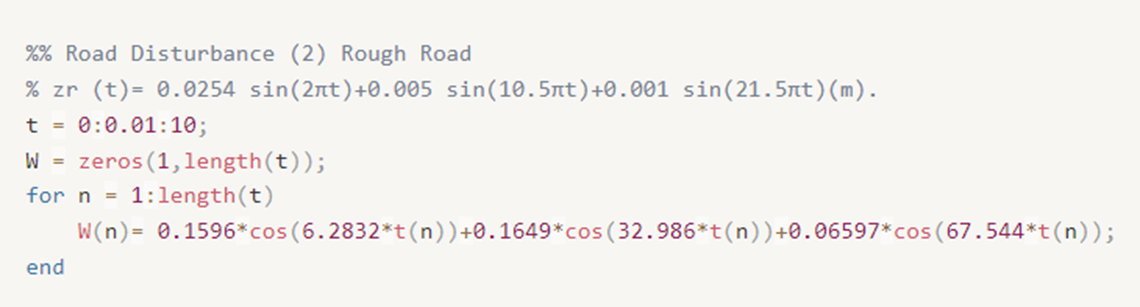
이때 Rough road 의 경우 Zr(t) = 0.0254 sin(2πt)+0.005 sin(10.5πt)+0.001 sin(21.5πt) [m] 로, 여러 sin 함수가 합성된 형태로 수학적 모델링을 할 수 있다. 또한 w(n)은 이전과 같이 미분된 형태로,
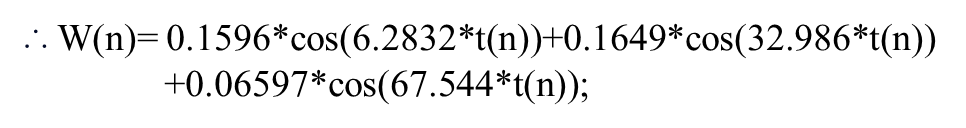
와 같이 표현될 수 있다.
위의 matlab 코드에 disturbance 정의 부분에 bump 대신 rough road에 대한 수학적 모델링을 넣으면 다음과 같은 결과를 얻을 수 있다.
Simulation (Plot) – Open loop and Closed loop for X1~X4
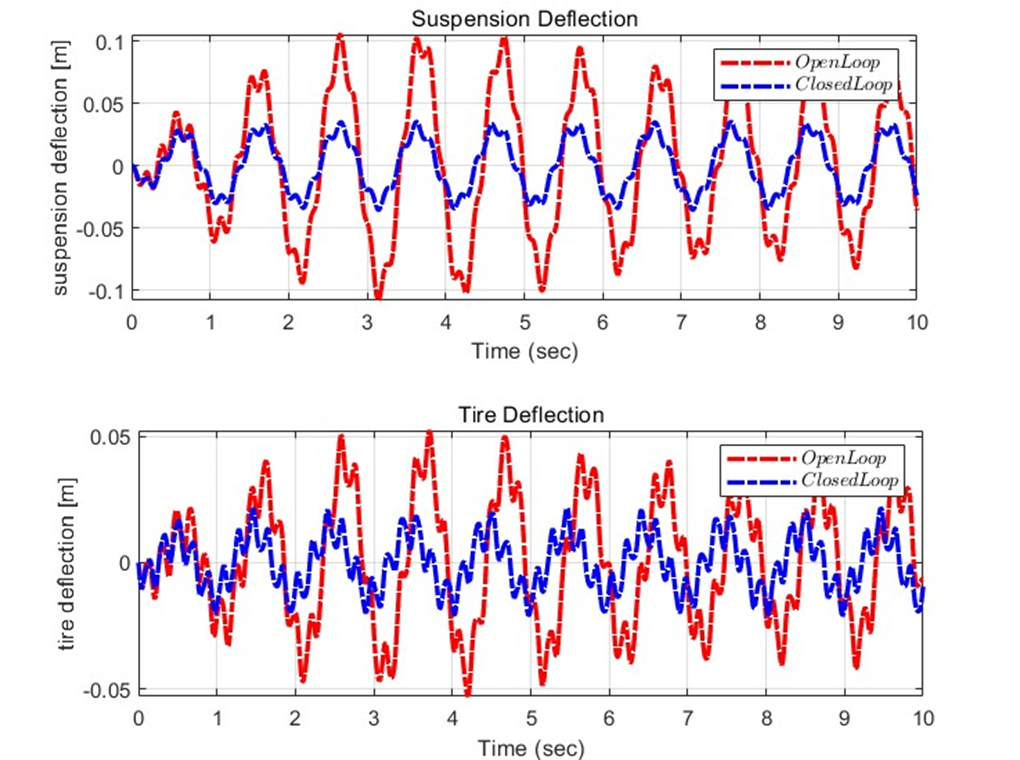
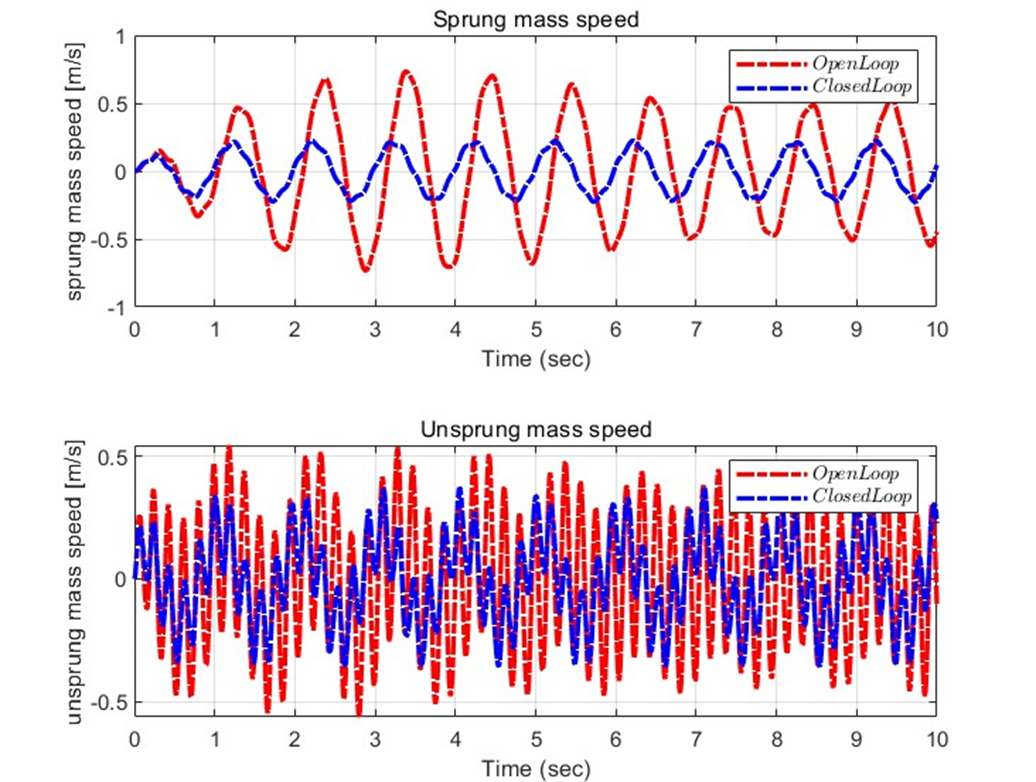
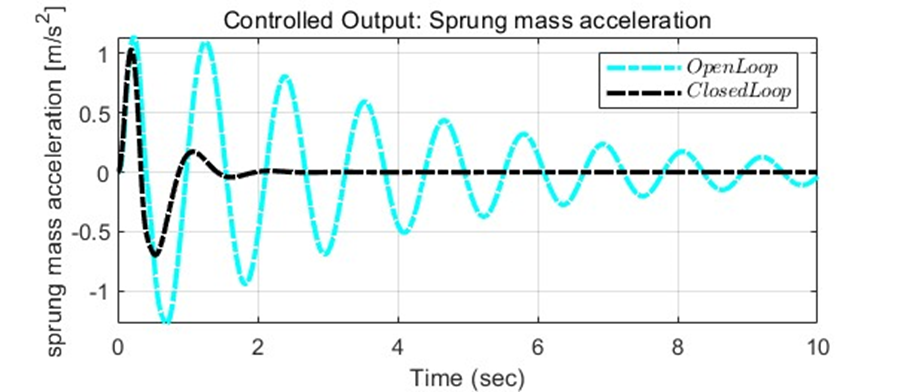
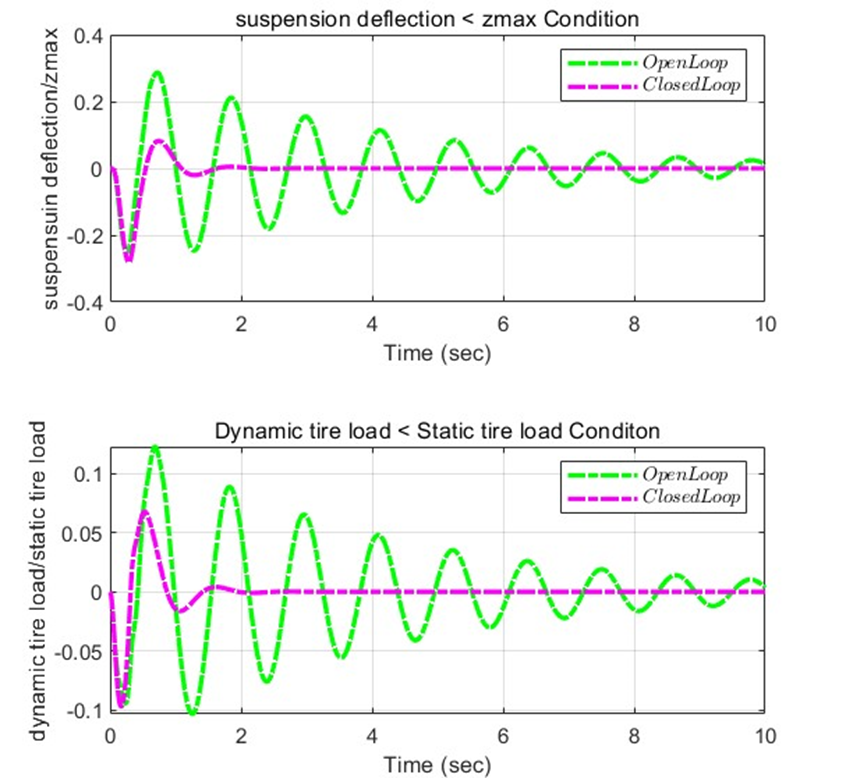
Simulation (Plot) – Open loop and Closed loop for z1 and z2
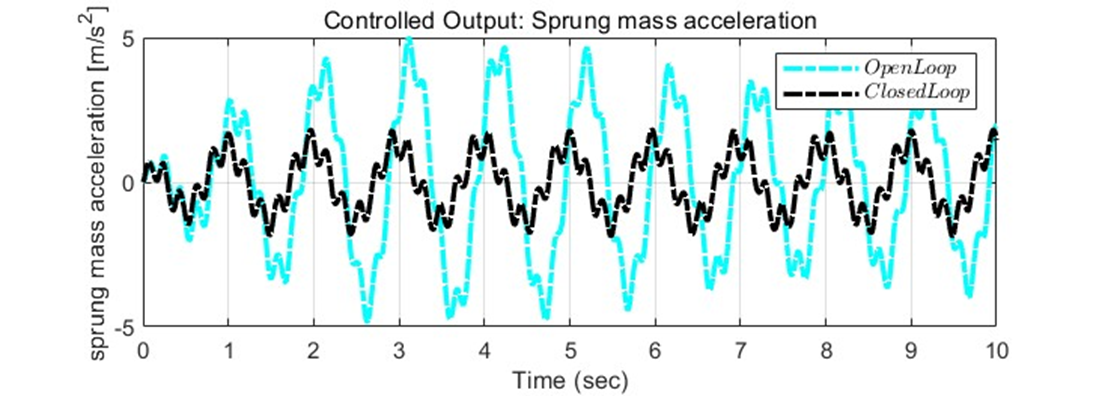
→ Closed loop with controller minimize the sprung mass acceleration, which means it improves the ride quality.
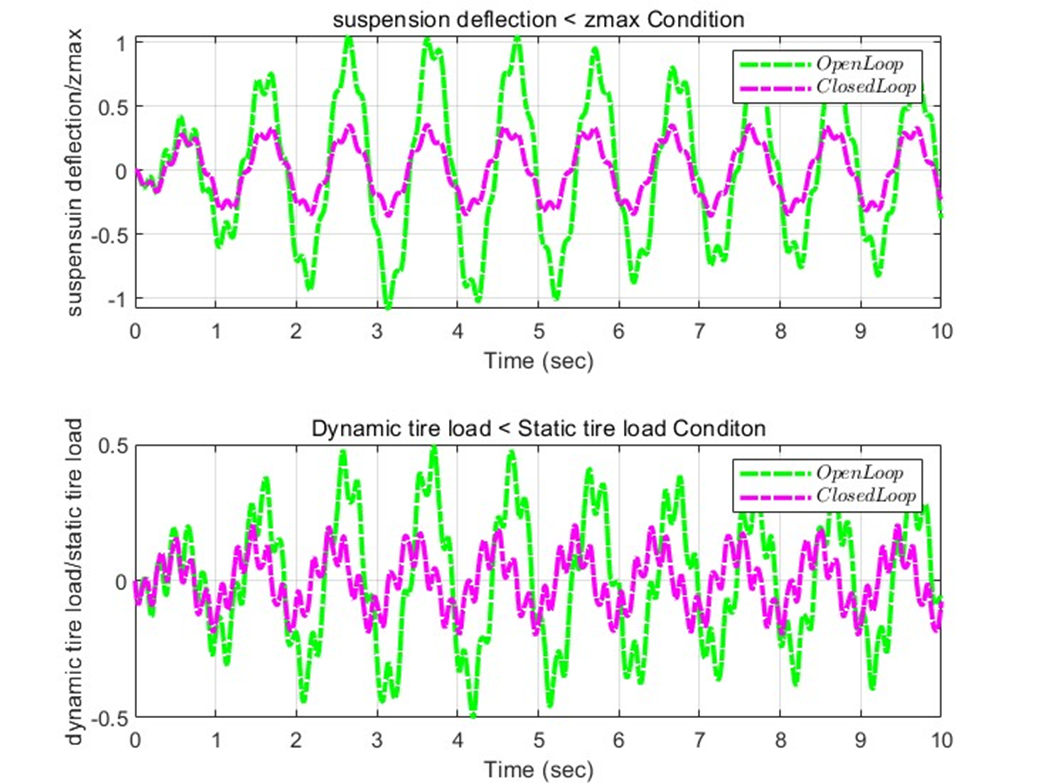
이에 따라 Closed loop의 경우, Open loop에 비해 훨씬 더 안정적으로 주행할 수 있음을 알 수 있다. Bump와 다르게, 초기 장애물 이후 초기값으로 돌아오는 형태는 아니지만, 도로 전체에 퍼져있는 장애물들에도 승차감을 향상시킬 수 있도록 안정적인 시스템을 가질 수 있었다.
[3] Random Response
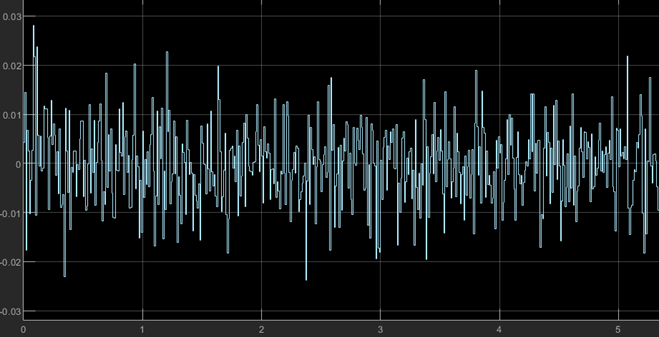

Random Response의 경우 도로의 등급을 B~E로 나누고 이에 Gaussian noise를 넣어 Random한 도로 표면 환경이 구성되도록 한다. 이때, 본 글에서는 B-Grade 도로 화경에서의 결과를 도출할 예정이다.
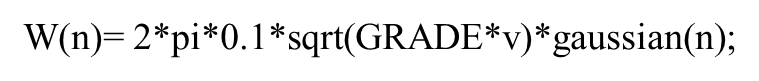
이때 위와 같은 과정을 반복하면 이에 대한 simulation 결과를 얻을 수 있다. 이 역시 유사하게 open loop보다 closed loop일 때 훨씬 더 안정적이고, 승차감이 좋은 주행능력을 가질 수 있다. 이에 대한 결과 그래프는 다음 글에서 Observer 설계와 함께 관찰하는 것으로 하자!