📌 군집 알고리즘
- 클러스터(cluster) : 군집
- 클러스터링 : 군집화. 개체 -> 군집 그룹핑
📍 k-평균 알고리즘
- k개의 중심을 무작위로 정해서 가까운 샘플들을 그룹핑
-> 그룹마다 다시 중심점을 구해서 이동, 반복
-> 한 종류만으로 이루어진 군집들이 생성
- 3차원->2차원 배열로 변경해서 수행
- n_clusters = 3 : 3개 군집으로 나눔
import numpy as np
fruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1, 100*100)
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=42)
km.fit(fruits_2d)
print(km.labels_)[2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 0 2 0 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 0 0 2 2 2 2 2 2 2 2 0 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1]
- km.labels_의 원소 종류와 각 갯수를 출력
print(np.unique(km.labels_, return_counts=True))- 구분된 클러스터 출력 함수
import matplotlib.pyplot as plt
def draw_fruits(arr, ratio=1):
n = len(arr) # n은 샘플 개수입니다
# 한 줄에 10개씩 이미지를 그립니다. 샘플 개수를 10으로 나누어 전체 행 개수를 계산합니다.
rows = int(np.ceil(n/10))
# 행이 1개 이면 열 개수는 샘플 개수입니다. 그렇지 않으면 10개입니다.
cols = n if rows < 2 else 10
fig, axs = plt.subplots(rows, cols,
figsize=(cols*ratio, rows*ratio), squeeze=False)
for i in range(rows):
for j in range(cols):
if i*10 + j < n: # n 개까지만 그립니다.
axs[i, j].imshow(arr[i*10 + j], cmap='gray_r')
axs[i, j].axis('off')
plt.show()
draw_fruits(fruits[km.labels_==0])- cluster_centers_ : 클러스터 중심
-> 다시 3차원으로 변환해서 출력
draw_fruits(km.cluster_centers_.reshape(-1,100,100), ratio=3)- transform : 샘플의 특성을 세 중심점까지의 거리로 변환
(100x100 특성을 가진 벡터 -> 3개 특성 벡터로)
print(km.transform(fruits_2d[100:101])) #100번째 샘플[[3393.8136117 8837.37750892 5267.70439881]]
-> 첫번째 클러스터에 가장 근접
- predict : 가장 가까운 클러스터로 할당
print(km.predict(fruits_2d[100:101]))
draw_fruits(fruits[100:101])[0]
- 그룹핑 완료까지 걸린 횟수
print(km.n_iter_)4
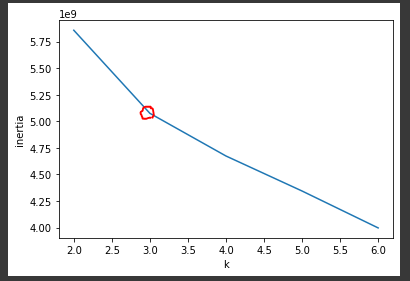
📍 최적의 k 찾기
- inertia_ : 클러스터의 중심에서 해당 클러스터에 속하는 샘플들까지의 거리 평균
-> k가 클수록 많이 나누어지므로 inertia는 감소
-> 그래프를 그렸을 때 꺾이는 지점이 최적 (엘보우메소드)
inertia = []
for k in range(2, 7):
km = KMeans(n_clusters=k, random_state=42)
km.fit(fruits_2d)
inertia.append(km.inertia_)
plt.plot(range(2, 7), inertia)
plt.xlabel('k')
plt.ylabel('inertia')
plt.show()