통계학

모수

우선 통계적 모델링 은 적절한 가정 위에서 확률분포를 추정하는 것이다.
유한한 개수의 데이터만 관찰하기 때문에 근사적으로 확률분포를 추정한다.
모수는 확률분포의 특성들이다.

모수적 방법론 : 데이터가 특정 확률분포를 따른다고 선험적으로 가정한 후, 그 분포를 결정하는 모수 추정 방법

비모수 방법론 : 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌는 방법론 ( 기계학습의 대다수 방법론이 여기에 속함 ), 모수를 쓰지 않는 것은 아니다.

확률분포 가정하는 방법

우선 히스토그램 모양 관찰

• 데이터가 2개 값만 가지는 경우 → 베르누이분포
• 데이터가 n개의 이산적인 값 → 카테고리분포
• 데이터가 [0,1]사이 값 → 베타분포
• 데이터가 0 이상의 값 → 감마, 로그정규분포 등
• 데이터가 R 전체에서 값 → 정규, 라플라스 분포 등

기계적으로 확률분포 가정해서는 안되며,

데이터를 생성하는 원리를 먼저 고려하는 것이 원칙

모수 추정

확률 분포 가정 후 모수 추정한다.

정규분포의 모수 : 평균과 분산

• 표본평균
  $\bar{X} = \frac{1}{N}\sum_{i=1}^{N}X_i$

• 표본분산
  $S^2 = \frac{1}{N-1}\sum_{i=1}^{N}(X_i-\bar{X})^2$

표집분포(sampling distribution): 통계량의 확률분포 (표본분포 sample distribution과 다르다.)

N, 즉 샘플링 개수가 커질수록 정규분포를 따른다.

원래 확률분포는 이항분포, 아무리 많이 모아도 정규분포가 되지 않는다.

그러나, 여기서 추출한 통계량의 확률분포는 많이 모으면 정규분포를 따른다.

최대가능도 추정법

Maximum likelihodd estimation (MLE)
이론적으로 가장 가능성이 높은 모수 추정방법이다.

• 데이터가 주어져 있는 상황에서 $\theta$에 따라 값이 바뀌는 함수
• 가능도를 확률로 해석하면 안되며, 가능도의 합은 1이 아니다.

데이터X가 독립적으로 추출되면 로그가능도 최적화한다.

• 로그함수 성질 → 곱을 덧셈으로 바꿔줌

위의 로그함수 성질을 이용하여 곱셈으로 정의된 확률분포 함수들을 로그 확률분포의 덧셈으로 바꾼다.

$L(\theta;X) = \prod_{i=1}^{n}P(x_i|\theta)$ ⇒ $logL(\theta;X) = \sum_{i=1}^{n}logP(x_i|\theta)$

왜 로그가능도 사용?

컴퓨터는 너무 낮은 숫자 연산 불가능하다.

그래서 곱셈으로 숫자가 너무 작아지는 것을 로그의 덧셈으로 방지할 수 있다.

추가로 경사하강법으로 가능도 최적화시 미분연산을 사용하는데

로그가능도 사용으로 선형적으로 바뀌기 때문에 $O(n^2)$에서 $O(n)$으로 줄일 수 있다.

경사하강법에서는 최소를 향해 가기 때문에 그냥 로그가능도가 아닌 negative 로그가능도를 사용한다.

딥러닝 모델 가중치 $\theta$라 표기했을 때 분류문제에서 소프트맥스 벡터는 카테고리분포의 모수를 모델링한다.

원핫벡터로 표현한 y레이블을 관찰데이터로 이용해 확률분포인 소프트맥스 벡터의 로그가능도 최적화 가능하다.

$\hat{\theta}_{MLE} = \argmax_{\theta}\frac{1}{n}\sum_{i=1}^{n}\sum_{k=1}^{K}y_{i,k}log(MLP_{\theta}(X_i)_k)$

확률분포의 거리

데이터공간의 2개의 확률분포 $P(x), Q(s)$가 있을 경우

두 확률분포 사이의 거리 계산할 때 아래 함수들 이용한다.

• 총변동 거리(TV)
• 쿨백-라이블러 발산 (KL)
• 바슈타인 거리(Wasserstein Distance)

쿨백-라이블러 발산

정의는 아래와 같다.

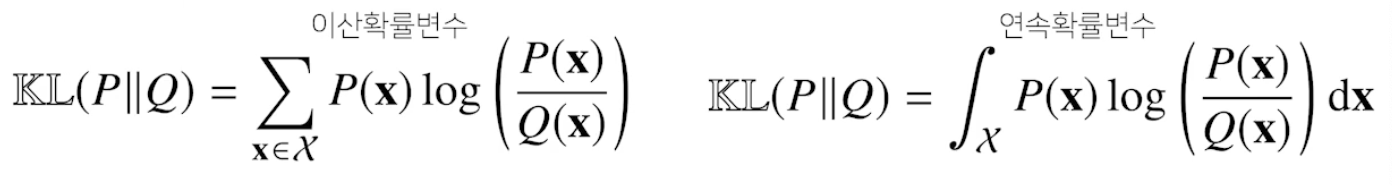
위의 식을 분해하면 아래와 같다.

위의 분해식으로 P(x)와 Q(x)와 얼마나 다른지를 구할 수 있다.

P(x)는 실제값에 대한 엔트로피이고 Q(x)는 P를 몰랐을 때 예측한 크로스 엔트로피이다.

분류 문제에서 정답P, 에측Q라고 하면 →

최대가능도 추정법에서 로그가능도(log likelihood) 최대화 는 쿨백-라이블러 발산 최소화와 같다.