🌠"데스노트" - 2281번 G4

🎃문제설명
🧛사악한 라이토는 기발한 방법을 이용하여 L(애칭 섊)을 살해한 뒤 데스노트를 다시 손에 넣었다. 라이토는 이제 이 노트에 n명의 이름을 적어 넣으려고 한다. 이때 다음과 같은 조건을 만족시키면서 이름을 적어 넣으려 한다.
우선, 이름을 적어 넣을 때 이미 정해진 순서대로 n명의 이름을 적어 넣어야 한다. 이름을 적을 때도, 노트를 위에서 아래로, 같은 줄에서는 왼쪽 맨 끝에서 오른쪽으로 차례로 적는다고 하자. 또한 이름을 적을 때 각 사람의 이름 사이에 빈 칸을 하나씩 두려고 한다. 한 줄을 적다가 그 줄의 끝에 한 사람의 이름이 다 들어가지 않고 잘리게 되면 반드시 새로운 줄에 이름을 써야 한다. 그렇지 않으면 이름이 중간에 잘려서 자칫하면 두 명의 사람이 죽게 된다. 이때, 각 줄의 끝에 사용하지 않고 남게 되는 칸의 수의 제곱의 합이 최소가 되도록 하려 한다. 이를 계산할 때 제일 마지막 줄은 앞으로 이름을 적을 기회가 있으므로 계산하지 않는다. 예를 들어 노트의 폭(너비)이 20인 다음의 경우를 보자.
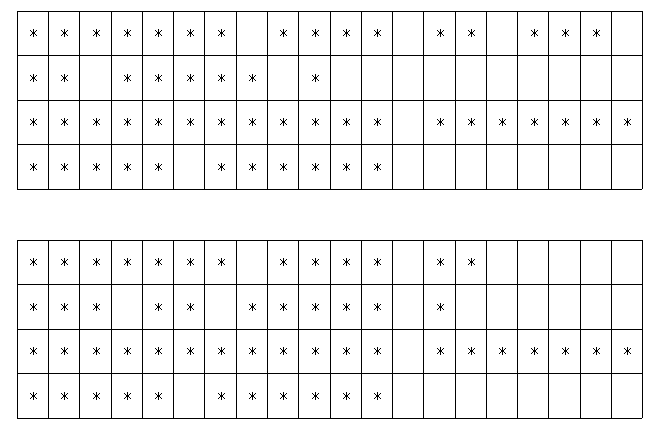
각 사람의 이름의 길이가 차례로 7, 4, 2, 3, 2, 5, 1, 12, 7, 5, 6 인 경우이다. 위와 같이 적으면 차례로 1, 10, 0칸이 남아서 제곱의 합이 101이 된다. 반면에 아래의 경우에는 5, 6, 0칸이 남아서 제곱의 합이 61이 된다.
입력
첫째 줄에 n(1 ≤ n ≤ 1,000), m(1 ≤ m ≤ 1,000)이 주어진다. m은 노트의 가로 칸의 개수(폭, 너비)이다. 다음 n개의 줄에는 각 사람의 이름의 길이가 노트에 적어야 할 순서대로 주어진다. 각 길이는 m을 넘지 않는 자연수이다.
출력
첫째 줄에 남게 되는 칸 수의 제곱의 합의 최솟값을 출력한다.
💾입출력 예
| 입력 | 출력 |
|---|---|
| 11 20 7 4 2 3 2 5 1 12 7 5 6 | 61 |
알고리즘 분류
- 다이나믹 프로그래밍
강의내용
✔️현재 이름 index에서 두가지 경우를 생각할 수 있다.
1. 다음 줄에 쓰는 경우
2. 현재 줄에 이어서 쓰는 경우
🌟문제 이해 및 풀이계획
✏️처음에는 백트래킹을 이용하여 각 이름에서 두가지 경우를 모두 해보는 코드를 작성해보았다. 하지만 이름이 1000개일 때 모든 경우는 가지가 되므로 너무 많은 수가 된다.
✏️DP를 이용하여 index와 해당 index에서 이름의 수를 기억하고, 같은 계산이 나올 때 중복 계산하지 않고 값을 가져오기만 하여 시간을 줄일 수 있다.(메모이제이션)
✍🏻내 코드1 - 오답코드
import java.util.Scanner;
public class Main {
static int n, m;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
int[] names = new int[n];
for(int i=0; i<n; i++) {
names[i] = sc.nextInt();
}
sc.close();
int idx = 1;
int cnt = names[0] + 1; // 이름 수
System.out.println(check(idx, cnt, 0, names));
}
public static int check(int idx, int cnt, int ans, int[] names) {
if(idx == n) return ans;
// 1. 다음줄에 쓰는 경우
int left = m - cnt + 1; // 남은 칸 수
int cur = check(idx+1, names[idx]+1, ans + (left * left), names);
// 2. 현재줄에 이어쓰는 경우
if(cnt + names[idx] <= m) {
cur = Math.min(check(idx+1, cnt + names[idx] + 1, ans, names), cur);
}
return cur;
}
}

❌당연히 시간초과가 난다.
⚔️DP를 이용하기 위해 grid[][] 이차원 배열을 만들어주고, grid[index][이름 수]에 결과값을 저장한다.
⚔️그리고 중복계산 방지를 위해 grid[][]의 초기 값을 모두 -1로 초기화해준 뒤, -1이면 계산하고 아니면 해당 값을 그대로 사용하도록 한다.
✍🏻내 코드2 + 강의
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static int n, m;
static int[] names;
static int[][] grid = new int[1000][1002];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
names = new int[n];
for(int i=0; i<n; i++) {
names[i] = sc.nextInt();
}
sc.close();
int idx = 1;
int cnt = names[0] + 1; // 이름 수
for(int i=0; i<grid.length; i++) {
Arrays.fill(grid[i], -1);
}
System.out.println(check(idx, cnt));
}
public static int check(int idx, int cnt) {
if(idx == n) return 0;
int ans = grid[idx][cnt];
if(ans != -1) return ans;
// 1. 다음줄에 쓰는 경우
int left = m - cnt + 1; // 남은 칸 수
ans = check(idx+1, names[idx]+1) + (left * left);
// 2. 현재줄에 이어쓰는 경우
if(cnt + names[idx] <= m) {
ans = Math.min(check(idx+1, cnt + names[idx] + 1), ans);
}
grid[idx][cnt] = ans;
return ans;
}
}
💡사실 DP에 익숙하지 않아 강의코드를 보고 왜 idx == 0일 때, return 0이될까를 계속 고민했었다. 명확한 트리구조를 사용하는 문제(예를 들면, 프로그래머스의 정수삼각형)가 아닌 문제에서 DP를 머리속에서 작성하기 힘들었는데 꼬박 하루를 생각한 것 같다... 😢
💡이차원배열을 생성하고 return값으로 계속 해당 결과값을 저장하는 방식으로 재귀 + DP를 사용할 수 있음을 배웠다. 비록 오래걸렸지만 확실하게 이해했으니 다음 문제에서는 더 빨리 풀 수 있겠지...!🙆🏻


