1. MSE(Mean-Squared Error)

우리가 처음에 AI 모델링을 한다고 하면, 가장 쉽게 접할 수 있는 손실 함수가 바로 MSE 입니다.

실제로 현재 Linear Regression 등에서는 MSE, RMSE 등을 사용하고 있습니다.

MSE는 Mean-Squared Error의 약자로써, 다음과 같은 수식을 갖습니다:

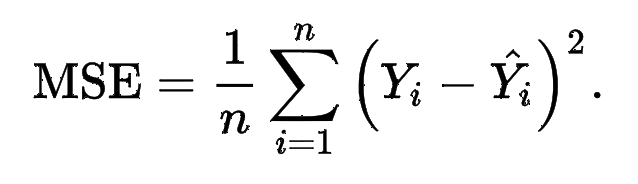
ref : https://en.wikipedia.org/wiki/Mean_squared_error

데이터의 개수가 1이라면($n=1$) 앞의 평균값 처리는 사라지고 $(Y_i - \hat{Y}_i)^2$ 만 남게 됩니다.

그래서, 만약 GAN 학습 시에 Loss value가 0.25가 나오게 된다면, $(1-0.5)^2$ 또는 $(0-0.5)^2$ 으로 가장 이상적인 수치가 됩니다. (1=True, 0=False)

이를 python 함수로 표현하면 다음과 같습니다 (데이터의 개수는 1개라고 가정합니다 → $n = 1$) → def MSE

def get_MSE(x:list, y:list):
    n = len(x)
    assert n != 0

    def MSE(x, y):
        return math.pow(float(x - y), 2)    # n = 1

    temp_list = []
    for i in range(0, n):
        temp_list.append(MSE(x[i], y[i]), 2))
    return temp_list

2. CEE(Cross-Entropy Error)

MSE에 이어서 CEE를 살펴봅시다.

CEE는 Cross-Entropy Error 의 약자입니다. CELoss 라고도 합니다.

우리는 CELoss를 살펴보기 전에, Entropy에 대해서 살펴보아야 합니다.

2-1. Entropy

엔트로피는 불확실성(Uncertainty)를 설명하는 수학적 아이디어입니다.

조금 더 자세하게 설명하자면, 확률분포가 가지는 정보의 확신도 혹은 정보량을 수치로 표현한 것입니다.

만약에, 우리가 동전을 던졌다고 했을 때, 앞면이 나올 확률이 100% 또는 뒷면이 나올 확률이 100%가 됩니다. 이런 경우에서는 불확실성=Entropy가 0이 됩니다.

무엇이 나오든지간에 우리가 100%의 확률로 예측이 가능한 것이기 때문입니다.

수식은 다음과 같습니다.

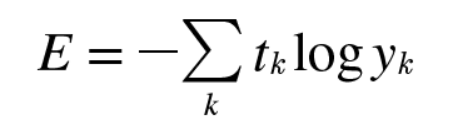
엔트로피는 모든 가능한 결과의 합입니다.

위 CE Loss 의 경우는 multi-class의 경우에서 사용 가능합니다. 우리가 앞에서 Entropy에 대해 살펴본 것 처럼 위는 확률 값을 필요로 합니다.

그래서 NN의 마지막 layer에 Softmax를 쓰는 이유입니다. 아래 수식(Softmax, $\sigma$)은 간략하게 설명하자면, 현재 값을 입력 값의 총 합으로 나눈 것입니다.

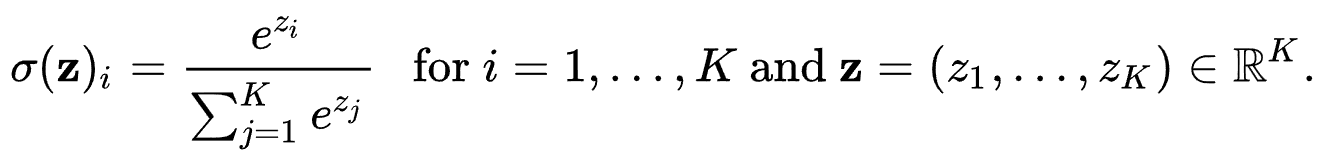
Softmax Function. ref : https://en.wikipedia.org/wiki/Softmax_function

만약에, True/False 를 구분하는 single-class의 경우에서는 BCELoss를 사용합니다. (Binary Cross-Entropy Loss)

BCELoss 의 식은 다음과 같습니다:

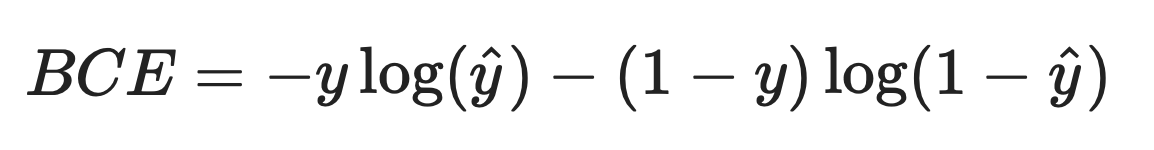
이를 파이썬 코드로 표현하면 다음과 같습니다. (데이터의 개수는 1개라고 가정합니다 → $n = 1$) → def MSE

def get_CEE(x:list, y:list):
    n = len(x)
    assert n != 0

    def CEE(x, y):
        return (-1 * y * math.log(x)) + (-1 * (1 - y) * math.log(1 - x))
        
    temp_list = []
    for i in range(0, n):
        temp_list.append(CEE(x[i], y[i]))
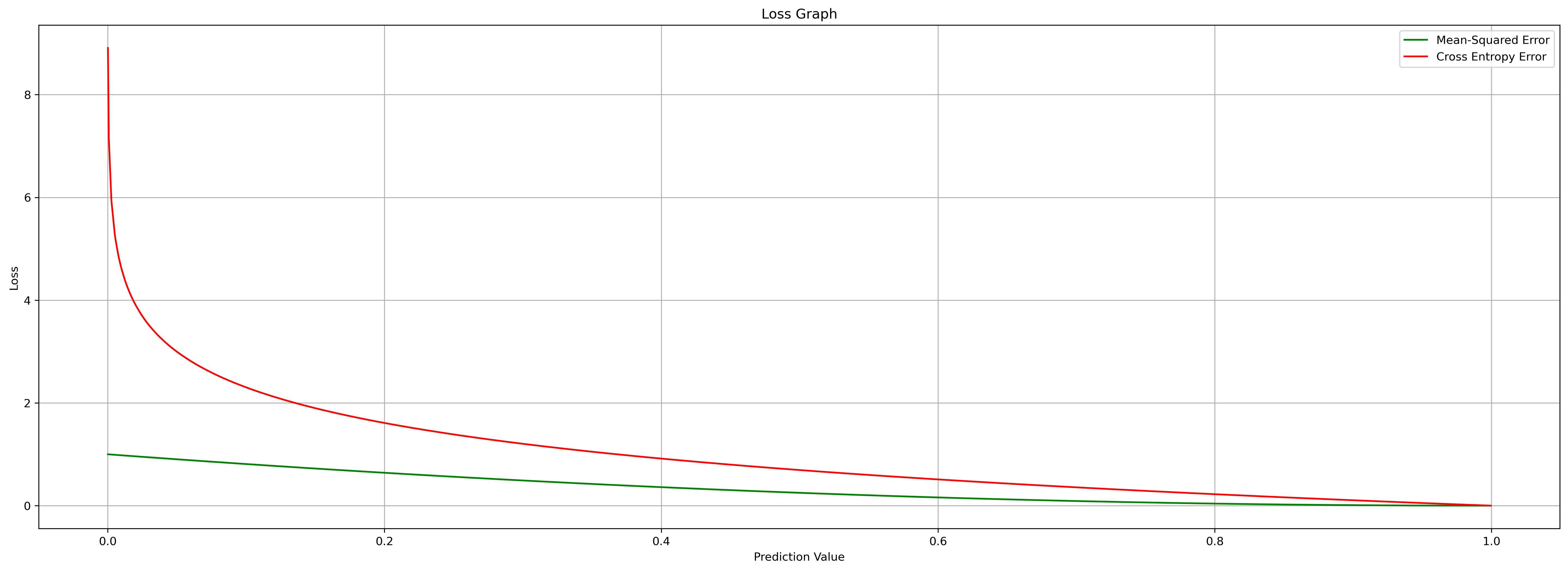
    return temp_list

이제, 위에서 살펴본 MSE와 Binary CEE를 사용하면 손실값에 대한 그래프를 그려볼 수 있습니다.

import math
from matplotlib import pyplot as plt
import numpy as np

def get_MSE(x:list, y:list):
    n = len(x)
    assert n != 0

    def MSE(x, y):
        return math.pow(float(x - y), 2)    # n = 1

    temp_list = []
    for i in range(0, n):
        temp_list.append(MSE(x[i], y[i]), 2))
    return temp_list

def get_CEE(x:list, y:list):
    n = len(x)
    assert n != 0

    temp_list = []
    for i in range(0, n):
        temp_list.append((-1 * (y[i]) * math.log(x[i])) + (-1 * (1 - y[i]) * math.log(1 - x[i])))
    return temp_list

if __name__ == "__main__":
    x_list = sorted([np.random.random() for x in range(0, 1000)])
    y_list = [1.0 for x in range(0, 1000)]

    mse_ret = get_MSE(x_list, y_list)
    cee_ret = get_CEE(x_list, y_list)

    plt.figure(dpi=300, figsize=(24, 8))
    plt.title("Loss Graph")
    plt.plot(x_list, mse_ret, label='Mean-Squared Error', color='green')
    plt.plot(x_list, cee_ret, label='Cross Entropy Error', color='red')
    plt.xlabel("Prediction Value")
    plt.ylabel("Loss")
    plt.legend()
    plt.grid()
    plt.savefig(f"losses.png", format="png", bbox_inches="tight")
    plt.show()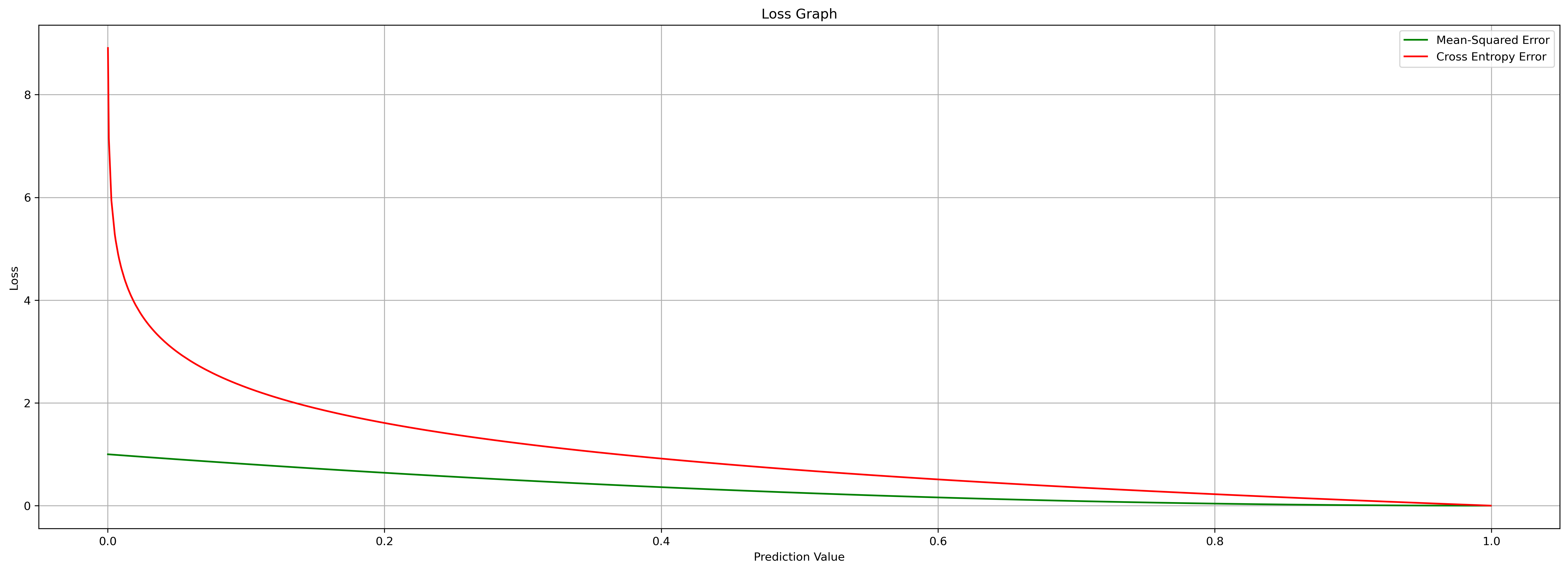

우리는 위 그래프를 통해, “MSE는 선형적으로 손실값에 대해 감소하는 1차함수의 그래프이고, Binary CEE는 손실값이 크면 클수록 더 높은 값을 보임”을 알 수 있습니다.

우리가 딥러닝 학습을 할 때, Cross Entropy 함수를 쓰는 이유는, 위처럼 일반적인 경우에서, 손실 값이 클 때 더 큰 값을 갱신하기 때문입니다.

2-2. GAN에서 이상적인 손실 값

우리가 이전에 GAN 학습 시에, 0.69라는 값이 가장 이상적인 손실 값이라고 했었습니다.

그 이유는 다음과 같습니다.

• GAN 학습은 이진 CELoss 를 통해 값을 갱신합니다.
• 그 값은 True일 때 1.0, False일 때 0.0 입니다.
• 1.0과 0.0에서 가장 불안정한 척도는 0.5입니다.
• $x=0.5, y=1.0$ 일 때의 교차 엔트로피는 $-1.0 \times ln(0.5) - (0.0 \times ln(1 - 0.5)) = 0.693$

이로 인해, GAN 학습 시에 Discriminator와 Generator의 균형이 맞다면 0.693 이라는 손실 값이 가장 이상적인 수치입니다.

3. MLE(Maximum Likelihood Estimation)

MLE 는 Maximum Likelihood Estimation의 약자로, 이를 한글로 번역하면 ‘최대 “우도” 측정법’ 으로 말할 수 있습니다.

우리가 GAN에서 늘 얘기하는 데이터셋의 분포(= 이 데이터가 나왔을 확률 분포)와 관련이 있습니다.

3-0. 기본

예를 들어서, “구름이 흐릴 때 비가 올 확률이 얼마나 될까?” 라는 가정이 있습니다.

여기서 구름이 흐릴 때 를 확률 변수 $x$ 라고 하고, 비가 올 확률은 이 $x$ 에 대응하는 $y$ 값이 될 것입니다.

확률 변수 $x$는 2종류가 있습니다:

• 이산 확률 변수 : 주사위 눈 처럼 연속하지 않은, 이산 상태의(discrete) 값들입니다.
• 연속 확률 변수 : 셀 수 없는(uncountable) 값으로, 어떠한 상태가 아닌 영역으로 표시할 수 있는 값입니다.

3-1. 확률 분포

확률 분포는 영어로 Probability Distribution 입니다.

이는 미지수 $x$ 에 대응하는 $y$ 의 분포입니다. 우리가 normal distribution(=Gaussian distribution, 연속확률분포 중 1개), 즉 정규 분포를 표현하기 위해서 평균(mu, $\mu$), 표준편차(sigma, $\sigma$) 를 제공하고 $x$ 값을 넣게 되면 어느 $y$ 값이 나오는지 알 수 있습니다.

즉, 다시 말해서, 평균과 표준편차에 따라서 달라지는 Probability Distribution이기 때문에 $x$ 값에 따라 결과값 $y$ 가 결정되는 것입니다.

💡 참고 : $\mu=0$, $\sigma=1$ 일 때를 Standard Normal Distribution, 표준 정규 분포 라고 합니다.

평균, 표준편차에 따라 서로 다른 Normal Distribution의 그래프.

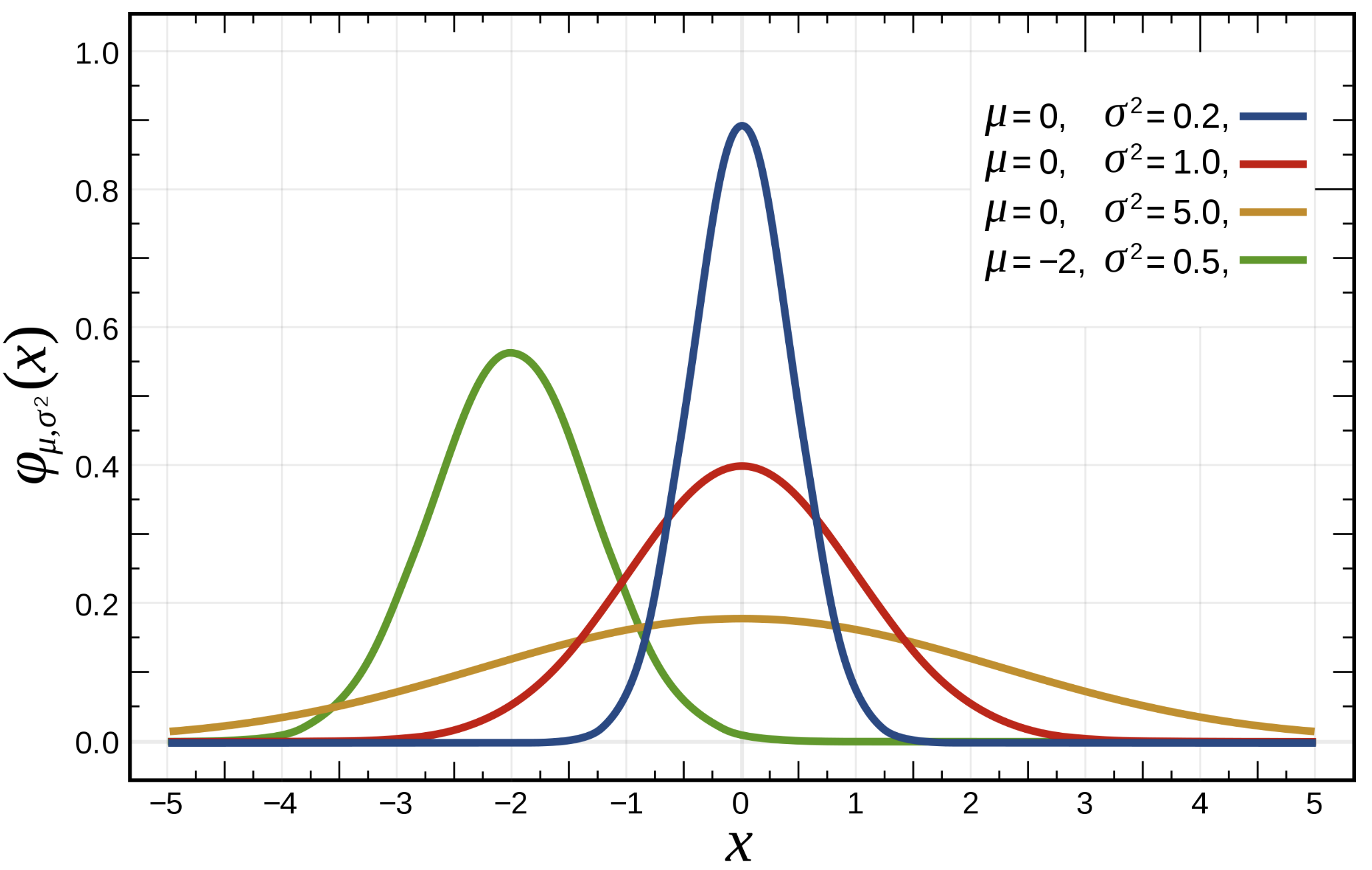
여기서 $\mu$, $\sigma$ 를 모수, 즉 아래에서 얘기할 $\theta$ 라고 볼 수 있습니다.

모수란 모집단의 parameter, 이는 모평균과 모분산(분산 = 표준편차 $\sigma$의 제곱의 합)으로 이루어져 있습니다.

참고 : 분산에 제곱근을 씌우면 표준편차가 됩니다.
표준편차는 평균으로부터 원래 데이터에 대한 오차 범위의 근사값입니다.

이를 수식으로 표현하면 다음과 같습니다 → $**f(x;\theta) = f(x;\mu, \sigma^2) = N \sim X(\mu, \sigma^2)$**

또한, 정규분포의 식은 다음과 같습니다.

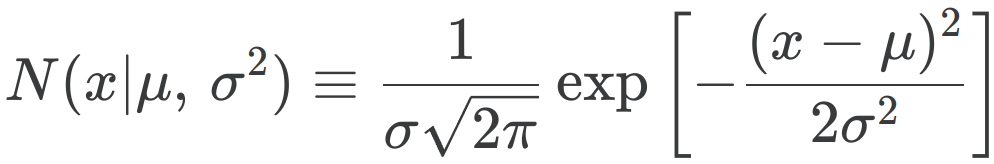
3-2. MLE

하지만 MLE는 반대입니다. MLE는 추정문제로써, 이미 $x$ 값들은 주어지고 모수(theta = $\theta$)는 모르는 상태입니다.

추정문제이기 때문에 MLE 에서는 이 $\theta$를 추정하는 것을 목표로 합니다.

우리가 위에서 모수에 대해서 언급을 했는데, 통계학에서 말하는 조사는 2가지 방식이 있습니다.

• 전수 조사
• 표본 조사

전수 조사란, 말 그대로 모든 수에 대해서 조사하는 방식입니다.

우리가 예를 들어 설문조사를 한다고 하면, 전 국민에게 모든 응답을 들어서 통계적으로 나타내는 것이 전수 조사입니다.

하지만 통계학은 이렇게 전수 조사를 하지 않더라도 predict 하여 대략적인 근사 결과를 알 수 있는데, 이를 표본을 추출하여(sampling) 조사하는 표본 조사입니다.

표본을 조사함으로써, 모집단의 특성(평균과 표준편차)을 파악하는 것을 “Estimation”, 추정이라고 합니다.

최대 우도(= 최대 가능도, Maximum Likelihood)를 추정하려면 질문이 조금 바뀌게 됩니다.

원래 “구름이 흐릴 때 비가 올 확률이 얼마나 될까?” 가 질문이었다면, 추정 문제에서는 “만약 비가 온다면, 구름의 상태는 얼마나 흐린 상태일까?” 가 됩니다.

다시 말해서, 어떠한 상태가 주어지고 그 상태가 어느 확률 분포에 포함될 가능성이 가장 높은지 추정하는 것 이 “최대 우도 추정” 입니다.

이게 GAN framework와 어떤 관련이 있느냐? 라고 한다면, 이제 생각해 볼 수 있습니다.

• Discriminator는 입력 이미지가 정답 데이터셋의 분포에 포함되는 지 판별하는 판별자입니다.
• Generator는 Discriminator를 속여야 합니다.

다시 말해서, Generator로 생성된 이미지는 Disriminator가 그 이미지를 보고 “아, MLE로 생각해 보았을 때, 정답 데이터셋의 분포에 있을 가능도가 가장 높아 → True Dataset이야!” 라고 속일 수 있어야 합니다.

그러면 이번에는, Discriminator는 그 서로 다른 확률 분포를 어떻게 알 수 있을까요? 여기서 사용되는 것이 KL-Divergence (쿨백-라이블러 발산) 입니다.

KL-Divergence 에 대해서는 다음에 알아보도록 하겠습니다.