-
회귀
데이터의 값이 평균과 같은 일정한 값으로 돌아가려는 경향
(아무리 키가 큰 집안의 아이도 무한정 키가 커지지는 x)회귀: 여러개의 독립변수와 종속변수 간의 상관관계를 모델링하는 기법을 통칭
머신러닝에서 회귀의 핵심:
최적의 회귀 계수를 찾아내는 것! (W1, W2, ..)선형회귀 vs 비선형회귀: 회귀계수의 제곱여부! (독립변수 x**2는 상관없음!)
-
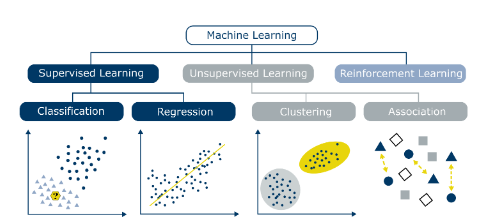
분류 vs 회귀
분류: 결과 값이 category값(이산적인 값으로)회귀: 숫자값(연속값)
https://miro.medium.com/max/1400/1*kcBsTJsIiDEC9XcizmnmYg.png
[지도학습]
정답이 있는 데이터를 활용해 데이터를 학습시키는 것
대표적으로 분류(결과가 카테고리로 나뉠 때), 회귀(결과값이 실수)
[비지도학습]
정답 라벨이 없는 데이터를 비슷한 특징끼리 군집화하여 새로운 데이터에 대한 결과를 예측하는 법
대표적으로 클러스터링, K Means
[강화학습]
자신이 한 행동에 대한 보상(reward)를 받으며 높은 점수를 얻는 방법을 찾아가는 것
특정 학습 횟수 이후에, 높은 점수(reward)를 획득할 수 있는 전략이 형성됨
(행동을 위한 행동 목록은 사전에 정의 되어 있음)
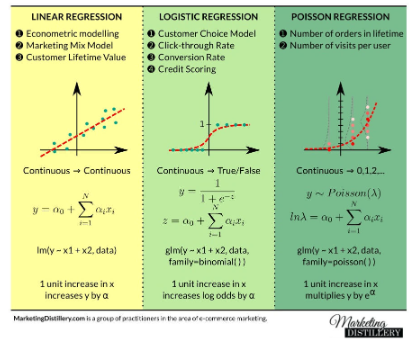
- 선형 회귀의 종류
일반선형회귀
릿지, 라쏘, 엘라스틱넷
로지스틱회귀(사실은 분류에 사용되는 선형 모델)
-
단순 선형 회귀(SR): 피처가 1개
y = w0 + w1*x -
RSS 기반의 회귀 오류 측정
RSS: 회귀의 비용함수(오류값의 제곱의 합)단순선형회귀에서, RSS식에는 w0과 w1만 남는다.
회귀 알고리즘에서는 RSS(비용함수)를 최소로 만들어야 한다
-
비용 최소화하기: 경사하강법(Gradient Descent)
점진적으로 반복적인 계산을 통해 w를 업데이트 시키기 -
R(w)의 편미분
-
사이킷런 LinearRegression 클래스
-
선형회귀의 다중 공선성 문제
피처간의 상관관계가 높으면, 분산이 커져서, 오류에 매우 민감해진다
상관관계가 높은 피처들 중에 중요한 피처만 남겨야 한다! -
회귀 평가 지표
MSE: mean squared error
MSLE: MSE에 로그를 적용한 것 -
Scoring 함수에 회귀 평가 적용 시 유의사항
-
다항회귀
독립변수(x)의 식이 단항식이 아닌 2차, 3차 방적식과 같은 다항식으로 표현되는 것 -
PolynomialFeatures
다항식을 하나의 단항식으로 바꾼 다음에 LinearRegression학습을 시킨다
ex) x1**3 = z1 으로 변환
-
규제선형회귀
다항회귀에서 회귀계수가 기하급수적으로 커지는 것을 제어해야한다최적모델을 위한 cost함수 구성요소
= 학습데이터 잔차 오류 최소화 + 회귀계수 크기 제어규제: aplpha값으로 페널티를 부여해, 회귀 계수 값의 크기를 감소시킴
릿지회귀: w의 제곱에 대해 패널티 부여
라쏘회귀: W의 절댓값에 대해 패널티 부여 -
릿지 회귀
회귀계수의 크기를 주기적으로 감소시킴 -
라쏘회귀
불필요한 회귀 계수를 급격하게 감소시켜 0으로 만들고 제거 -
엘라스틱넷 회귀: L2+L1
alpha: = L1의 alpha + L2의 aplha
-
선형회귀모델을 위한 데이터 변환
타깃값변환: 타깃값을 반드시 정규 분포로 만들어야 함(주로 로그 변환 적용)
피처값 변환:
StandardScaler
MinMaxScaler데이터 인코딩은 원-핫 인코딩 적용
-
피처 데이터 변환에 따른 예측 성능 비교
원본 vs 표준정규분호 vs 표준정규분포+2차다항식 vs 최소최대정규화 vs 로그변환
-
로지스틱 회귀
시그모이드 함수 최적선을 찾고, 이 시그모이드 함수의 반환 값을 확률로 간주해 확률에 따른 분류를 결정한다주로 이진 분류에 사용됨.
예측확률은 시그모이드 함수의 출력값
예측확률이 0.5이상이면 예측값을 1로.
-
회귀트리
CART: Classification and regression trees- RSS를 최소화하는 규칙 기준에 따라 분할
- 최종 분할된 영역에 있는 데이터들의 평균값들로 학습/예측
-
회귀트리의 오버비팅
트리크기, 노드 개수 제한 등의 방법 통해 오버피팅 개선.
ref: "파이썬 머신러닝 완벽가이드", 권철민, 위키북스
