Identity Mappings in Deep Residual Networks(Pre-activation ResNet)

논문 제목 : Identity Mappings in Deep Residual Networks
논문 링크 : https://arxiv.org/pdf/1603.05027.pdf

이번 논문은 Pre-activation ResNet이다.
지난 논문(WRNs)을 읽으며 Pre-activation을 무진장 많이 언급하길래,
대체 뭘 했길래 이 논문에서는 저녀석의 성능을 뛰어넘을려고 애를 쓸까 하는 생각이 들었다.
논문 공부법 - "참고 문헌을 따라간다"에 입각하여 이 논문도 읽게 되었다.

후기 :
중간 실험에서 conv3x3->conv3x3 2개 로 좁혀나가는 과정이 마음에 들었다.
Gating은 죄다 실패한게 좀 웃프긴 했다.
Pre-activation이 성공한 이유가 직관적으로 이해가 되니 되게 신기했다.
아.. 이래서 되는구나~
학습 한 번에 몇 시간 ~ 몇 주가 걸리니 이 무수한 실패를 넘어 full pre-activation 만들때까지 얼마나 오랜 시간이 걸렸을까 싶다.. 대단하다.
Appendix에 학습 detail이 있다. 굳이 쓰기 싫어서 안 옮겨 적었다.
코드는 그냥 기본 ResNet에 BN, activation만 넣어주면 되니 따로 쓰지 않겠다.

Abstract

이 논문에서는 residual building block의 propagation formula를 더 살펴볼 예정이다.
Identity mapping의 중요성에 대해 연구하고,
이를 통해 더 빠르게 학습하고 일반화 능력이 좋은 새로운 residual unit을 만들었다.

1. Introduction

Residual unit은 다음과 같은 형태를 지니고 있다.

여기서 기존의 ResNet의 경우 $h(x_l)=x_l$은 identity mapping, f는 ReLu 이다.

논문에서는 residual unit 내부 뿐만 아니라 network 전체에서 "direct" path를 만들고자 했다.
또한 $h(x_l)$과 $f(y_l)$이 모두 identity mapping이라면, signal이 forward, backward 모두에서 direct하게 propagate될 것이다.

이 두 조건(bold체)을 만족시키면 학습시키기가 더욱 쉬워진다.

Skip connection의 역할을 이해하기 위해 $h(x_l)$을 다양하게 바꾸며 실험한 결과,
$h(x_l)=x_l$인 identity mapping이 가장 빠른 error reduction과 가장 낮은 training loss를 보여줬다.
반면 scaling, gating, conv1x1 등을 통과한 경우 더 높은 training loss와 error가 나타났다.
이는 "clean" information path가 최적화에 도움됨을 보여준다.

$f(y_l)=y_l$을 만들기 위해, activation function(ReLU, BN)을 weight layer의 "pre-activation"으로 생각했다.
이를 사용해 unit design을 했고(Fig. 1(b)), 그 결과 CIFAR, ImageNet에서 좋은 결과를 얻을 수 있었다.

2. Analysis of Deep Residual Networks

ResNet은 "Residual Units"을 쌓아 만든 모듈화된 구조이다.
Residual unit을 살펴보자.

• $x_l$은 l번째 residual unit의 input이다.
• $\mathcal{W}_l$은 weight set이다.
• $\mathcal{F}$는 residual function이다.
  Residual function이란, $y_l - h(x_l)$을 의미한다(output에서 identity mapping을 뺀 나머지, ResNet 논문 참조)
• f는 element-wise addition(원소별 합) 후 operation이다(ResNet에서는 ReLU).
• h는 identity mapping이다.

Forward

만약 f 역시 identity mapping이라 가정한다면(즉, $x_{l+1}=y_l$),
그렇다면 위의 식은 다음과 같이 쓸 수 있다.

이를 계속 더하면 다음과 같다.

이 식은 어떠한 deeper unit L과 shallower unit L에 대해서도 성립한다(더하면 l=0도 만들 수 있다).

즉, $x_L$은 어떤 shallower unit $x_l$과 residual function($\sum$ 형태)의 합으로 표현할 수 있다.
이는 기존의 "plain network"의 $x_L$이 matrix-vector product라는 것과 대조된다.

Backward

또한 backward propagation도 마찬가지이다.
Loss function $\varepsilon$에 대해서 chain rule을 적용해보자.

여기서 보면, loss $\varepsilon$에 대한 shallow(back propagation에서는 deep layer가 먼저 쓰임) $x_l$의 gradient는 두개로 쪼개진다.
1) $\frac{\partial \varepsilon}{\partial x_L}$, 이는 weight layer 없이 deep layer L에서 shallow layer l로 직접 전해진다.
2) $\frac{\partial}{\partial x_L}(\frac{\partial}{\partial x_l}\sum_{i=l}^{L-1}\mathcal{F})$는 weight layer를 통과한 값이다.

$\frac{\partial \varepsilon}{\partial x_L}$이 information을 direct back propagate한다.

또한, $\frac{\partial \varepsilon}{\partial x_l}$(shallow gradient 값)는 mini batch로 사라지지도 않는다.
그 이유는 $1+\frac{\partial}{\partial x_l}\sum_{i=l}^{L-1}\mathcal{F}(x_i, \mathcal{W}_i)$가 0이 되려면 $\frac{\partial}{\partial x_l}\sum_{i=l}^{L-1}\mathcal{F}$가 mini batch의 모든 sample에 대해 -1이어야 하는데,
우연으로 -1이 될 순 있어도 항상 그럴수는 없다.
따라서 gradient vanish를 막아준다.

(갑자기 근데 한 번이라도 -1이 되어 사라지면 끝 아잉교 싶었는데 아니었다.
그 이유는 우연히 -1이 되어 $x_l$ gradient가 0으로 사라졌다 치자.
근데 그게 다른 l에 대해서도 모두 그런가? 아니다.
l이 l+1처럼 바뀌는 순간, -1에서 다른 값으로 바뀌어 그 gradient는 0이 아니다.
즉, 이전 layer, 이후 layer의 gradient에 딱히 의존적이지 않다!
기존의 CNN들은 이전에 0이면 계속 0이었지만, 이건 더해주는 형태라.. 그렇지 않다.)

Discussions

즉 signal이 forward, backward 모두에서 directly propagate될 수 있음을 시사한다.
이는 2개의 identity mapping 덕분이다(h, f).

Fig. 1, 2, 4의 grey arrow는 이러한 direct propagate(아무 연산도 추가되지 않으면 "clean")를 보여준다.

3. On the Importance of Identity Skip Connections

Identity shortcut에 scalar 값을 곱해 수식을 변경했다.
Forward

여기서 $\hat{\mathcal{F}}$를 기존의 $\mathcal{F}$에 $\Pi _{j=i+1}^{L-1}$를 합친 것이라 정의하자.
Backward

Backward의 수식을 보면, $\lambda_l>1$이면 값이 exponentially하게 커질 것이고,
$\lambda<1$이면 small and vanish할 것이다.
즉, 최적화에 어려움이 있다.

또 만일 $\lambda_l$이 gating and conv1x1이었다면,
$h(x_l)=\lambda_lx_l$일때 Backpropagation의 $\Pi _{i=l}^{L-1}\lambda _i$(scalar)가 $\Pi_{i=l}^{L-1}\hat{h}$(vector)가 되어 정보 전달을 지연시키고 학습을 방해한다.

3.1 Experiments on Skip Connections

실험은 CIFAR-10에서 54개의 2-layer Residual unit을 가진 ResNet-110으로 진행했다.
Random variation을 방지하기 위해 5번 실행 후 median accuracy를 얻었다.

위의 연구에서는 identity f를 말했지만, 이 실험은 f=ReLU이다(identity f는 추후 사용할 예정).
기본 ResNet-110의 test error는 6.61%이다.

결과는 다음과 같다.

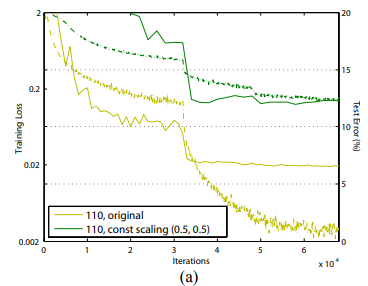
Constant scaling

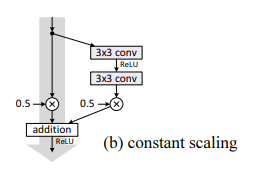
모든 shortcut에 대해 $\lambda=0.5$를 적용했고 case를 2개로 나눴다.

• $\mathcal{F}$ 그대로 -> 수렴하지 않았다.
• $\mathcal{F}$에 $1-\lambda=0.5$ 적용, 수렴했으나 12.35%의 error가 발생했다.

즉 shortcut signal $h(x)가 scale down된 경우, 최적화가 어려웠다.

Exclusive gating

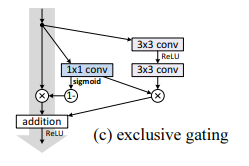
Gating 함수(RNN에 사용되는 것과 동일한듯) $g(x)=\sigma(W_gx+b_g)$를 사용했다($\sigma$=시그모이드 함수).
Convolutional network라서 g(x)는 conv1x1이고, 이후 element-wise multiplication으로 적용했다.
(아마도 $W_gx+b_g$를 conv1x1로 하고, sigmoid를 했다는 듯)
g(x)는 scalar값이다.

• $\mathcal{F}$에는 g(x)로 scaling
• Shortcut은 1-g(x)로 scaling

Bias $b_g$가 중요하기에 0~-10까지 -1씩 하며 cross-validation한 결과, -6가 best였다.
(참고로 Table 1을 보면 $b_g$가 제대로 설정되지 않으면 결과가 안 좋은 것을 볼 수 있다)
8.7%의 test error(Table 1)을 얻었는데, 이는 여전히 original보다 좋지 않다.

1-g(x)가 1로 가면 shortcut이 identity function이 되는 효과가 있다.
그렇지만 이는 g(x)가 0으로 간다는 말이므로 $\mathcal{F}$가 suppress되어 좋지 않다.
따라서 non-exclusive gating mechanism을 탐구했다(suppress 안하기 위해서!).

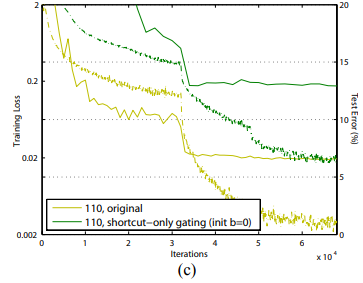
Shortcut-only gating

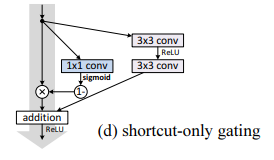
• $\mathcal{F}$는 not scaled
• Shortcut은 1-g(x)로 scaling

bias $b_g$의 초기화 역시 중요했다.

• $b_g$가 0일때, 12.86%라는 좋지 않은 test error가 나왔다.
  Training error도 높았다.
• $b_g$가 -6과 같은 큰 negative일 때, 1-g(x)는 1에 가까워져 identity mapping처럼 작동했고,
  그 결과 6.91%의 test error가 나왔다.
  

1x1 convolutional shortcut

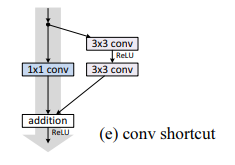
기존 ResNet 논문(34 layer)에서 conv1x1도 shortcut에 적용하면 유용하다고 했다.
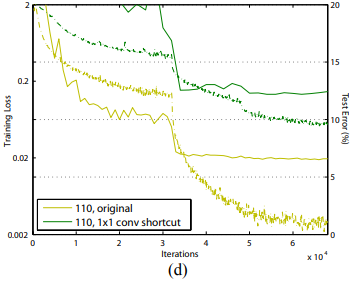
다만 실험 결과, layer가 많으면(110) 12.22% test error라는 좋지 않은 결과를 냈다.
Training error 역시 높았다.
이는 가장 짧은 path조차도 신호 전파를 방해했다.
이러한 현상은 ImageNet에서 ResNet-101을 이용했을때도 마찬가지였다.

Dropout shortcut

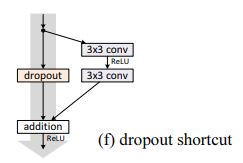
Dropout(ratio=0.5)를 identity shortcut의 output에 적용했으나 수렴하지 못했다.
Dropout은 constant scaling($\lambda=0.5$)하는 효과를 가져왔으며, 신호 전파를 방해했다.

3.2 Discussions

Multiplicative(conv1x1, gating, scaling, dropout, 곱셈을 기반으로 하는 연산을 말하는듯) 조작은 정보 전파를 방해하고 최적화 문제를 일으킨다.

사실 gating, conv1x1은 parameter가 더 많아서 representational ability가 더 강하다.
그래서 identity shortcut으로도 최적화될 수 있었다
(마치 2차원 함수가 1차원 함수로 mapping되듯이).

그러나 성능이 identity shortcut보다 좋지 않은 것으로 보아, degradation 문제는 representational power 문제가 아니라 최적화 문제인 것이다.

4. On the Usage of Activation Functions

위의 실험은 f를 identity라 가정한 수식을 기반으로 했지만 실제로는 "ReLU"를 사용했다.
즉, 근사치로 수식을 증명한 것이다.
따라서 Section 4에서는 f에 대해서 탐구할 것이다.

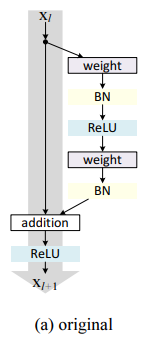
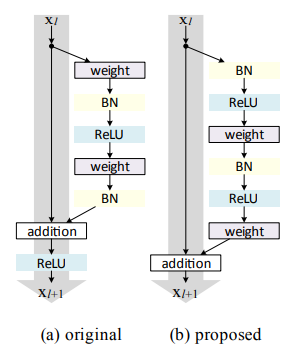
Fig. 4(a)를 보면 기존에 사용한 Residual Unit이 있다.
Weight(conv3x3)-BN-ReLU-Weight(conv3x3)-BN-addition with shortcut-ReLU
의 단계를 따르고 있다.
이제 이를 변형해보겠다.

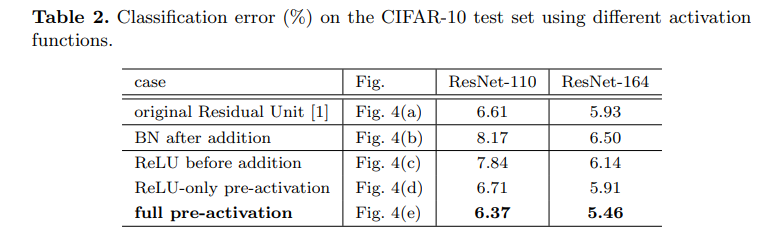
4.1 Experiments on Activation

ResNet-110과 164-layer BottleNeck 구조를 사용했다.
둘 다 비슷한 컴퓨팅 복잡도를 가지고 있으며, CIFAR-10에서 test error는 각각 6.61%/5.93%이다.

BN after addition

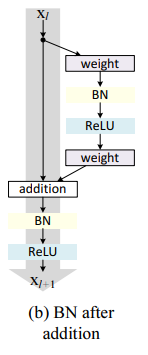
f를 identity function 만들기 전에, f=BN+ReLU로 만들었다.
그러나 결과는 더 나빠졌다.
이는 BN이 shortcut의 정보 전달을 방해해서 그런 듯하다.

ReLU before addition

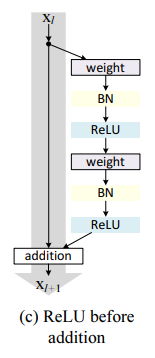
f를 identity function으로 만드는 가장 단순한 방법은 ReLU를 addition 전으로 옮기는 것이다.
그러나, ReLU는 값을 $[0, \infin)$으로 만든다.
Residual unit은 ($-\infin, +\infin$)를 받아야 하는데 그렇지 못해서, forward 신호가 monotically increasing(단조 증가)한다.
이 때문에 representational ability가 영향을 받아 error가 더 커졌다(7.84%).

다음 실험부터는 residual function(shortcut 말고 옆에 빠진 부분)이 $(-\infin, +\infin)$의 값을 갖도록 할 것이다.

내 방식대로 정리
물론, addition 후에도 ReLU를 통해 다음 layer의 input이 $[0, \infin)$가 된다.
그러나, shortcut은 [0, $\infin$)라 할지라도, residual function은 conv layer를 통과하며
값의 범위가 $(-\infin, +\infin)$가 된다.
즉, shortcut + residual function의 범위도 $(-\infin, +\infin)$가 된다.
그래서 더 다양한 값을 표현할 수 있는 것이다.
그렇지만, 만일 ReLU가 residual function 끝에 있다면?
Shortcut과 residual function 결과값 모두 $[0, \infin)$이다.
즉, 표현할 수 있는 범위가 절반이 되는 것이다.
물론 이걸로만 해도 충분은 하지만, 그래도 범위의 감소가 representational ability에 영향력을 준다고 보는 것이다.

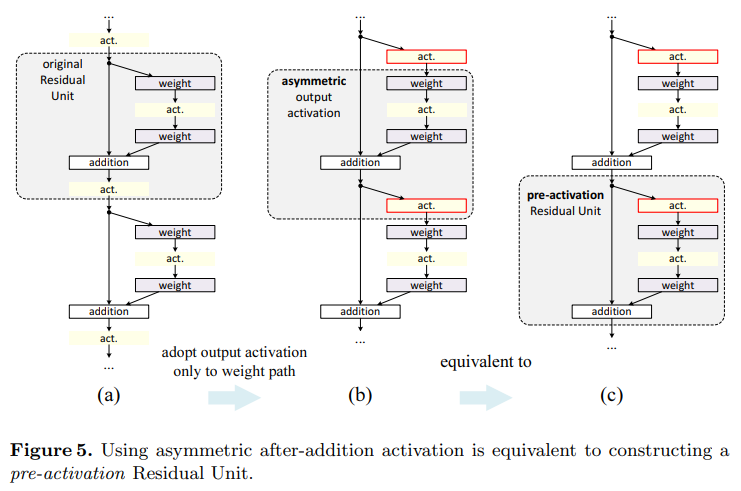
Post-activation or pre-activation?

만일 activation이 $\mathcal{F}$에만 영향을 준다면 어떨까?

유도해보자.
기존 : $y_l = x_l + \mathcal{F}(x_l, \mathcal{W}_l)$, $x_{l+1}=f(y_l)$
식을 보면 알 수 있듯이, $y_l$은 activation 전 값, $x_l$은 activation 이후의 값이다.
$x_l$을 residual unit의 input, output으로 보면 된다.
$y_{l+1}=x_{l+1}+\mathcal{F}(x_{l+1}, \mathcal{W}_{l+1})$이고, 대입하면
$y_{l+1}=f(y_l)+\mathcal{F}(f(y_l), \mathcal{W}_{l+1})$이 된다.
여기서 $\mathcal{F}$에만 activation이 있으므로
$y_{l+1}=y_l+\mathcal{F}(\hat{f}(y_l), \mathcal{W}_{l+1})$ - (1) 이 된다.
이를 renaming하면
$x_{l+1}=x_l+\mathcal{F}(\hat{f}(x_l), \mathcal{W}_{l})$ - (2) 이 된다.
사실 수식이 직관적으로 이해되지는 않았다.
(1) -> (2)의 과정이 ?? 싶었다.
그렇지만 Fig.5(a), (b)를 보면 asymmetric form을 만들어서 수식을 새롭게 정의한 듯 하다.

그래서 $W_{l+1}$이 $W_l$이 된 것 아닐까? Residual unit 범위를 새로 지정했기 때문에..
왜 activation이 맨 앞에 있나요? 에 대한 답변은 이전 실험에서 ReLU before addition이 좋지 않은 결과를 내어 제외되었기 때문이다.
사실 Activation이 post인지 pre인지는 plain network에서는 큰 상관이 없다.
그러나 branch로 만들 것이라면 얘기가 다르다.

이 된다.
이 수식은 $x_L = x_l + \sum_{i=1}^{L-1}\mathcal{F}(x_i, \mathcal{W}_i)$과 비슷하게 생겼다.
즉, identity activation이 된다는 것이다.

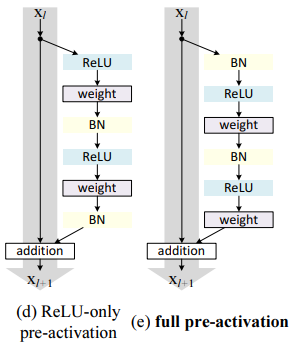
Activation을 2개로 나눠 실험했다.

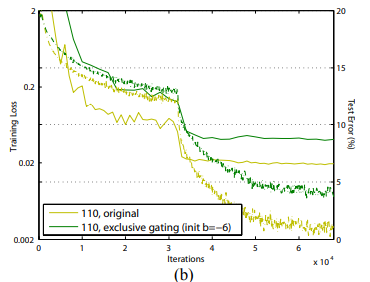
• Pre-activation에 오직 ReLU만 있는 경우(ReLU-only pre-activation)
  이 경우는 BN의 이점을 살리지 못한다. 그래서 결과가 base 모델과 비슷했다.
• Pre-activation에 ReLU, BN 같이 쓰는 경우(full pre-activation)
  이 경우에 성능이 드디어 발전했다! Table 2, 3에 결과가 정리되어있다.
  CIFAR-10,100에서 ResNet-110, ResNet-110(Residual unit = 1 layer), ResNet-164, BottleNeck-1001로 실험했다.
  모든 경우에서 base 모델보다 full pre-activation이 더 좋은 성능을 보여줬다.

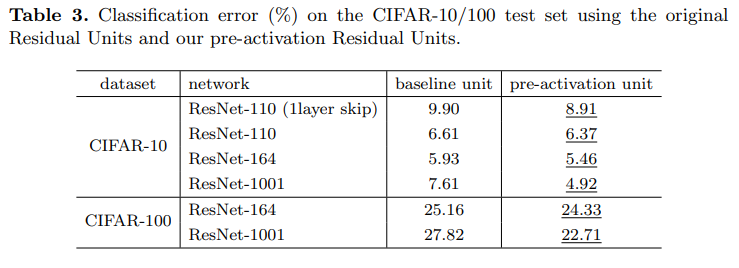
4.2 Analysis

Pre activation은 최적화를 쉽게 하고, 규제 효과가 있다.

Ease of optimization

BottleNeck 1001-layer에서 Fig. 1을 보면 알 수 있듯이, training error가 매우 천천히 감소한다.

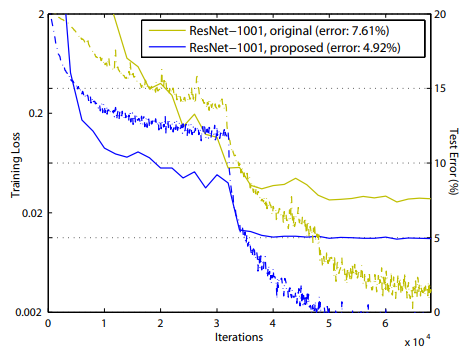
이는 f가 ReLU라서 그렇다.
ReLU는 음수 신호일 때 영향 받는데, 또 layer가 많기에 identity activation이라고 근사할 수 없다.
그러나 진짜로 identity activation을 쓰면, training loss가 매우 빠르게 감소하고 loss 역시 최저치를 달성했다.

기본 구조 수식 : $y_l = x_l + \mathcal{F}(x_l, \mathcal{W}_l), x_{l+1} = f(y_l)$
기본 구조는 layer가 적을때는 f가 ReLU여도 처음에만 잘 안되고 추후에는 안정화된다.
이는 ReLU가 $x_l$을 non-negative하게 만들어도, $y_l$도 음수가 되려면 $\mathcal{F}$의 값이 0보다 한참 작아야해서 그렇다.
만일 $y_l$이 음수가 되면 f(ReLU)에 의해 다음 residual unit input이 0이 될 것이다.
(즉, ReLU가 음수값을 0으로 만들어서 영향을 주긴 하지만, layer가 적으면 그렇게 잘 안되니까 영향을 덜 받는다는 얘기)

그렇지만 layer가 많아지면 truncate가 더 많아진다.
(truncate : 신호가 잘리는 것, 여기서는 ReLU로 인해 음의 값이 사라지는 현상을 의미)

Reducing overfitting

또 pre-activation은 규제 효과가 있다(Fig. 6(right)).

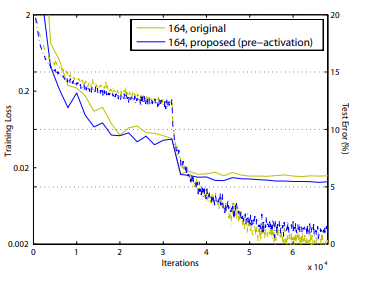
Training loss는 더 높지만, test error는 더 낮다.
이는 규제가 잘 작동함을 보여준다.
이러한 현상은 CIFAR-10,100에서 ResNet-110, 110(1 layer), 164에서 관찰되었다.

그 원인은 다음과 같이 추측된다.
기존에는 BN 후 shortcut을 더했기에, 다음 unit input이 normalize되지 않았다.
그렇지만 지금은 shortcut까지 addition한 후, 다음 unit 내에서, weight 바로 직전에 BN 하므로,
input이 normalized된다.
따라서 BN의 규제 효과를 얻을 수 있다.

5. Result

Comparisons on CIFAR-10/100

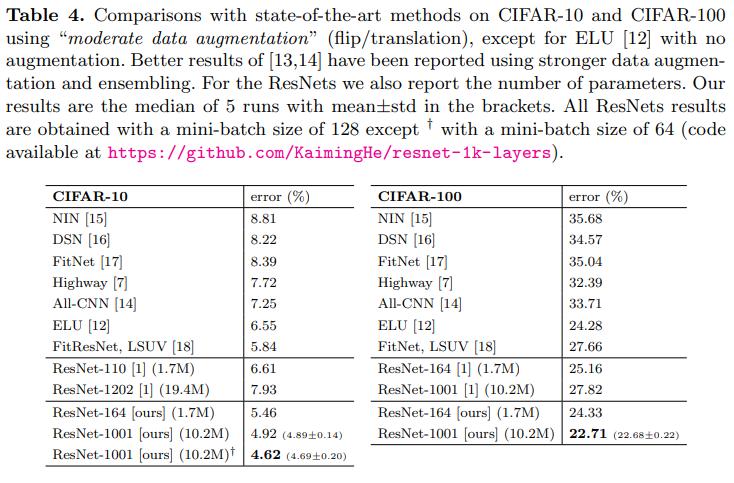
Table 4는 CIFAR-10/100에서의 SOTA 성능을 비교한다.
Filter size, network width는 건드리지 않고, 규제(dropout같은 것, small dataset에서 유용함)도 사용하지 않았다.
오직 "going deeper"에만 집중했다.

Comparisons on ImageNet

앞서 conv1x1을 이용한 실험에서 사용한 ResNet-101은 ImageNet에서 최적화문제가 있었다.
Non-linearity shortcut(아마도 conv1x1)을 가진 ResNet-101은 학습을 중단해야할 정도였다.
ResNet-101(BN after addition)은 ImageNet에서 학습은 가능했으나, 높은 training loss와 validation loss를 보여줬다.
이 모델의 single crop(224xx224) validation error는 24.6%/7.5%였다.
(아무것도 하지 않은 ResNet-101은 23.6%/7.1%이다. 즉 BN after addition이 결과가 더 안 좋았다)
(참고로 CIFAR에서 쓴 BN after addition은 ResNet-110이다. 헷갈리지 말자.)

Table 5는 ResNet-152, 200의 결과를 보여준다(각각 바닥부터 학습했다).

Original ResNet 논문은 scale gittering(s=[256, 480])을 했고,
그래서 224x224 crop, s=256으로 한 test는 negative biased였다.
(근데 ResNet에서 scale jitter했나..? 안 했던 것 같은데..)

대신, 320x320 crop(s=320, so original image)으로 훈련했다.
ResNet은 Fully Convolutional한 구조라서 더 작은 crop에서 학습되어도 무관하다.
(참고로 이 사이즈는 Inception v3의 299x299와 비슷해서 비교할만하다)

기존의 ResNet-152는 21.3%, Pre-activation ResNet은 21.1%이다.
차이가 얼마 나지 않는 것은, 기존 모델도 일반화에 딱히 큰 문제가 없었기 때문이다.

ResNet-200은 21.8%로 ResNet-152보다 높다.
그렇지만, Pre-activation ResNet-200은 20.7%로, Pre-activation ResNet-152보다도 낮다.
Scale, aspect ratio augmentation까지 하면 Pre-activation ResNet-200은 Inception-v3보다도 나은 결과를 보여준다(20.1%/4.8% vs 21.2%/5.6%).

다만 Inception-ResNet-v2에는 못 미치는 결과(19.9%/4.9%)를 가지고 있다.

그렇지만 이러한 Residual Unit은 다른 ResNet에도 도움될 것이다.

Computational Cost

Pre-activation 모델은 컴퓨팅 복잡도가 깊이에 비례한다.
그래서 1001-layer는 대략 100-layer의 10배이다.

CIFAR에서는 ResNet-1001이 2GPU로 27시간 학습했고,
ImageNet에서는 ResNet-200이 8GPU로 약 3주간 학습했다.

6. Conclusions

이 논문은 propagation formulaton에 대해 연구해, identity shortcut connection과 identity after-addition activation의 필요성을 보여준다.

또한 1000-layer deep network도 쉽게 학습되고 높은 정확도를 얻을 수 있음을 보여준다.