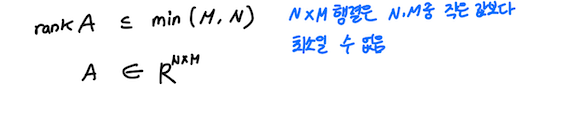1. 랭크 (Rank)
열랭크 (column rank)
: 행렬의 열벡터 중 서로 독립인 열벡터의 최대 개수
행랭크 (row rank)
: 행렬의 행벡터 중 서로 독립인 행벡터의 최대 개수
이때 주의할 점!
랭크 = 행랭크 = 열랭크
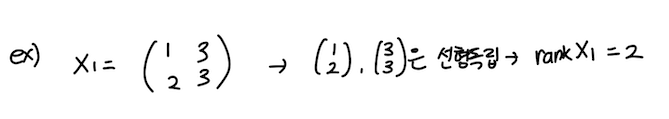
2. 풀랭크 (full rank)
: 랭크가 행의 개수와 열의 개수 중 작은 값과 같은 경우
rankA = min(N, M)
선형독립인 벡터들을 열 & 행으로 가지면 항상 풀랭크
예제) 랭크 구하기
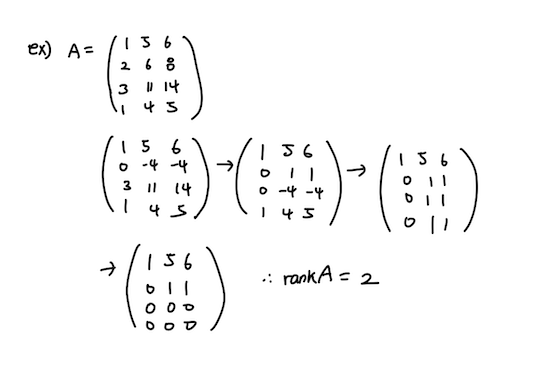
위의 경우 rankA = 2 -> 풀랭크 아님
3. 로우-랭크 행렬 (low-rank matrix)
rank-1 matrix : N차원 벡터 x 하나를 이용하여 만들어지는 행렬
rank-2 matrix : 선형독립인 2개의 N차원 벡터 x1, x2를 이용해서 만든 행렬
rank-m matrix : 선형독립인 M개의 N차원 벡터 x1, x2, …, xm을 이용해서 만든 행렬
ex) x1, x2가 아래와 같을때 rank-2 matrix의 랭크가 2인 것을 확인하기
데이터 사이언스 스쿨
위의 링크를 참고하여 학습했습니다. 좋은 자료 감사합니다!