[선형대수학] 벡터(2)

1. 유클리드 거리

: 두 벡터가 가리키는 점 사이의 거리

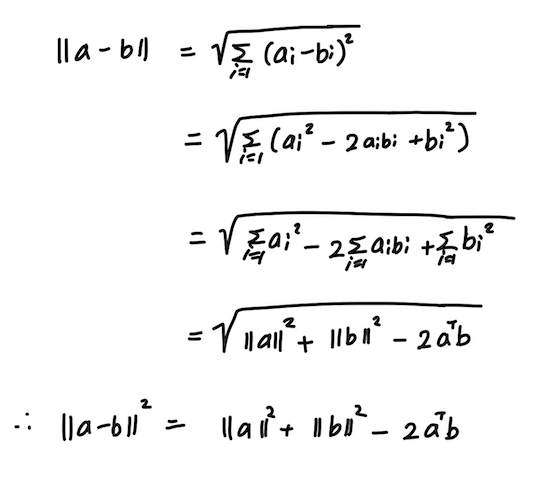
2. 삼각함수

: 사인&코사인 함수


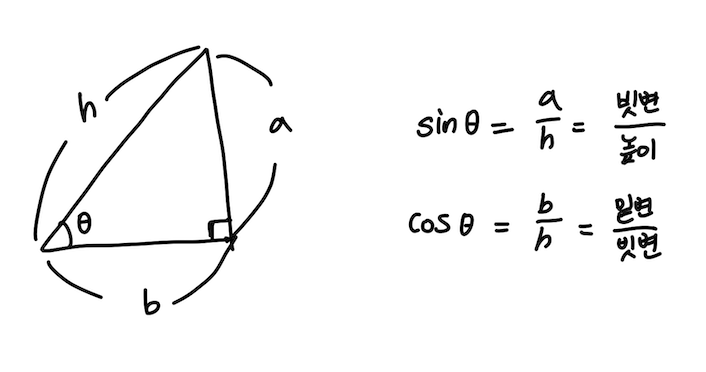
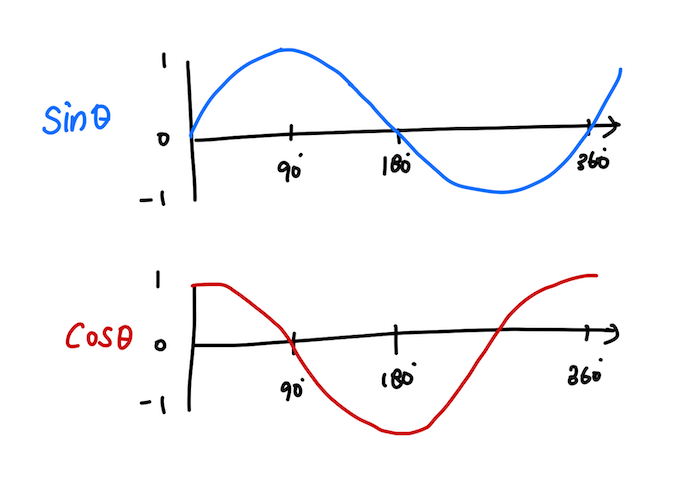
sin𝜃 는 0에 가까워질수록 0에 가깝고, 90에 가까워질수록 1에 가까워짐
cos𝜃 는 0에 가까워질수록 1에 가깝고, 90에 가까워질수록 0에 가까워짐

3. 벡터의 내적

: 𝑎^𝑇𝑏=‖𝑎‖‖𝑏‖cos𝜃

4. 직교

: 두 벡터 a,b가 이루는 각이 90도 = orthogonal = a⊥b

이때, 두 벡터의 내적은 0 (cos90= 0이기 때문)

5. 정규직교

: N개의 단위벡터 𝑣1,𝑣2,⋯,vN 가 서로 직교
‖𝑣𝑖‖=1
𝑣𝑖^T𝑣𝑗=0(𝑖≠𝑗)

6. 코사인 유사도

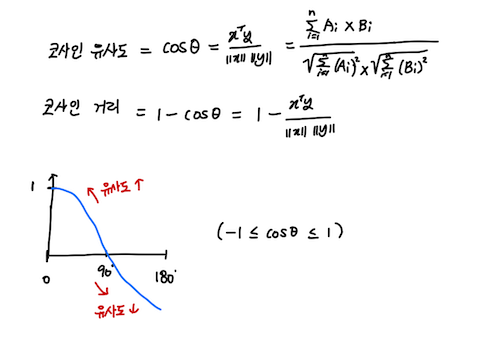
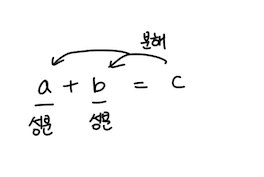
7. 벡터의 분해와 성분

: 어떤 두 벡터 a, b의 합이 다른 벡터 c가 될 때 c가 두 벡터 성분(component) a, b으로 분해(decomposition)된다고 말함

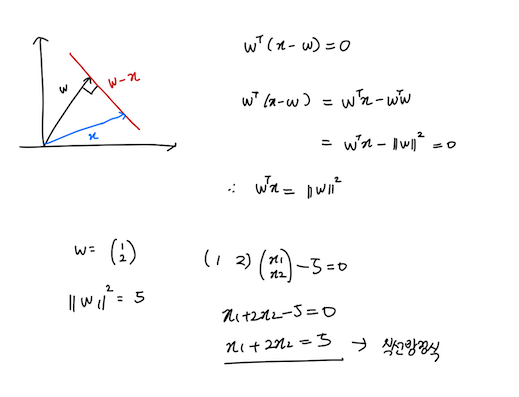
8. 직선의 방정식

: 원점에서 출발한 벡터w를 지나면서 w에 수직인 방정식 구하기

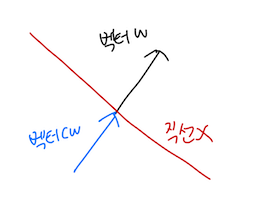
: 원점 출발 조건 없이 벡터w에 수직인 직선방정식 구하기

데이터 사이언스 스쿨
위의 링크를 참고하여 학습했습니다:)