[LeetCode] 2130. Maximum Twin Sum of a Linked List

1. Question

In a linked list of size n, where n is even, the ith node (0-indexed) of the linked list is known as the twin of the (n-1-i)th node, if 0 <= i <= (n / 2) - 1.

For example, if n = 4, then node 0 is the twin of node 3, and node 1 is the twin of node 2. These are the only nodes with twins for n = 4.
The twin sum is defined as the sum of a node and its twin.

Given the head of a linked list with even length, return the maximum twin sum of the linked list.

Example 1:

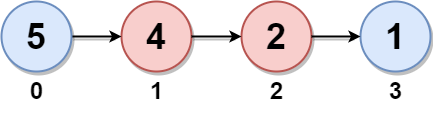
Input: head = [5,4,2,1]
Output: 6
Explanation:
Nodes 0 and 1 are the twins of nodes 3 and 2, respectively. All have twin sum = 6.
There are no other nodes with twins in the linked list.
Thus, the maximum twin sum of the linked list is 6. 

Example 2:

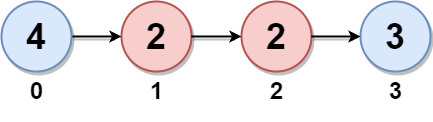
Input: head = [4,2,2,3]
Output: 7
Explanation:
The nodes with twins present in this linked list are:
- Node 0 is the twin of node 3 having a twin sum of 4 + 3 = 7.
- Node 1 is the twin of node 2 having a twin sum of 2 + 2 = 4.
Thus, the maximum twin sum of the linked list is max(7, 4) = 7. 

Example 3:

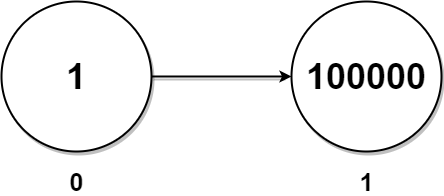
Input: head = [1,100000]
Output: 100001
Explanation:
There is only one node with a twin in the linked list having twin sum of 1 + 100000 = 100001.

2. Thoughts

1. Get the length of the linked list
2. Traverse first_half till the middle of the ll
3. Make the first_half reverse (reverse "next")
4. Add first_half and second half( second half will be regular way of from the middle)

3. Tips learned

4. My solution

class Solution:
    def pairSum(self, head: Optional[ListNode]) -> int:
        total_counter = head
        count = 0
        while total_counter:
            count += 1
            total_counter = total_counter.next

        count //= 2

        prev = None
        current = head

        while count > 0:
            nexts = current.next
            current.next = prev
            prev = current
            current = nexts

            count -= 1

        result = 0
        while current:
            result = max(result, current.val + prev.val)
            current = current.next
            prev = prev.next

        return result

46/46 cases passed (585 ms)
Your runtime beats 89.19 % of python3 submissions
Your memory usage beats 90.21 % of python3 submissions (38 MB)

5. AI Solution and Improvements

Your solution to find the maximum twin sum in a linked list is well-structured and effectively addresses the problem. However, it can be slightly optimized and simplified. Here's an improved version of your solution:

Optimized Solution

1. Find the Middle of the List and Reverse the First Half: This is similar to what you've done, but we can merge the counting and reversing into a single pass, which reduces the code complexity.

2. Compare and Find Maximum Twin Sum: Traverse the two halves simultaneously and calculate the twin sums, updating the maximum as you go.

Here's the revised code:

class Solution:
    def pairSum(self, head: Optional[ListNode]) -> int:
        # Step 1: Find the middle and reverse the first half
        slow, fast = head, head
        prev = None
        while fast and fast.next:
            fast = fast.next.next
            nexts = slow.next
            slow.next = prev
            prev = slow
            slow = nexts

        # Step 2: Calculate max twin sum
        max_sum = 0
        while slow:
            max_sum = max(max_sum, slow.val + prev.val)
            slow = slow.next
            prev = prev.next

        return max_sum

Explanation

• Finding the Middle: The slow and fast pointers are used to find the middle of the list. The slow pointer moves one step at a time, while the fast pointer moves two steps. When the fast pointer reaches the end, the slow pointer will be at the middle.

• Reversing the First Half: As we move the slow pointer, we also reverse the first half of the list. This is done by manipulating the next pointers of the nodes.

• Calculating the Maximum Twin Sum: Once the list is split and the first half is reversed, we traverse the two halves simultaneously and calculate the twin sums, updating the maximum sum accordingly.

Benefits of the Improved Solution

• Efficiency: The number of traversals through the list is reduced, making the solution more efficient.
• Simplicity: Combining the counting and reversing steps makes the code more concise and easier to understand.
• Readability: The use of slow and fast pointers is a common technique in linked list problems, making the solution more recognizable to those familiar with such patterns.