[LeetCode] 328. Odd Even Linked List

1. Question

Given the head of a singly linked list, group all the nodes with odd indices together followed by the nodes with even indices, and return the reordered list.

The first node is considered odd, and the second node is even, and so on.

Note that the relative order inside both the even and odd groups should remain as it was in the input.

You must solve the problem in O(1) extra space complexity and O(n) time complexity.

Example 1:

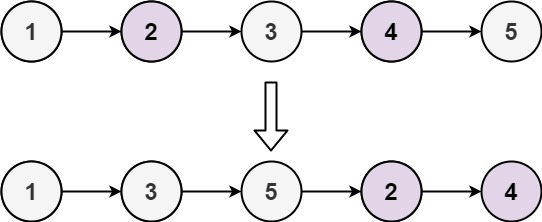
Input: head = [1,2,3,4,5]
Output: [1,3,5,2,4]

Example 2:

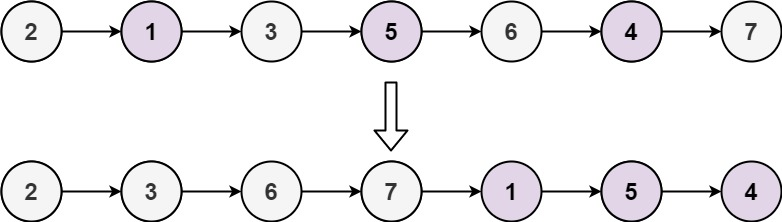
Input: head = [2,1,3,5,6,4,7]
Output: [2,3,6,7,1,5,4]

2. Thoughts

3. Tips learned

4. My solution

class Solution:
    def oddEvenList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        if not head or not head.next:
            return head

        odd = head
        even_start = head.next
        even = head.next
        while odd.next and even.next:
            odd.next = odd.next.next
            even.next = even.next.next
            odd = odd.next
            even = even.next

        odd.next = even_start
        return head

70/70 cases passed (47 ms)
Your runtime beats 59.21 % of python3 submissions
Your memory usage beats 6.77 % of python3 submissions (19.1 MB)

5. AI Solution and Improvements

Your solution is already optimal for the given problem. It effectively groups nodes with odd and even indices together while maintaining their relative order. Furthermore, your solution meets the requirements of ( O(1) ) extra space complexity and ( O(n) ) time complexity. Here's a breakdown of how your code accomplishes this:

1. Edge Case Handling: You correctly handle cases where the list is empty or has only one node.
2. Separation of Odd and Even Nodes: You use two pointers, odd and even, to traverse and separate the nodes.
3. Linking Odd and Even Lists: After the separation, you connect the end of the odd list to the head of the even list.
4. Traversal and Link Adjustments: During traversal, you adjust the links such that all odd-indexed nodes are connected together and all even-indexed nodes follow them.

Here is a slightly refined version of your code for better readability, although the logic remains the same:

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

class Solution:
    def odd_even_list(self, head: ListNode) -> ListNode:
        if not head or not head.next:
            return head

        # Initialize pointers for odd and even nodes
        odd, even = head, head.next
        even_start = even

        # Traverse the list and rearrange the odd and even nodes
        while even and even.next:
            odd.next = odd.next.next
            even.next = even.next.next
            odd = odd.next
            even = even.next

        # Connect the end of the odd list to the start of the even list
        odd.next = even_start

        return head

This code is essentially the same as yours with some minor adjustments for clarity. The performance and complexity remain optimal for the problem statement.