Denoising Diffusion Probabilistic Models

Diffusion Probabilistic model과 denoising score matching을 연결하여 Image 생성 모델 제시

1. Introduction

---

기존의 생성모델로 제시 되었던 GAN과는 다르게 energy-based modeling과 score matching의 발전은 더 높은 품질의 이미지를 생성했다.

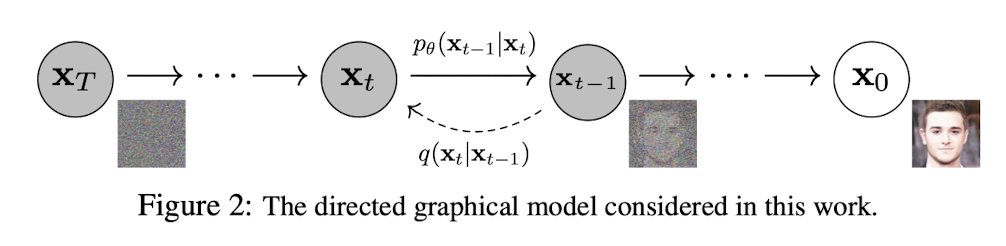
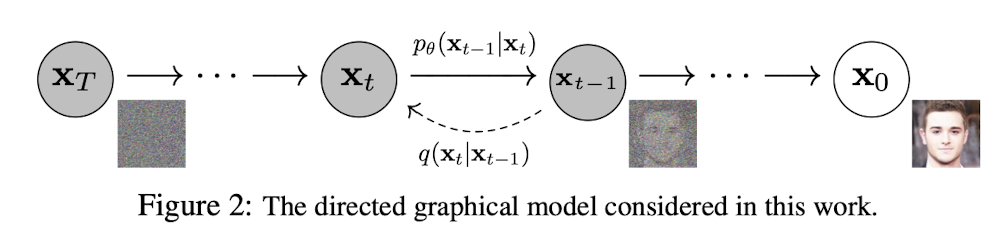
이 논문에서는 위 figure와 같이 Diffusion model의 과정을 보여준다. 원본 데이터에 점진적으로 Gaussian noise를 추가해가면서, 최종 timestep인 T에서 데이터는 $N(0, I)$의 분포를 가지는 Gaussian Noise가 된다. Diffusion model은 최종적으로 위 분포를 가진 noise를 denoising하여 원본 데이터 $x_0$을 만드는 과정을 학습하여, noise에서 높은 품질의 데이터를 생성할 수 있다.

2. Background

---

Diffusion model은 원본 데이터($x_0$)에서 점진적으로 Markov chain에 따른 gaussian noise를 더하여 최종적으로 $N(x_t; 0, I)$ 분포의 noise로 만드는 forward process와 표준정규분포를 따르는 noise ($x_T$)에서 $x_0$를 추정해 나가는 reverse process로 나눌 수 있다. 식 (1)과 (2)는 각각 backward, forward process를 표현한 식이다.

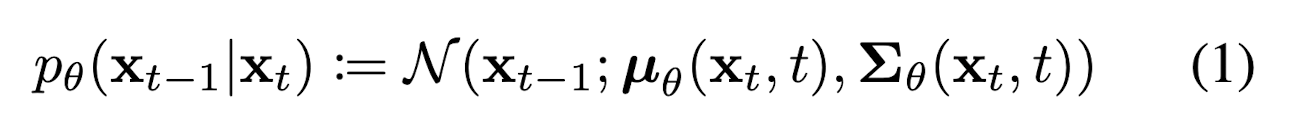
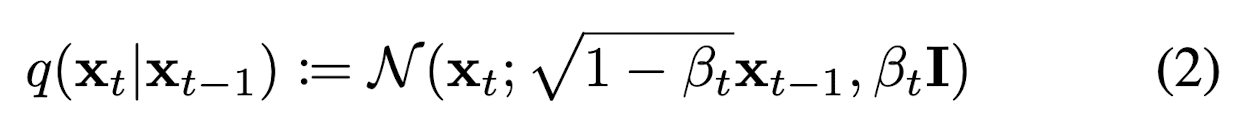
식 (1)의 $p_{\theta}$는 모델이 학습해야하는 파라미터로, diffusion model이란 결국 뒤 시간에 있는 데이터 (더 noisy)를 바탕으로 앞쪽의 시간에 있는 데이터 (덜 noisy)의 분포를 추정하는 모델인 것이다.
식 (2)의 forward pass에서는 $\beta_t$ 분산에 따른 Gaussian noise를 t-1시점의 데이터에 더하여 t시점의 data 생성하는 것을 확인할 수 있다. Forward pass에서의 $\beta_t$는 학습하여 parameter로 사용할 수 있고, 동시에 상수로써 hyperparameter로도 사용될 수 있으나, 본 논문에서는 t가 증가함에 따라 선형적으로 증가하는 상수로 정의하고 사용하였다.

위 과정을 합하여 최종적으로 훈련중에 모델이 optimize 해야할 식은 아래와 같다.

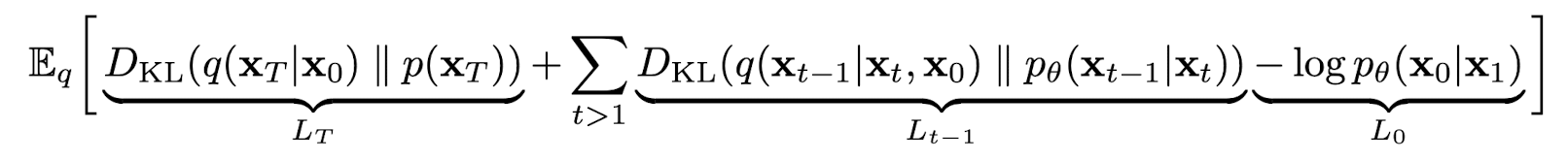
$x_T$는 표준정규분포를 띄는 가우시안 노이즈 이고 forward pass에서 더해지는 noise는 고정적인 값이므로 위 Loss에서 $L_T$와 $L_0$는 상수로 취급할 수 있다. 결국 training에서 최소화 해야하는 term은 $L_{t-1}$인데 이는 forward pass에서 추정한 posterior 분포 $q(x_{t-1} | x_t, x_0)$과 학습해야 할 $p_{\theta}(x_{t-1}|x_t)$간의 KL divergance로, 두 분포간의 거리를 최소화 하는 방식으로 학습이 진행된다.

$q(x_{t-1} | x_t, x_0)$는 아래와 같은 방법으로 추정될 수 있다.

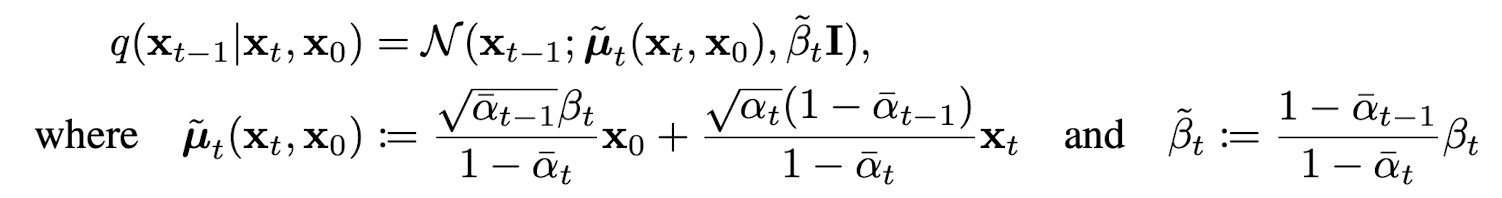
위 식의 핵심은 결국 forward pass의 q에서 $x_t, x_0$을 조건으로 넣어 계산한 $x_{t-1}$의 분포 평균이 $x_0$과 $x_t$의 $\bar {\alpha}$와 $\beta$간의 weighted sum으로 계산할 수 있다는 것이다.

3. Diffusion models and denoising autoencoders

---

본 논문에서는 diffusion model과 denoising score matching간의 새로운 connection을 확립하여, 더 간단한 objective를 제안한다.

Forward process and $L_T$

본 논문에서는 $\beta_t$를 학습하여 parameterize하지 않고, 상수로 고정한다. 따라서 $q$는 학습할 파라미터가 없는 fixed weight 형태이며 그러므로 loss함수에서의 $L_T$ 또한 훈련 중 고려하지 않는다.

Reverse process and $L_{1:T-1}$

Reverse process에서 우리가 찾아야 학습해야 할 $p_{\theta}$는 아래와 같이 정의된다.

먼저 분산인 $\Sigma_{\theta}(x_t, t) = \sigma_t^2 I$로 정의하여 훈련이 필요 없고 시간에 따라 변하는 상수로 정의한다. 위 전제를 바탕으로 $L_{t-1}$을 분포간 거리가 아닌, 두 process에서 평균간의 L2 distance로 간략화 할 수 있다.

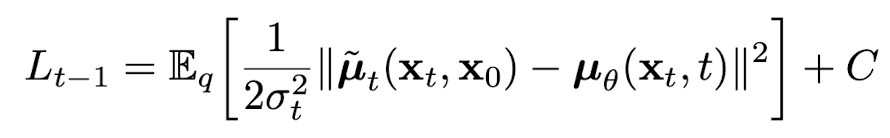
C는 $\theta$에 독립적인 상수로, 결국 모델은 forward process의 posterior로부터 추정된 $\tilde{\mu}_t$를 예측하는 모델이라고 볼 수 있는 것이다. 추가적으로 $x_t$의 sampling 공식인 $x_t(x_0, \epsilon) = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon$ 식을 사용하여 아래와 같은 식을 도출할 수 있다.

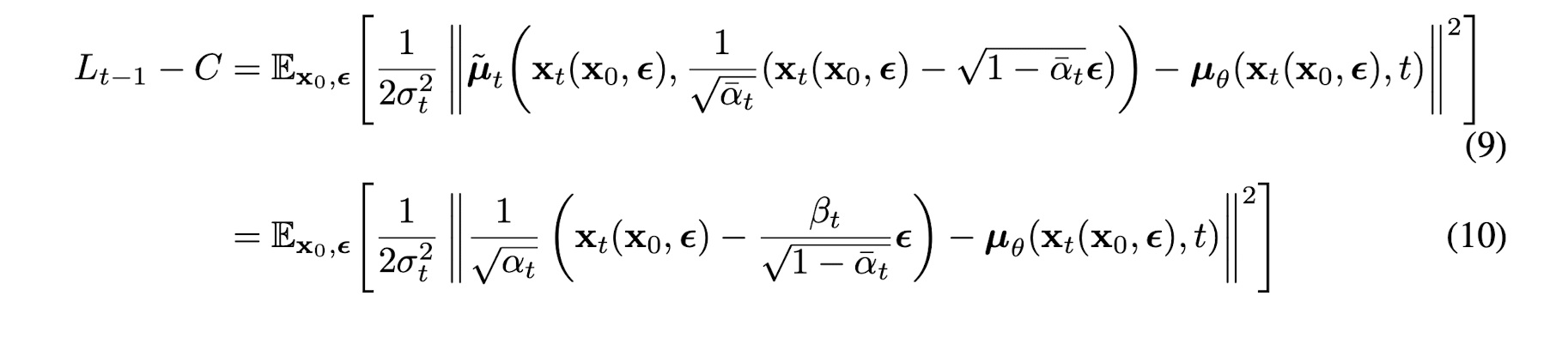
위 식에서 볼 수 있듯이 $\mu_{\theta}$는 결국, $x_t$가 주어졌을 때 forward process에서 $x_{t-1}$에서 $x_t$를 만들 때 사용했던 noise를 예측하는 함수임을 확인할 수 있다. L2 loss 식 안의 좌항에서 의미하는 것은 결국 $x_t$에서 noise를 뺀 데이터의 평균이기 때문이다. 따라서 위 식은 다음과 같이 간략화 될 수 있다.

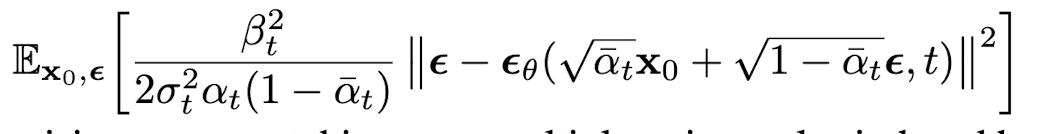
여기서 $\epsilon_{\theta}$는 backward process에서 모델의 추정해야 할 noise이다. 추후에 밝혀지지만 forward posterior의 평균을 추정하는 $\mu_{\theta}$를 사용하여 모델링 하는 것 보다, forward process에서 사용한 noise를 추정하는 $\epsilon_{\theta}$를 사용하여 모델링 하는 것이 더 효율적인 것으로 확인되었다. 추가적으로 t-1에서 t시점으로 가는 foward process에서 사용된 noise를 추정하여, backward process에서 t-1시점의 data를 sampling 할 수 있다.
Training과 Sampling 알고리즘은 아래와 같다.

Training시 사용된 noise와 $x_t$와 t를 사용하여 noise approximation ($\epsilon_{\theta}$)를 구하고, Stochastic Gradient Descent 방법을 사용하여 forward process에 사용된 noise($\epsilon$)간의 차이를 minimize하는 $\theta$를 구한다.
추가로 추정한 $\theta$를 사용하여 backward process에서 $x_{t-1}$을 sampling 할 수 있다.

Data scaling, reverse process decoderm and $L_0$

Image data가 0-255사이의 값으로 이루어져 있고 이들이 [-1, 1]사이의 값으로 scaled되기 때문에, $p(x_T)$로부터 시작된 reverse process가 마지막 stage에서 독립적인 decoder를 거치도록 하였다.

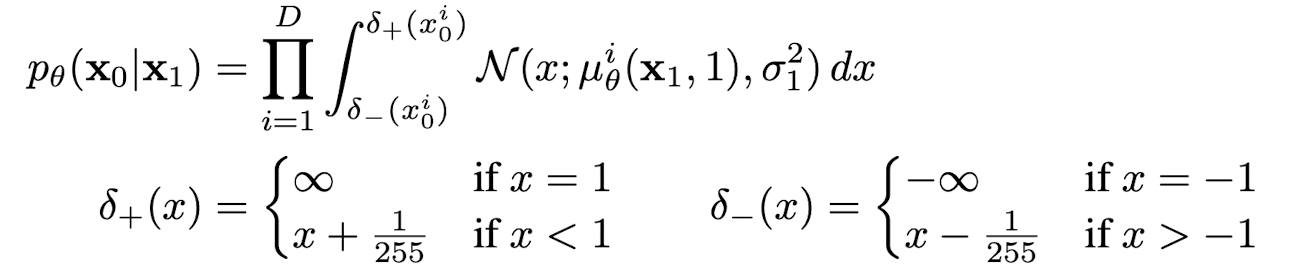
Simplified training objective

Model의 objective function에서 가장 중요한 건 $L_{t-1}$과 $L_0$이다. 본 논문에서는 이를 간단한 형태의 loss form인 $L_{simple}(\theta)$로 정의하였고 이는 아래와 같다.

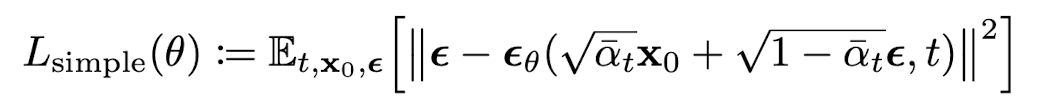
위 식에서 t=1인 경우 $L_0$와 대응되고, t>1인 경우 본래의 $L_{t-1}$loss에서 앞단 weight를 제거한 버전이 되기 때문에 간단하게 이용할 수 있고 이를 통해 매우 작은 t에서뿐만 아니라, 큰 t에 대해서도 network 학습이 가능하기 때문에 효과적이라고 본 논문에서는 서술하고 있다.

4. Experiments

---

모든 실험에 대해 T값을 1000으로 고정시켰고, $\beta$는 $10^-4$에서 0.02로 T가 증가하면서 선형적으로 변하도록 하였다. 이 고정값은 reverse과 forward process가 $x_T$에서 최대로 작은 SNR을 유지하도록 보장하였다.

또한 reverse process에서 U-Net backbone을 사용하였고 Transformer sinusoidal position embedding을 통해 parameter가 t에 거쳐 공유되도록 하였다.

Sample quality

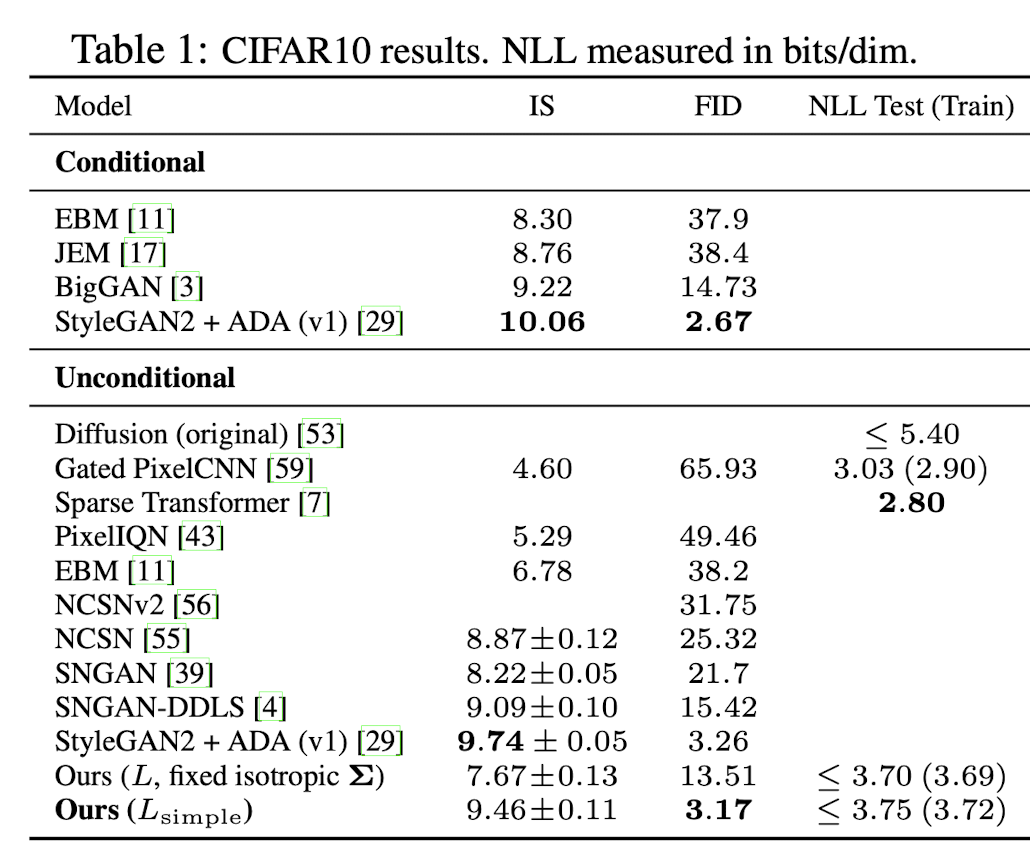
본 논문에서 제시한 방법, 즉 $L_{t-1}$을 간단하게 하여 사용하는 것이 loss term을 그대로 사용하는 것보다 더 좋은 퀄리티의 이미지를 출력한다는 것을 확인할 수 있다.

Reverse process parameterization and training objective ablation

Loss를 optimize시 $\mu_{\theta}$를 추정하는 것 보다 $\epsilon_{\theta}$를 추정하는 것이 simple loss를 사용하는 경우 더 좋은 성능을 보였다.

Progressive coding

DDPM에서 Progressive coding의 이점은, 각 level(각각의 t시점)에서 data의 representation을 compact하고 효율적으로 만들어 준다는 점이다. forward 과정에서 data의 복잡도를 줄여가면서, 모델은 압축된 형태의 data에서 중요한 정보들을 추출할 수 있고 이는 모델이 높은 차원의 데이터를 생성하고 배울 때 효과적이다.

Interpolation

DDPM의 forward pass에서 encoding 된 두개의 이미지는 model의 latent space에서 interpolation을 수행할 수 있다. interpolated된 latent vector는 DDPM 모델을 통해 Decoding되고, 두 이미지의 특징이 자연스럽게 섞인 새로운 이미지를 생성할 수 있다.