1. PCA

PCA란

• 차원 축소 (dimensionality reduction)과 변수 추출(feature extraction) 기법
• 데이터의 분산을 최대한 보존하면서 서로 직교하는 새 축을 찾아 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법
• 변수를 축소함으로써 과적합과 다중공산성을 방지하고 데이터 수를 줄인다.

방법

1. 각 축의 평균값을 구한 뒤, 해당 점이 중심점(centroid)가 되도록 한다.
   • 각 변수의 평균을 구해서, 모든 데이터에서 빼준다 → 데이터의 중심점(centroid)이 (0,0,…,0)이 되도록 맞춘다.
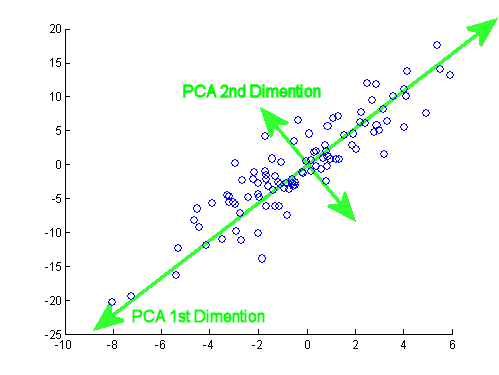
2. 최적의 축 찾기 (PC1)
   • 다양한 방향 (축 후보)에 데이터를 직교 투영해본다.
   • 이때 투영된 점들의 분산이 가장 큰 축을 고른다. 여기서 분산이란, 원점과 투영된 좌표값이 원점과 얼마나 멀리 퍼져있는지이다.
   • 이 축이 제1주성분(PC1)이고, 동시에 원본 점에서 축까지의 직교 거리(오차)를 최소화되는 축과 같다.
3. PC1에 투영
   • 원래 데이터를 PC1 축 위로 직교 투영하면, 1차원 좌표(주성분 점수)가 나온다.
   • 이 점수들은 데이터가 PC1 축을 따라 얼마나 멀리 퍼져있는지를 나타낸다.
4. PC2, PC3, ..
   • PC1과 직교하는 축들 중에서 분산이 가장 큰 축을 찾는다. (PC2)
   • PC2는 PC1이 설명하지 못하는 잔여 변동(Residual Variance)을 설명한다.
   • 같은 방식으로 PC3, PC4..를 찾는다.

2. Python 실습

2.1. 주성분 모델링

import numpy as np
import seaborn as sns

sns.set_style('whitegrid')

rng = np.random.RandomState(13) # Seed 13의 난수 생성기 객체
X = np.dot(rng.rand(2,2), rng.randn(2,200)).T 


X.shape
#결과: (200, 2)

• rng.rand: 2x2 행렬 샘플 생성
• rng.randn: 정규 분포 2x200 행렬 샘플
• np.dot: 행렬곱 -> 정규분포 샘플은 동전 모양의 샘플이 나오므로 PCA 샘플로 적절하지 않아 랜덤한 값들을 곱해준다.

import matplotlib.pyplot as plt

plt.scatter(X[:,0], X[:,1])
plt.axis('equal');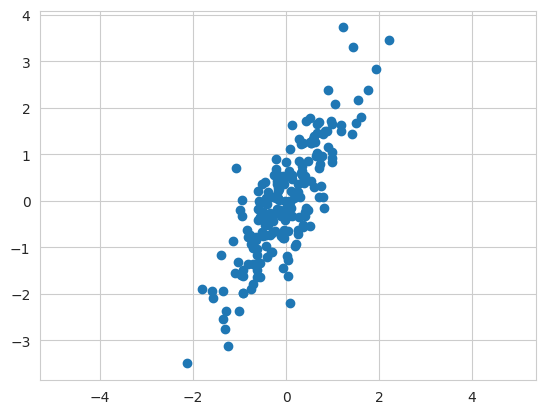

from sklearn.decomposition import PCA


pca = PCA(n_components=2, random_state=13)
pca.fit(X)

n_components: PC 개수

# 벡터
print(f'Vector: {pca.components_}')

#분산
print(f'Explained_variance: {pca.explained_variance_}')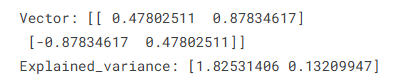

2.2. 주성분 벡터 그리기

def draw_vector(v0, v1, ax = None):
    ax = ax or plt.gca()
    arrowprops = dict(arrowstyle = '->',
                      linewidth = 2,
                      color = 'black',
                      shrinkA=0,
                      shrinkB=0        
    )

    ax.annotate('', v1, v0, arrowprops=arrowprops) 

# annotate에 arrowprops를 사용하면 (x, y)로 이어지는 화살표를 그린다.

plt.scatter(X[:, 0], X[:, 1], alpha=0.4) 

for length, vector in zip(pca.explained_variance_, pca.components_): 
    v = vector * 3 * np.sqrt(length) 
    draw_vector(pca.mean_, pca.mean_ + v) #mean에서 출발해서 벡터 방향으로 오차만큼 뻗어나가는 선 그리기
    

plt.axis('equal');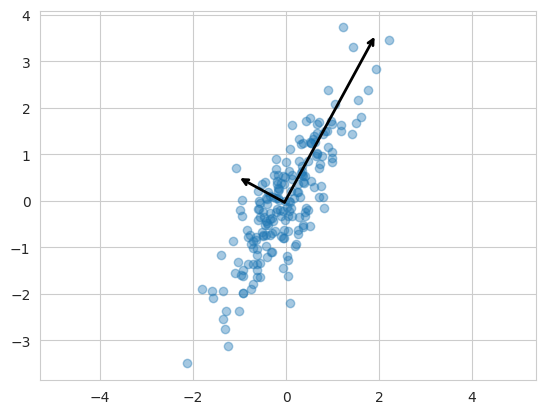

pca = PCA(n_components=1, random_state=13) 
pca.fit(X) 
X_pca = pca.transform(X) #데이터를 새로운 축으로 투영(projection)한 1차원 좌표값을 얻음

pca.explained_variance_ratio_

# 결과: array([0.93251326])

X_new = pca.inverse_transform(X_pca) # 1차원 데이터를 2차원에 표현하기 위해 inverse_transform

plt.scatter(X[:, 0], X[:, 1], alpha=0.4) 
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8) 
plt.axis('equal');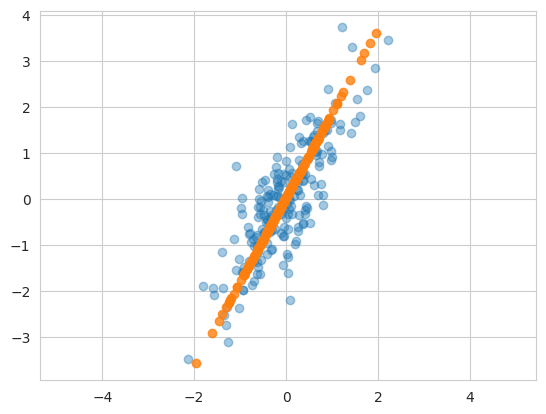

2.3. Iris 데이터 PCA

import pandas as pd 
from sklearn.datasets import load_iris 

iris = load_iris() 

iris_pd = pd.DataFrame(iris.data, columns=iris.feature_names) 
iris_pd['species'] = iris.target 
iris_pd.head()

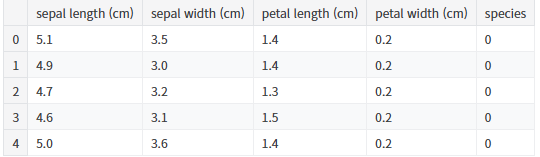
from sklearn.preprocessing import StandardScaler 

iris_ss = StandardScaler().fit_transform(iris.data) 
iris_ss[:5]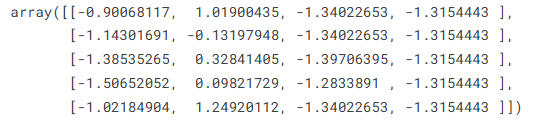

from sklearn.decomposition import PCA 

def get_pca_data(ss_data, n_components=2): 
    pca = PCA(n_components=n_components) 
    pca.fit(ss_data) 

    return pca.transform(ss_data), pca 

iris_pca, pca = get_pca_data(iris_ss, 2) 
print(iris_pca.shape)
print(iris_ss.shape)
print(pca.mean_)
print(pca.components_)

def get_pd_from_pca(pca_data, cols=['PC1', 'PC2']): 
    return pd.DataFrame(pca_data, columns=cols) 

iris_pd_pca = get_pd_from_pca(iris_pca) # 2차원에 투영한 값
iris_pd_pca['species'] = iris.target 
iris_pd_pca.head()

sns.pairplot(iris_pd_pca, hue='species');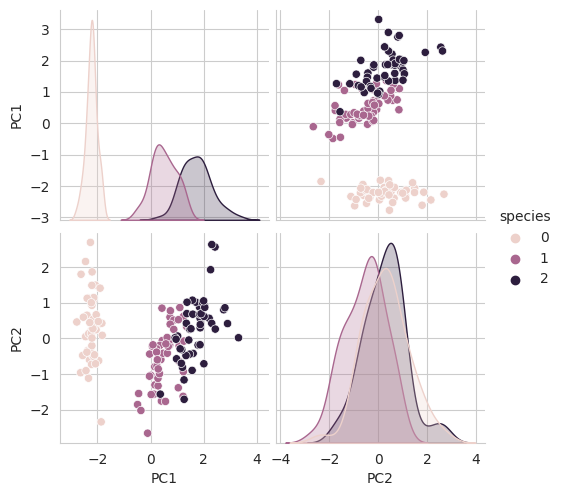 

def print_variance_ratio(pca): 
    print('Explained variance ratio: {}'.format(pca.explained_variance_ratio_)) 
    print('Cumulative explained variance ratio: {}'.format(np.cumsum(pca.explained_variance_ratio_))) 
    
print_variance_ratio(pca) 

Explained variance ratio: [0.72962445 0.22850762]
Cumulative explained variance ratio: [0.72962445 0.95813207]

from sklearn.ensemble import RandomForestClassifier 
from sklearn.model_selection import cross_val_score 

def rf_scores(X, y, cv=5): 
    rf = RandomForestClassifier(random_state=13, n_estimators=100) 
    scores = cross_val_score(rf, X, y, scoring='accuracy', cv=cv) 
    print('CV accuracy scores: {}'.format(scores)) 

rf_scores(iris_ss, iris.target) 

CV accuracy scores: [0.96666667 0.96666667 0.93333333 0.93333333 1. ]