벡터의 내적 (inner product)

Bryant·2025년 10월 21일

수학

목록 보기

7/8

두 벡터 a = (a1, a2, a3)과 b = (b1, b2, b3)의 내적은 다음과 같이 정의된다.

a \cdot b = a_1b_1+a_2b_2+a_3b_3

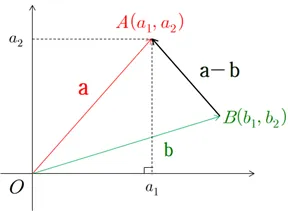
위 그림에서 a-b는 두 벡터의 끝점을 연결하며 이는 삼각형의 변이 된다. a, b, c 세 변을 가지는 삼각형의 코사인 법칙 $c^2 = a^2+b^2-2ab\cdot cos\theta$ 이고 벡터의 크기는 변의 길이이므로

|a-b|^2 = |a|^2 + |b|^2 -2|a||b|cos\theta \\|a-b|^2 = (a_1-b_1)^2+(a_2-b_2)^2+(a_3-b_3)^2 \\ |a|^2 = a_1^2 + a_2^2+a_3^2 \\ |b|^2 = b_1^2 + b_2^2+b_3^2

(a_1-b_1)^2+(a_2-b_2)^2+(a_3-b_3)^2 = a_1^2 + a_2^2+a_3^2+b_1^2 + b_2^2+b_3^2-2|a||b|cos\theta

정리하면

-2a_1b_1-2a_2b_2-2a_3b_3=-2|a||b|cos\theta \\a_1b_1+a_2b_2+a_3b_3=|a||b|cos\theta

좌항은 a,b의 내적이므로

a\cdot b = |a||b|cos\theta

Data analysis, statistics