
1. Multiple Regression(다중 회귀)
1.1 R-squared(결정계수)
- 구하는 방법:
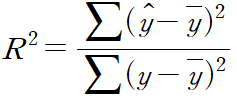
- 의미:
실제치(y)&평균(y bar)와 추정치(y hat)&평균(y bar)를 비교하는 것.
회귀선이 얼마나 잘 추정하는지를 보여준다.
0과 1사이의 값으로 나타나는데, 1에 가까울수록 성능이 좋다고 볼 수 있다.
1.2 Train/Test data
- 나누는 이유: 용도를 구분한다고 생각하면 된다. 먼저 Train data로 훈련을 시키고 Test data로 평가를 해보는 것.
즉, 훈련된 모델의 성능을 검증해보기 위해 사용한다.
예) 학생들이 시험을 치기 전에 기출문제, 문제집 등으로 학습(Train)을 하고, 기말고사로 평가(Test)해보는 것. - 유의사항:
시계열 자료 - 나눌 때에 시간의 흐름에 유의해야한다.
(예전 데이터로 새로운(가까운) 데이터를 test)
나머지 자료 - 랜덤 추출을 해본다.
무엇을 '예측'해볼 것인지 정의하는 것이 중요하다!
1.3 Multiple Linear Regression(다중 선형 회귀)
- Simple Linear Regression(단순 선형 회귀)과의 차이: 단순 선형 회귀는 독립변수(x) 하나, 종속변수(y) 하나. BUT 다중은 독립변수를 2개 이상 사용한다.
예) 대한민국 경제 성장률을 분석: 단순 - 대한민국 출산율 / 다중 - 출산율, 수출액, 환율 등등 고려 - 회귀계수 해석:
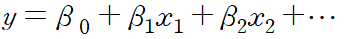
b0는 절편값. b1은 x1이 한 단위 변화할 때 y값에 미치는 정도. b2도 x2가 한 단위 변화할 때 y값에 미치는 정도.
예) b1 = 169.238 이면 x1이 한 단위 증가하거나 감소하면, y는 169.238만큼 증가하거나 감소한다. b2 = -27이면 x2가 한 단위 증가하거나 감소하면, y는 반대로 27만큼 감소하거나 증가한다.
1.3.1 Evaluation metrics(모델 평가 지표)
- MSE: 많이 사용한다. 단점: 제곱을 사용해서 단위 Scale의 영향을 많이 받는다. 공분산 때와 마찬가지로 오류를 확인할 때에 이 값이 어느정도의 오류인지 알기 어렵다. 제곱을 사용하기에 이상치의 영향에 민감하다.

- MAE: 단위 Scale이 고정되어 있다. 직관적으로 이해하기 쉽다.

- RMSE: MSE의 단점을 개선한 방법
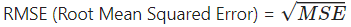
- R-squared: 결정계수라고도 부른다. 회귀모델의 설명력을 수치화해서 표현한다. 다중회귀분석에서 사용하기 위해 Adjusted R-squared를 사용하기도 한다.
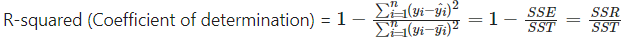
1.4 Overfitting(과대적합)과 Underfitting(과소적합)
-
Generalization(일반화): 일반화는 특정 사례들을 통해 일반적으로 통용될 수 있는 개념이나 공식으로 만드는 것을 의미한다. 여기에서는 Train 데이터를 사용해서, 기존 데이터가 아닌 새로운 데이터에서도 잘 작동하는 모델을 만드는 것을 의미한다.
-
Overfitting(과대적합):
뇌절이라 생각하면 쉬울까?모델이 Train 데이터만 너무 학습해서, 다른 데이터에 사용할 수 없는 것. 일반화에 실패했다. (아래의 그림에서 오른쪽 그래프라 생각하면 된다!)
머신러닝에서 과대적합은 피할 수 없고 완벽히 해소할 수도 없다. 다만, 이를 얼마나 적절히 조율해줄 수 있느냐가 중요해진다.
* 과적합을 해소하는 방법: 규제(정칙화/Regularization), Big data(데이터의 양을 늘려 큰 수의 법칙을 사용할 수 있다), Balanced data(데이터가 고루 분포된 데이터를 사용한다) -
Underfitting(과소적합): 훈련데이터에 적응도 못하고, 일반화에도 실패했다. 그래서 Train/Test 모두 실패.
1.5 Bias/Variance Trade-off
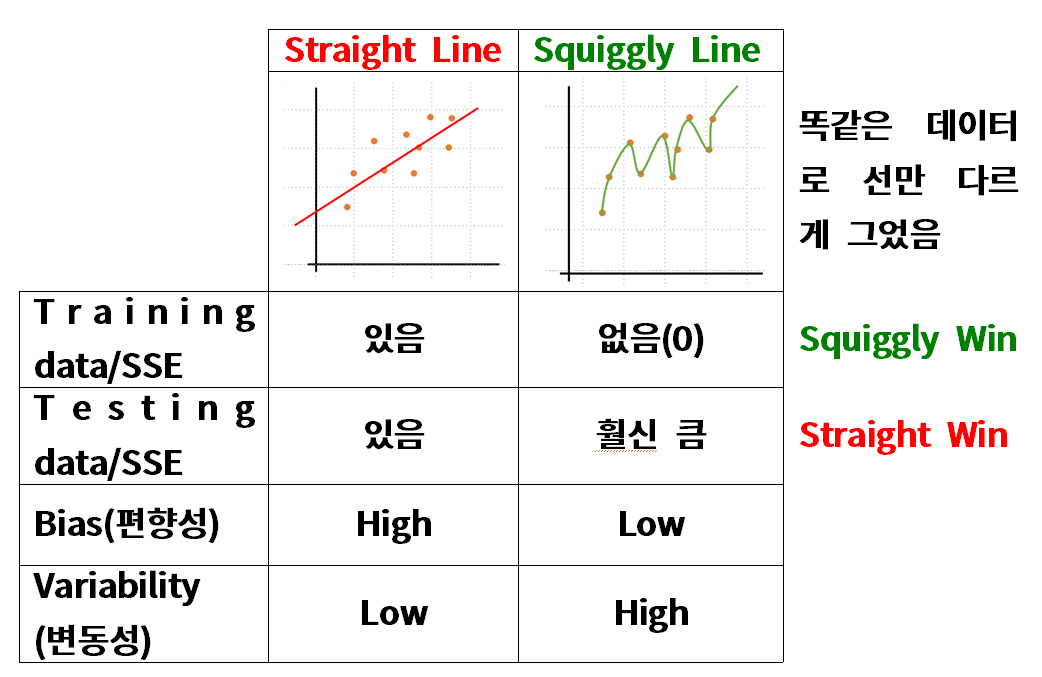
- 분산이 높은 경우(오른쪽)은 모델이 Train 데이터에 예민하게 반응해서 Test에서는 일반화를 잘 못하는 과대적합인 상황
- 편향이 높은 경우(왼쪽과 비슷한 상황)는 모델이 Train 데이터에서 Input과 Output을 잘 파악하지 못하는, 과소적합 상태다. (물론 지금의 데이터에서는 문제가 크게 없고, 저런 비슷한 상황으로 이해하면 좋겠다.)
- MSE는 결국 Bias, Variance, irre로 나뉘게 된다.(여기서 irre는 자체의 error로 못 없앤다.)
그래서 오류를 줄이기 위해서 Bias, Variance 를 줄여야 한다. - 하지만, 위 그림에서 볼 수 있듯이 편향을 낮추기 위해서는 분산이 높아져야하고, 분산을 낮추기 위해서는 편향이 높아져야한다. 즉, Trade-off(쉽게 생각하면 반비례)관계이다.
- 그럼 얼마나 낮춰주어야 할까? 저렇게 삐죽삐죽하게 그래프를 그리기 위해서는 수식이 복잡해진다. 1차함수는 직선, 2차함수는 포물선, 3차함수는 변곡점(이었나?? 올라갔다가 내려갔다가 다시 올라가는)이 있어서 갈수록 복잡해진다.
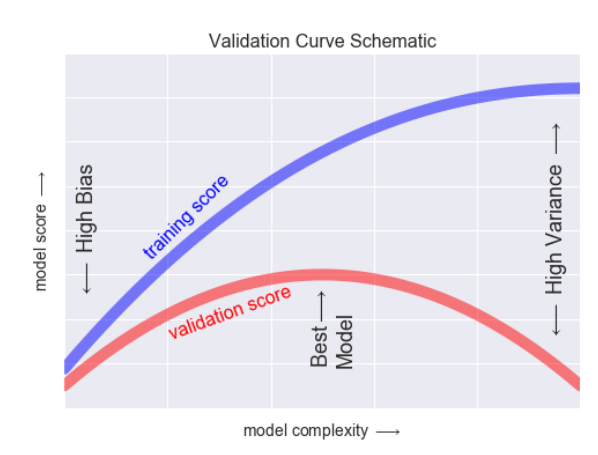
- (위의 그림을 누르면 자세한 정보를 알 수 있다.) 그래프에서 볼 수 있듯이 모델이 복잡하면 복잡할수록, Training Score는 끊임없이 상승하지만, Validation score(검사 점수, 여기서는 Test를 할 경우를 생각하면 되겠다.) 어느정도까지만 score가 올라가고 그 이후부터는 하락한다.
- 끊임없이 상승하는 것은 과대적합. 위의 그래프로 알 수 있는 것은 어느정도까지만 복잡하게 training을 하고 그 이후부터는 오히려 아무것도 하지 않는 편이 좋다는 것을 알 수 있다.
