[AIB]Note211 Simple Regression

1. Simple Regression(단순 회귀)

1.1 단순 선형 회귀선 그리기

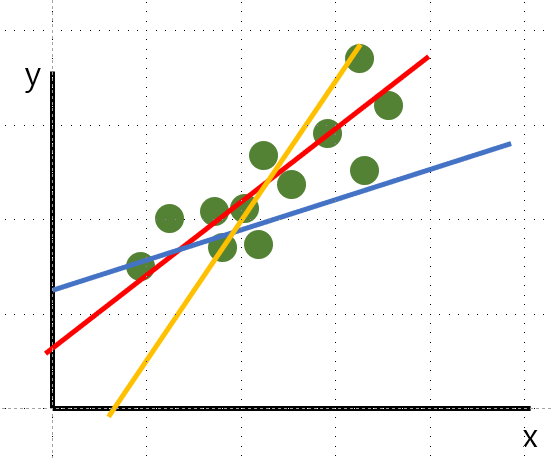
• 수집한 데이터가 위 그림처럼 표현되어 있다.
• 위 데이터를 선으로 잘 표현하고 여기에 없는 데이터를 잘 '예측'하기 위해서는 다른 색의 선 보다는 빨간색 선이 가장 좋을 것이다.
• 그럼 빨간색 선은 어떻게 구할 수 있을까?
  
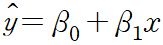
  y: 종속변수, 결과, 기대값, 추정값, dependent/estimated/expected value 등으로 표현할 수 있다.
  x: 독립변수, 원인, 실제값, actual/independent value 등으로 표현할 수 있다.
  beta0: y_intercept, y절편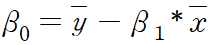
  beta1: slope, 기울기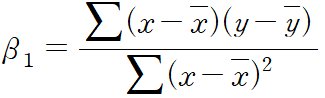
  로 계산할 수 있다.

1.2 Tabular Data

• 표 형태의 데이터를 의미한다.
• 각각의 Row(행)에는 Observation(관측치), Column(열)에는 Variable(변수)가 있으며, 데이터끼리의 관계를 알 수 있다.
• 각각의 열 내부에서는 데이터 타입이 모두 int, float, str 등 동일해야 한다.

1.3 주택 가격 예측하기

우리가 미래 주택가격을 예측을 한다고 하면 크게 두 가지 방법으로 예측을 할 수가 있을 것이다.

• 첫째: 과거의 경험을 바탕으로(예, 부동산 불패신화!!! 부동산은 망한 적이 없으니 빚을 내더라도 사야 해!!! 영끌영끌🤑)
• 둘째: 통계 정보를 활용한다(예, 주위 시세, 부동산 정책, 주위 수요/공급 현황 등)

여기서 우리는 당연히 통계 정보를 활용하는 방안을 살펴본다.

1.3.1 Linear Regression(선형 회귀)

일전에 지도학습과 비지도학습에 대해 살펴보았는데, 선형 회귀는 지도학습에 속한다. 지도학습은 '답'과 '문제'로 나눌 수 있다. 1.1에서 언급한 것에 추가해서 합쳐서 정리를 해보자면,,,

• 답/종속변수: 반응(Response)변수, 레이블(Label), 타겟(Target), 결과, 기대값, 추정값, dependent/estimated/expected value
• 문제/독립변수: 예측(Predictor)변수, 설명(Explanatory), 특성(Feature), 원인, 실제값, actual/independent value 등으로 표현할 수 있다.

1.3.2 Baseline Model(기준 모델)

예측 모델을 구체적으로 만들기 이전에, 간단하고 직관적이고 최소한의 성능을 나타내주는 '기준'이 되는 모델이 기준 모델이다.
각 문제별로 기준 모델은 보통 다음과 같이 사용한다.

• 회귀문제(Regression): 타겟의 평균값('mean' 함수 사용)
• 분류문제(Classification): 타겟의 최빈값('mode' 함수 사용)
• 시계열문제(Time series): 이전 타임스탬프의 값.

1.3.3 Predictive Model(예측 모델)

• 맨 위의 Scatter plot을 다시 살펴보면, 빨간 선이 초록색 데이터들을 가장 잘 설명해준다고 볼 수 있다. 그렇다면, '가장 잘 설명' 해준다는 것의 기준은 뭘까?
  지금 쉽게 보면은 노란색과 파란색 보다는 더 적합한 것 같은데 우리가 실무에서 마주하는 데이터 분석에서는 그런게 나와있을 리가 없다...(왜냐하면 우리가 만들어야 하기 때문에....)
• 여기서 잔차(Residual)와 오차(Error)의 개념이 나온다. 예측값(Expected value)은 모델이 추정, 예측하는 값. 관측값(Observed value)은 실제로 관찰된, 측정된 값이다.
  잔차와 오차 모두 '예측값과 관측값의 차이'를 의미한다. 다만, 잔차는 '표본'에서 오차는 '모집단'에서 사용하는 표현이다.
• RSS(Residual Sum of Squares/잔차제곱합)이 가장 작은 값이 데이터를 가장 잘 설명해준다. 즉, 위의 산점도에서 빨간색 선의 RSS가 가장 적다고 볼 수 있다. 다른 말로는 SSE(Sum of Square Error/오차제곱합)라고도 부른다. (나는 학교에서 SSE라고 배웠었음...)
• 또한, 이 RSS 혹은 SSE가 회귀모델의 비용함수(Cost Function)가 된다. 머신러닝에서는 비용함수를 최소화 하는 모델을 알아내는 과정을 '학습'이라 일컫는다.
• 이렇게 잔차제곱합을 최소화하는 방법을 최소제곱회귀 혹은 OLS(Ordinary Least Squares)라고 부른다. (이것도 계량 공부할 때 거의 다 OLS로 돌렸었음.. So powerful...)

1.3.4 내삽과 외삽

말이 너무 어렵다.

• 내삽(보간, Interpolation): 두 지점 사이의 값을 추정한다고 생각하면 된다.
  예) 데이터에서 x는 1~50까지 있는데 25만 없고, y도 1~50까지 있는데 25만 없다. 이때 회귀선을 그어주고 그 회귀선에 x=25를 넣어주면 y의 값을 알게 된다. 이렇게 추정해보는 방법이 내삽
• 외삽(보외, Extrapolation): 지금까지의 관찰한 결과를 바탕으로 그 바깥을 추정하는 방법.
  예) 데이터가 x, y 모두 50~100까지 있다. 이 때 x=25일 때의 값을 알고 싶으면 내삽과 동일하게 회귀선을 긋고 x=25를 넣어주면 y의 값을 알게 된다.

예전에 배웠을 때 내삽의 경우는 괜찮을지 모르지만 외삽의 경우에는 조심해야 한다고 들었던 것 같다. 왜냐하면 내삽은 아무래도 범위 내의 데이터를 추정하는 것이기 때문에 괜찮을지 모르지만 외삽은 일어나지 않은 일을 추정하는 것이기 때문이라고 이해하고 있다.
예를 들면 if 월드컵을 해서 만약에 적벽대전에서 조조가 낚이지 않았다면?? (내삽) 삼국지를 잘 아는 사람들은 하루종일 마라톤 토론을 할 수 있을것. 하지만, 2134년에 세계 3차대전이 생긴다면?? 예측하기 어렵다.... 이렇게 이야기를 하면 와닿을 수 있으려나 모르겠다..

1.3.5 상관계수와 절편값

• Coefficient(상관계수): 상관계수의 값이 2.14가 나왔다면 x가 한 단위 증가하거나 감소할 때, y는 2.14단위 증가하거나 감소한다는 것. 갯수는 독립변수의 갯수만큼 있다.('model.coef_' 함수 사용)
• intercept(절편값): y=ax+b에서 절편값이 247이 나왔다면 x가 0일때, y의 값이 247이라는 것. 쉽게 생각하면 회귀선이 시작하는 스타트라고 보면 될 것 같다. 독립 변수의 값이 0일 때 y의 값이니깐 1개만 있다.('model.intercept_' 함수 사용)

1.3.6 Scikit-learn

머신러닝 모델을 만드는데 가장 많이 사용하는 라이브러리.

• 특성(독립/원인) 데이터와 타겟(종속/결과) 데이터를 나누어 준다.
• 특성 행렬은 주로 X로 표현하고 2차원 행렬, dataframe, 중첩 리스트를 사용한다.
• 타겟 배열은 주로 y로 표현하고 보통 1차원 형태. series, array, list를 사용한다.
  프로세스

1. 내가 풀어야하는 문제에 적합한 모델을 선택하여 클래스를 찾아본 후 관련한 속성이나 하이퍼파라미터(모델링 할 때 사용자가 직접 세팅해주는 값)를 확인해본다.
2. 문제에 따라 조금씩 차이가 있겠지만, 특성 행렬, 타겟 배열과 같은 데이터를 준비한다.
3. fit() 메소드를 사용해서 모델을 학습한다. (무엇을; 주어진 데이터를, return; 회귀 계수)
4. predict() 메소드를 사용해서 새로운 데이터를 예측한다.