[AIB]Note221 Decision Trees

노코멘트·2022년 3월 2일

AIB 학습

목록 보기

11/15

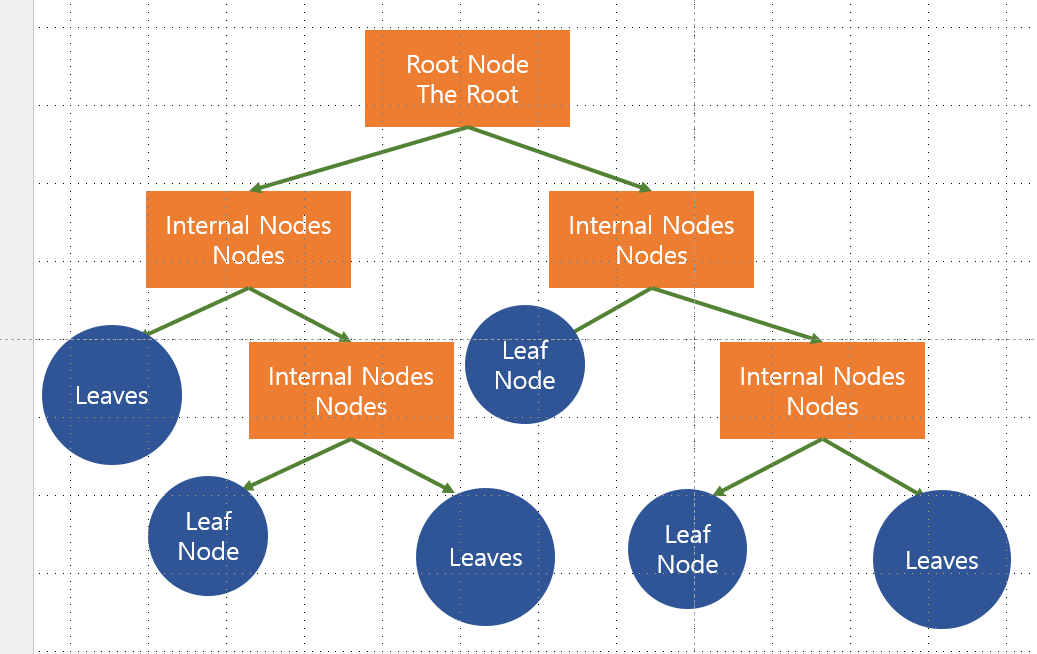
그림참조! root에서 시작해서 T/F를 통해 데이터를 구별한다.

회귀/분류 모두에서 가능하다!
선형회귀: 연속형 데이터 // 트리: 연속형, 범주형 둘 다 가능
특성이 많으면 선형회귀, 트리 둘 다 '과적합'과 '연산량 증가'의 문제가 생긴다.
비선형, 비단조(Non-Monotonic), 특성상호작용(Feature Interaction) 특징을 가지고 있는 데이터 분석에 적합하다.
Decision Tree(결정 트리)를 기본으로 앙상블(Ensemble), 랜덤포레스트(Random Forest), 그레디언트부스팅트리(Gradient Boosted Tree)를 공부한다.

각각의 질문에 대해 불순물(Impurity)을 측정하고 비교한다. 그 후 불순물이 작은 것을 선택한다.
즉, 여기서의 비용/손실 함수는 불순도. (선형회귀에서는 오차함수)
그럼 불순물은??

+ 데이터 형태에 따라서 나누는 법

Category: 각 카테고리에 맞게 불순도를 계산하여 낮은 거로 정한다.
Numeric: 1. Numeric 데이터를 낮은 순서에서 높은 순서로 정렬한다(=오름차순) 2. 인접한 값끼리 평균을 구해준다. 3. 각각의 값에 불순도를 구해준다.
Rank: Numeric과 비슷한데 모든 Rank에 대해서 불순도를 비교한다.
예) rank=4, rank <= 1, rank <= 2, rank <= 3까지만 해준다. rank <= 4는 모든 rank를 포함하고 있으므로 하면 안됨.
Multiple Choice: 예) 색이 Red, Green, Blue 인 경우 B/B or G/G/B or G/R/G or R로 한다. R or G or B는 rank와 마찬가지로 모든 항목을 포함하므로 하면 안됨.

장점: 특성을 해석하기에 좋다. 즉, 직관적인 모델이다. 그렇기에 실무를 수행할 때에 잘 모르는 타부서 동료들에게 설명이 가능하다. XAI(eXplainable Artificial Intelligence, 설명가능한 AI).
비선형 데이터에 활용할 수 있다.
스케일링할 필요가 없다.
단점: 과적합이 일어나기 쉽다. 이를 해결하기위해 다양한 방법이 있다.(min_samples_split, min_samples_leaf, max_depth를 통해 제한을 걸어주는 것!).
성능이 조금 떨어진다.
샘플에 민감해서 트리 구조가 잘 바뀐다.
스무고개 식의 노드를 거치면서 T/F를 하기 때문에 탐욕 알고리즘의 문제가 생길 수 있음.. 최적은 아니지만 그럭저럭 평타정도 치는 모델이 완성된다.
외삽이 안된다.

Pipeline을 통해 여러 Machine Learning 모델들을 같은 전처리 프로세스에 연결시킬 수 있다.(코드를 단순화 시켜, 반복 작업을 수월하게 할 수 있도록 해준다.)
Grid search를 통해 여러 하이퍼파라미터를 쉽게 확인하고 튜닝할 수 있게 해준다.
데이터 누수를 방지해서 혹시 모를 실수 등을 방지한다. (파이프라인을 사용하지 않고 직접 일일이 코딩을 해보니까 정말 내가 encoder, train, val, test, transform 등등 너무 헷갈리더라... ㅜ)

+ def 함수와의 차이.
def 함수도 마찬가지로 1번과 동일한 효과를 낸다. 즉, 여러 복잡한 코드를 함수 하나로 구현하여 실행시키게 할 수 있다는 것이다. 하지만 차이점은 2번과 3번에 있다. 특히 데이터의 누수를 방지한다는 점에서 큰 차이가 있다.