
1. Evaluation metrics for classification
1.1 Confusion Matrix(혼동행렬)
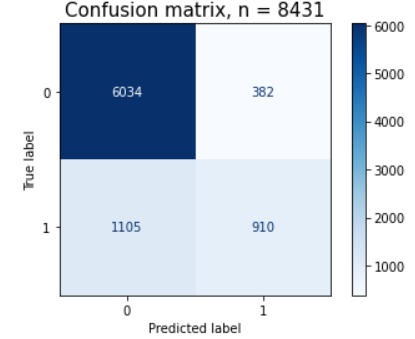
Confusion matrix는 혼동행렬이라 부른다... 왜냐하면... 해석하기가 너무 '혼동'이 오기 때문...? ㅋ
TP/TN/FP/FN으로 이루어진 매트릭스다. 분류 모델의 성능을 평가하는 여러 지표 중 하나.
- TP: True Positive - '찐양성' 실제 양성(1)인 상태를, 양성으로 올바르게 예측한 경우.
실제 코로나 확진자가 자가진단 키트(예측)를 사용했을 때 실제 '양성(1)'으로 나올 때. - TN: True Negative - '찐음성' 실제 음성(0)인 상태를, 음성으로 올바르게 예측한 경우.
코로나에 걸리지 않은 사람이 자가진단 키트를 사용했을 때 '음성(0)'으로 나올 때.(휴 다행....) - FP: False Positive - 능력부족
(능지부족)으로 (찐 음성인데) 양성으로 나오는 경우
코로나에 걸리지 않은 사람이 자가진단 키트를 사용했을 때 '양성(1)'으로 나올 때. (이럴때 PCR검사를 통해 보다 확실하게...!!) - FN: False Negative - 능력부족
(능지부족)으로 (찐 양성인데) 음성으로 나오는 경우
실제 코로나 확진자가 자가진단 키트를 사용했을 때, '음성(0)'으로 나오는 경우. (🚨비상비상🚨)
1.1.1 어떤 지표를 중요하게 봐야할까? → 그때 그때 달라요!
코로나 진단과 스팸 메일 분류를 할 때?
- 코로나를 진단할 때에는? 뭐가 더 혼란을 불러 일으킬까? 내가 양성(1)으로 판정받았는데, 기계의 오류 등으로 인해 판정이 잘못 나온 것이고 실제로는 음성(0)일때(FP). 혹은 내가 음성으로 판정받았는데, 실제로는 양성일 때?(FN) 후자일 것이다....
즉, 코로나 진단이나 암 등의 병의 진단에 있어서는 FN을 더 조심해야 할 것! - 스팸 메일을 분류 할 때에는? 코로나와 마찬가지로 생각해보면 쉽게 이해할 수 있다. 내가 받은 메일이 스팸 메일(1)이었는데, 메일함에 문제가 생겨서 일반 메일(0)로 될 때(FN). 아니면 내가 중요하게 받을 메일(0)이 있는데, 그게 스팸 메일(1)로 분류되서 스팸 메일함에서 나를 애타게 기다리고 있을 때..(FP) 전자와 후자 중 무엇이 더 치명적일까?? 스팸 메일이 일반 메일로 분류될 때에는 '아... ;;; 스팸메일 체크!' 하고 넘기면 될 터인데, 내가 요청한 자료나 파일이 스팸메일함에 있으면, '킹받는다..'
즉, 스팸 메일을 분류하는 문제에 있어서는 FP를 더 주의깊에 다루어야 할 것이다.
1.2 Accuracy, Precision, Recall
 참고자료
참고자료
1.2.1 Accuracy(정확도)
예측한 값이 실제 값과 얼마나 가까운지를 나타내는 기준.

얼핏 보면 어? 맞는거 아니야? 라고 생각할 수가 있다. 하지만 좀 더 자세히 살펴보면 얘기가 달라진다.
대한민국에 코로나 확진자가 10명(양성, 1)이 있다. 나머지는 5000만 명 모두 음성(0)이라고 했을 때, 어느 한 자가키트가 '무조건', '음성(0)' 이라고 한다면 어떨까?

위의 식을 살펴볼 때 정확도가 소수점 4자리까지 9로 찍힌다. 즉, 틀릴 확률은 극히 드물다는 뜻이다. 이런 코로나 검사 방법을 시행한다면, 조만간 전 국민이 슈퍼항체 보유자가 될 것이다;;;;
비유가 약간 이상하게 들릴 수도 있는데, 전하고자 하는 바는 이런 모델을 사용하면 안된다는 거다. 자가키트가 무조건, 음성을 말하는 상황을 바로 데이터 불균형이라고 한다. 키트가 무조건 0으로 찍어버리니, 정확도가 높더라도 우리는 신뢰할 수 없게 되는 것이다. 그렇기 때문에 홀/짝, 0/1 도박 하는 게임도 아니니,, 진짜 문제를 해결하기 위한 모델 설정이 필요하고, 진짜로 예측이 잘 되었는지를 확인할 필요가 있다!
1.2.2 Precision(정밀도)
분류를 진행했을 때에, 얼마나 많은 예측(분류 결과)치가 실제 값과 일치하는지.
모델이 1로 예측했을 때, 진짜로 1인 비율.
예측치를 기준으로 삼는다!
Of the Shoes classified Nike, How many are actually Nike?
Step1: Nike로 예측한 전체 합을 더한다. (Number of shoes classified as Nike) TP + FP(나이키로 예측한 수)
Step2: Nike로 예측한 경우 중에, 실제로 나이키인 경우를 구한다. (Number of shoes actually Nike, When classified as Nike) TP (찐 나이키)
Step3: Step2 / Step1 = TP / (TP + FP)
1.2.3 Recall(재현율)
실제 값 중에서, 얼마나 많은 예측(분류 결과)치가 실제처럼 분류 되었는지.
진짜 1인 값들 중에서 모델이 1로 맞춘 비율
실제값을 기준으로 삼는다!
Of the shoes that are actually Nike, How many are classfied as Nike?
Step1: 실제 Nike의 값을 모두 더한다. (Number of Shoes actually Nike) TP + FN(찐 나이키)
Step2: 실제로 Nike인데, Nike로 예측한 경우를 모두 합한다. (Number of shoes classified as Nike, When actually Nike) TP (찐 나이키)
Step3: Step2 / Step1 = TP / (TP + FN)
1.3 F-beta score
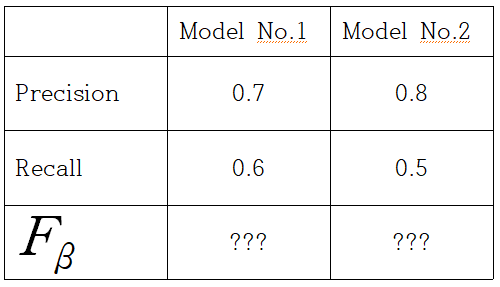
그럼 모델이 위의 표와 같이 두 개가 나와 있다. 어떤 모델을 써야할까???
???로 표시되어 있는 F-beta 값을 사용하면 된다.
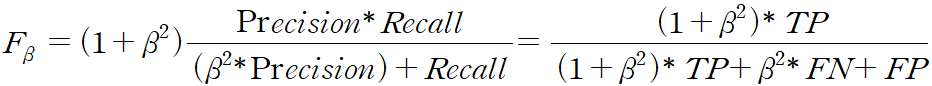
- F-beta that uses a positive real factor β, where β is chosen such that recall is considered β times as important as precision... 라고 위키피디아에 나와있다.
대충 beta는 precision이 중요한 만큼 recall이 beta 배로 여겨지도록 선택된다.고 해석 할 수 있겠다. 그리고 양의 실수(Positive real factor) - 즉, beta의 값이 높을수록 Recall의 영향을 더 많이 받는다. Recall의 중요도가 높아지게 되는 것!
- 비교는 F값이 높을 수록 성능이 좋다고 할 수 있다.
- beta가 1인 경우 Recall과 Precision의 조화 평균. 정밀도와 재현율의 가중치가 같게 된다.
1.4 ROC, AUC
위 두 가지 ROC, AUC를 사용하면 분류문제에서 임계값(Threshold) 설정에 대한 모델의 퍼포먼스를 구할 수 있게 된다.
1.4.1 ROC(Receiver Operating Characteristic)
임계값(Threshold)에 따른 재현율(Recall, TPR(True Positive Rate))과 위양성률(FPR, False Positive RatE)의 관계를 나타내준다.
재현율을 높이기 위해서는 Positive로 판단하는 최소 기준(임계값)을 계속 낮추어 모두 Positive로 판단하게 하면 된다. But 이렇게 하면 동시에 Negative 이지만, Positive로 판단하는 위양성률도 같이 높아지게 된다. 즉, Trade-Off 관계.
재현율은 최대로, 위양성률은 최소로 만들어주는 임계값을 찾아내는 것이 목적이다.
ROC가 왼쪽 위로, 밀접할 수록 좋은 모델 'ㄴ'을 밑으로 뒤집거나, 'ㄱ'을 왼쪽으로 돌렸을 때 나오는 모습처럼!!
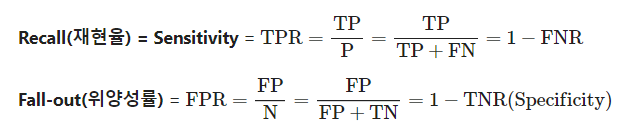
1.4.2 AUC(Area Under the Curve)
ROC curve 아래의 면적을 의미한다.
1.4.3 Threshold(임계값)
임계값은 default = 0.5. 즉, 0, 1 중에서 1로 나올 확률이 0.5이상이면 1로 판단하게 되는 것이다. 근데 이 값을 높이게 되면(엄격하게 적용) threshold = 0.8 / 0.9 등으로 하게 되면,, 좀 더 확실하게 1만 나오는 것들만 1로 판단하게 된다.
반면, 이 값을 낮추게 되면(느슨하게 적용) threshold = 0.4 / 0.2 등으로 하게 되면,, 좀 불확실하더라도 좀 더 0에 가까울 것 같더라도 1로 판단하게 된다.
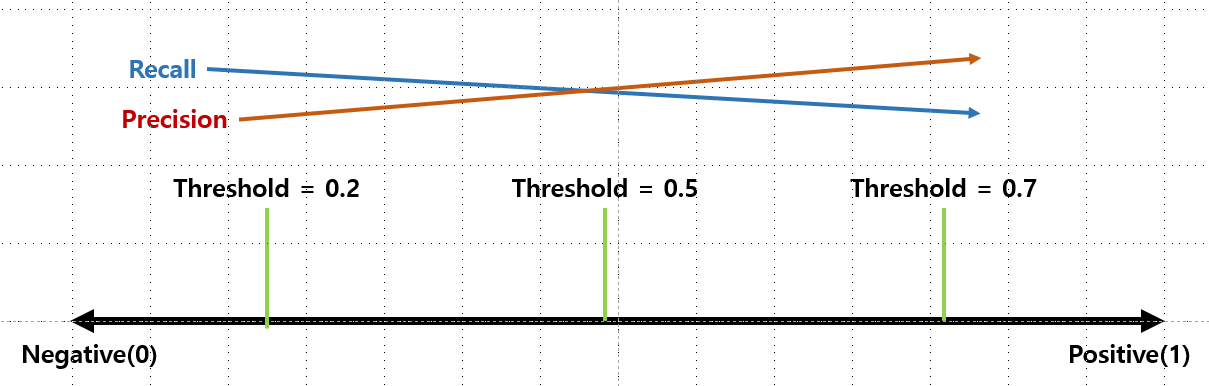
좀 더 직관적으로 이해할 수 있도록 만든 그래프.....
http://www.navan.name/roc/ 직접 확인해 볼 수 있는 사이트....
하지만, 하이퍼파라미터 등을 사용해서 직접 모델을 돌리는 것 같지는 않았다...
y_pred_optimal = y_pred_proba >= optimal_threshold
y_pred_07 = y_pred_proba >= 0.7이런 식으로 직접 지정해주거나 condition을 걸어주는 식으로 사용하는 것 같았다. 대신 라이브러리로 'Binarizer'가 있었다. 하지만 알려주신 분도 직접 사용해보지는 않았고, 이런 게 있다라는 정도로만 알고 있다고...
그래서 결론, 그냥 개념적으로만 알고 있거나 혹은 분류를 해야하는 코드를 작성할 때에는 위의 코드처럼 하드코딩(??맞나??) 식으로 해서 해주어야 할 것 같다.
+ F-beta score와의 차이점!
F-beta score는 모델의 성능을 평가하기 위한 지표! (for Train data set)
Threshold는 분류할 때에 사용하는 확률의 기준이 된다. (연구자가 직접 어느 정도로 엄격 or 느슨하게 분류할 것인지를 지정해주는 것)
