Chained Matrix Multiplication

Chained Matrix Multiplication

주어진 행렬들을 연쇄적으로 곱할 때, 곱셈의 횟수가 최소가 되는 행렬들의 곱셈 순서를 결정하는 알고리즘이다. 여기서 곱셈의 횟수는, 행렬 내부 요소 간의 곱셈 횟수를 말한다.

예를 들어, ij 행렬과 jk 행렬이 있을 때, 둘을 곱하면 기본적인 연산 횟수는 ijk번이다.

주의: 행렬의 순서를 바꿀 순 없다. 괄호로 우선순위를 정해주는 것.

그래서 이게 왜 필요한데?

행렬 하나가 함수 하나에 대응된다고 하면, 3차원 상에서 좌표 이동이나 위치 변화, 크기 변화 등에 행렬의 곱이 관여 한다. A, B, C, D라는 애니메이션 효과가 있다고 했을 때, X라는 좌표에 이 효과를 곱해 다양한 3D 영상 등을 만들 수 있다. 썸네일이 토이스토리 사진인 이유이다.

brute force 방식

행렬이 n개가 있을 때, 행렬의 곱셈 순서의 가짓수는 $t_n$ 이라고 하자.

이 중 한 가지 방법을 수행하면 행렬의 개수는 n-1이 될 것이고,

곱셈 순서의 가짓수는 $t_{n-1}$이 될 것이다.

A, B, C, D라는 4개의 행렬이 있다고 하면, 이것들을 곱하는 과정은 크게 3묶음으로 분류가 가능하다.

( i ) 방법의 모든 경우의 수는 B,C,D의 곱셈 순서를 정하는 경우의 수와 같다.

같은 논리로 ( ii )방법도 확인이 가능하다.

이를 관계식으로 나타내면 $T_4 = T_3 + T_3 + 1$으로 나타낼 수 있다.

이를 통해 점화식을 도출해 낼 수 있다.

$T_n >= 2 * T_(n-1)$

$T_2 = 1$

repeated substitution을 진행하면,

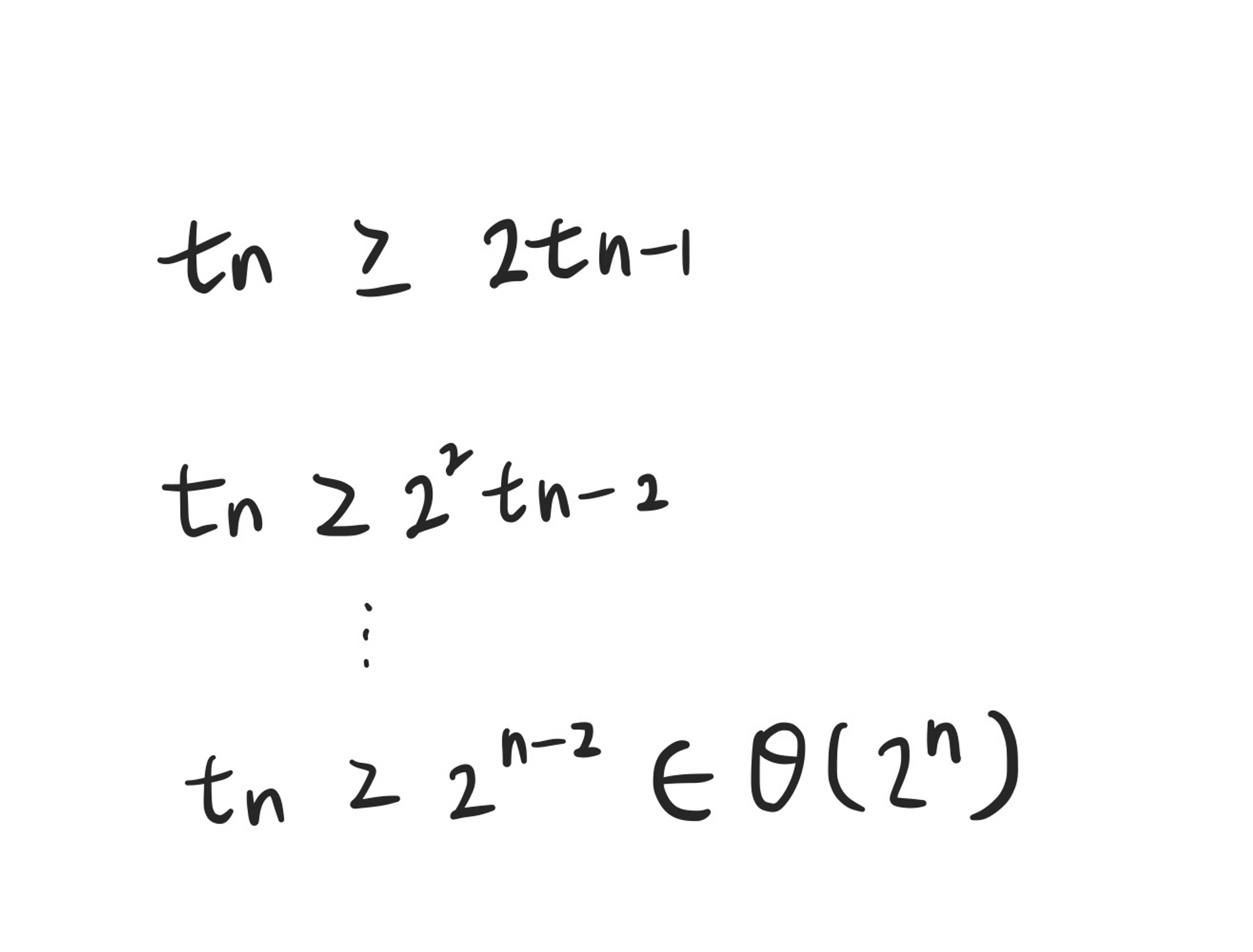
이므로 brute force방식으로 계산하게 되면 시간 복잡도가 exponential 하다.

따라서 이 방식은 사용하기에 비효율적이라는 것을 알 수 있다.

Dynamic Programming 방법

앞서 살펴본 brute force방식이 비효율적이므로 이번에는 dp를 이용해 문제를 해결하고자 한다.

알고리즘을 살펴보기 전에 알아야 하는 기본적인 용어와 기호에 대해 정리하도록 한다.

용어 정리

먼저 곱셈을 수행할 행렬이 $A_1, A_2, ... , A_n$ 으로 총 n개의 행렬이 있고,

그 행렬의 행의 수는 d배열에 $d_0, d_1, … d_n$으로 n+1개로 저장되어 있다.

코드를 짤 때는 d배열을 입력 받으면 된다.

교재의 설명은 다음과 같다.

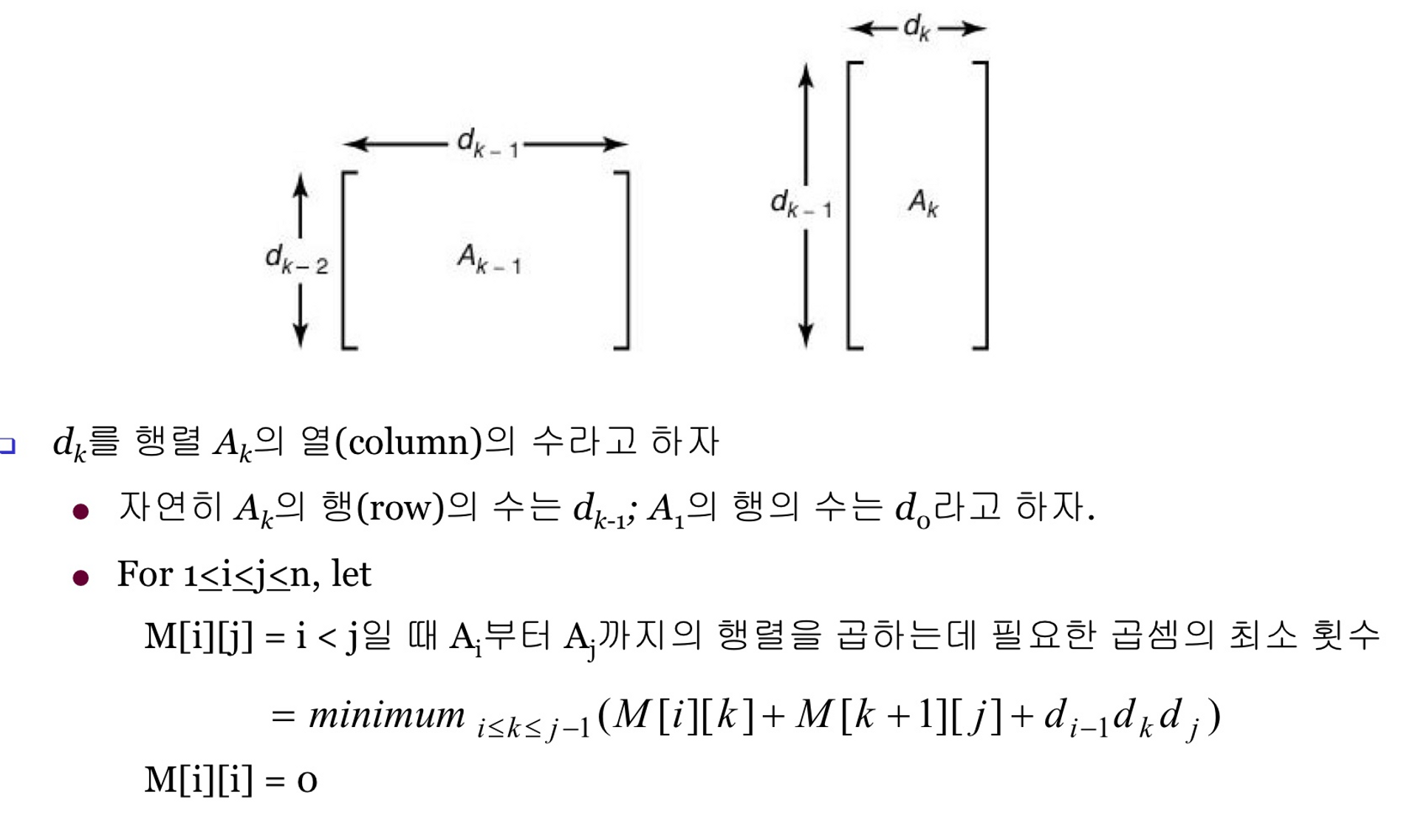
마지막으로 M배열에 의미에 대해 알아보자.

$M[1][6] = min(M[1][k] + M[k+1][6] + d_0*d_k*d_6)$ (1≤k≤5) 라는 식은

$A_1$ 에서 $A_6$까지 곱하는 최소 횟수를 구하는 식이다.

M[1][k]는 1~k번째 행렬을 곱해 한 행렬로 만들기 위해 곱하는 횟수이고,

M[k+1][6]은 k+1 ~ 6번째 행렬을 한 행렬로 만들기 위해 곱하는 횟수이다.

마지막 $d_0*d_k*d_6$은 앞서 만든 두 행렬을 곱하는 횟수이다.

k가 1부터 5까지 변하면서 그 중 최솟값을 구하는 과정을 수행한다.

예시로 이해하기

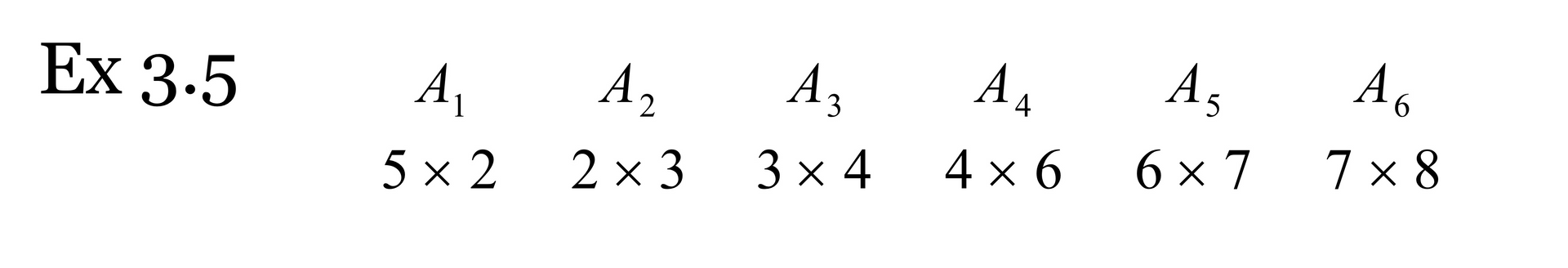
다음과 같은 예제가 있을 때,

M[4][6]은 4번째 행렬부터 6번째 행렬을 곱해 한 행렬로 만들기 위한 요소 간의 곱셈 횟수이다.

M[4][6] = minimum(M[4][4] + M[4][6] + 468, M[4][5] + M[6][6] + 478)을 계산해 답을 얻을 수 있다.

• 뒤에 곱하는(476) 숫자 헷갈리면 이거 보기

  

  

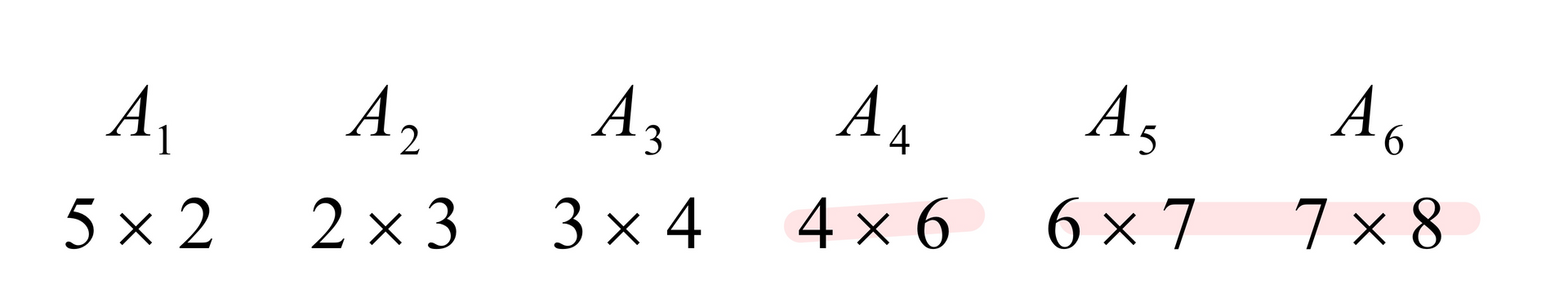
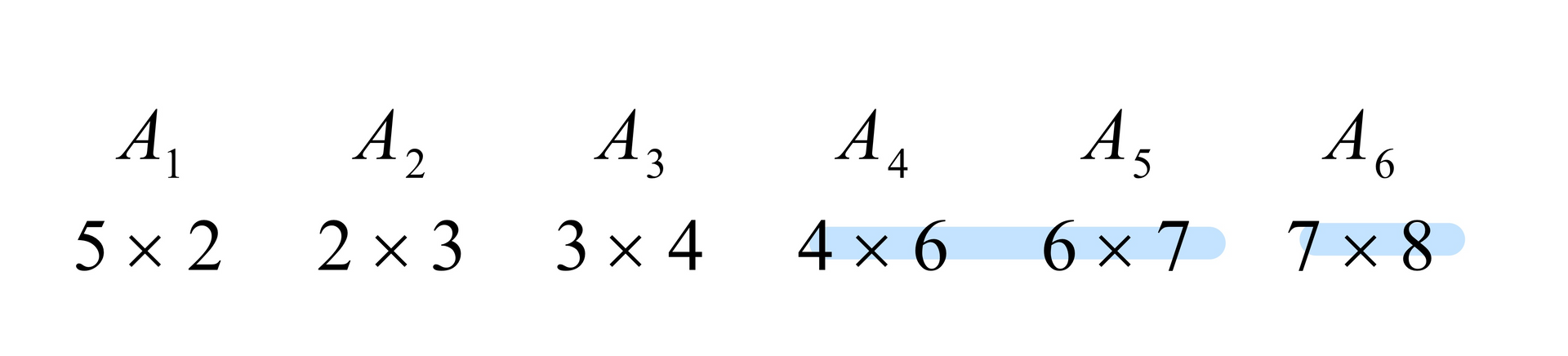
이를 배열에서 살펴보면

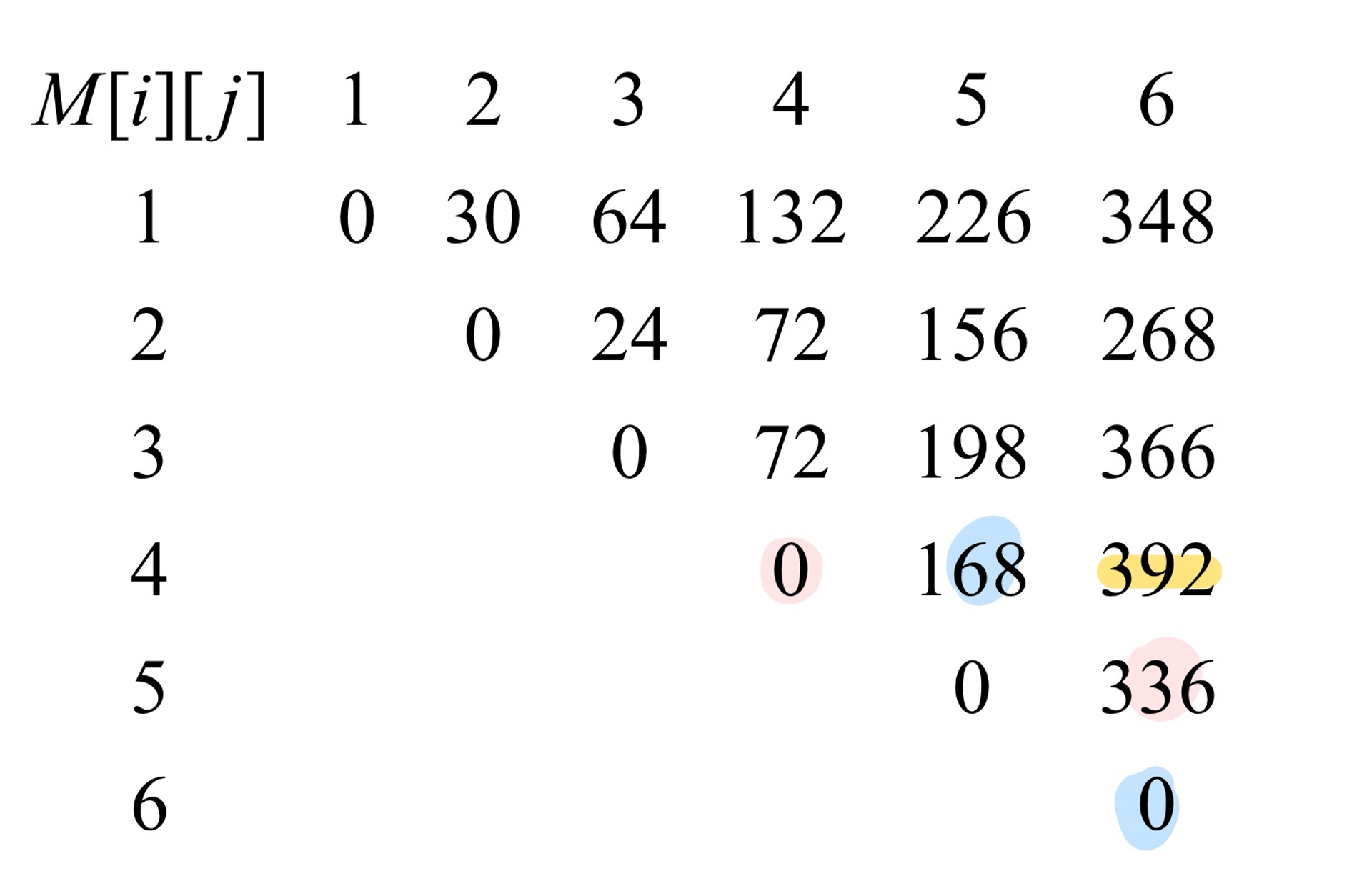
노란색에 위치한 숫자를 구하기 위해서는 같은 열과 같은 행에서 같은 색으로 칠한 숫자끼리 비교한다.

• P배열의 작동 원리

  !

  !

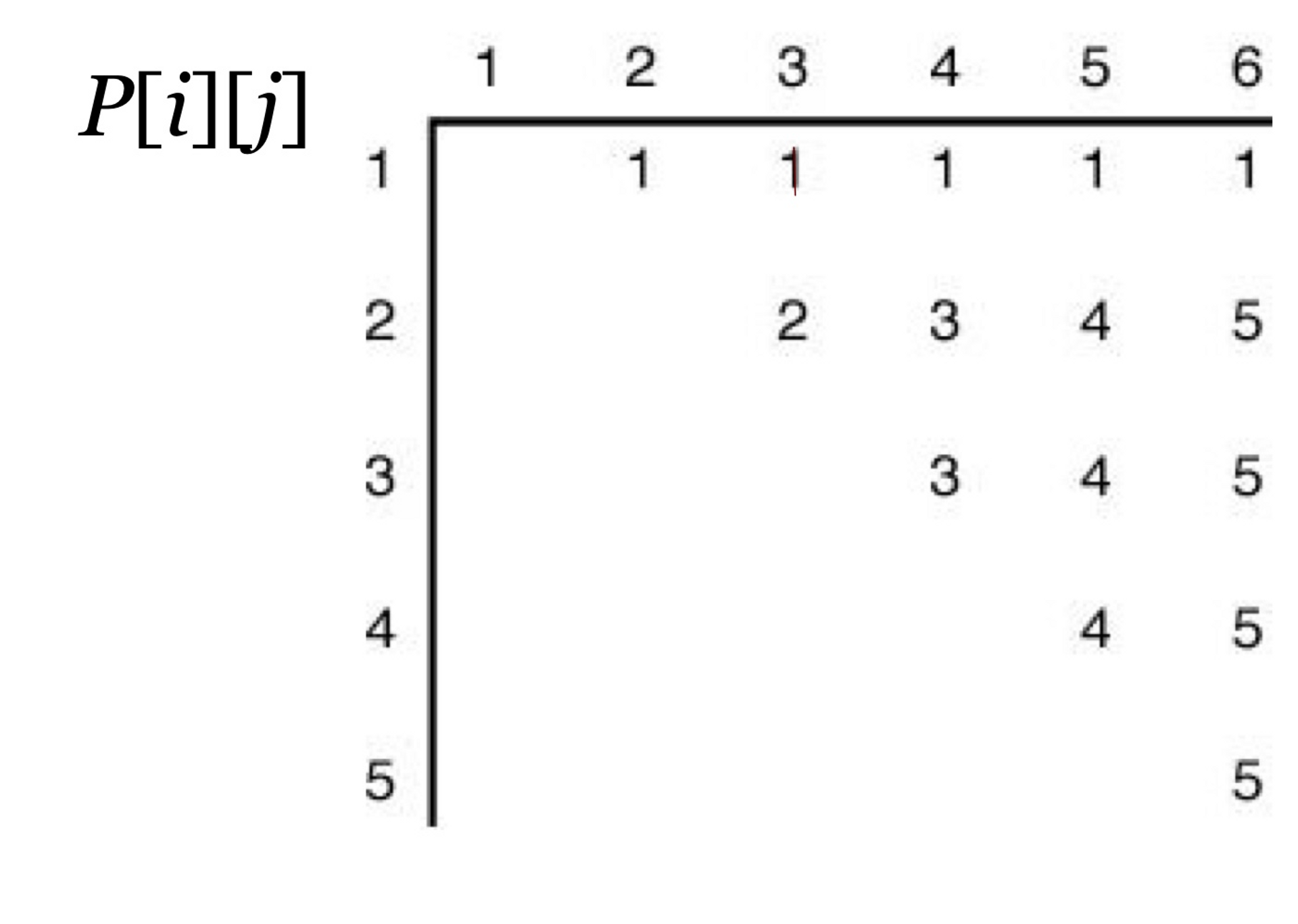
algorithm code

• 문제: n개의 행렬을 곱하는데 필요한 기본적인 곱셈의 횟수의 최소치를 결정하고, 그 최소치를 구하는 순서를 결정하라.
• 입력: 행렬의 수 n과 배열 d[0~n]
• 출력
  • 기본적인 곱셈의 횟수의 최소치를 나타내는 minmult
  • 최적의 순서를 얻을 수 있는 배열 P
  • P[i][j]는 행렬 i부터 j까지 최적의 순서로 갈라지는 기점을 뜻함

#include <algorithm>
#include <iostream>
using namespace std;

#define INT_MAX 987654321
int **P;

int minmult(int n, int *d, int **P) {
  int i, j, k, diagonal;

  int **M = new int *[n + 1];
  for (int i = 1; i <= n + 1; i++)
    M[i] = new int[n + 1];
  for (int i = 1; i <= n; i++)
    M[i][i] = 0;

  for (diagonal = 1; diagonal <= n - 1; diagonal++)
    for (i = 1; i <= n - diagonal; i++) {
      j = i + diagonal;
      int minimum = INT_MAX;
      for (int k = i; k <= j - 1; k++) {
        if (minimum > M[i][k] + M[k + 1][j] + (d[i - 1] * d[k] * d[j])) {
          minimum = M[i][k] + M[k + 1][j] + (d[i - 1] * d[k] * d[j]);
          P[i][j] = k;
          M[i][j] = minimum;
        }
      }
    }
  return M[1][n];
}

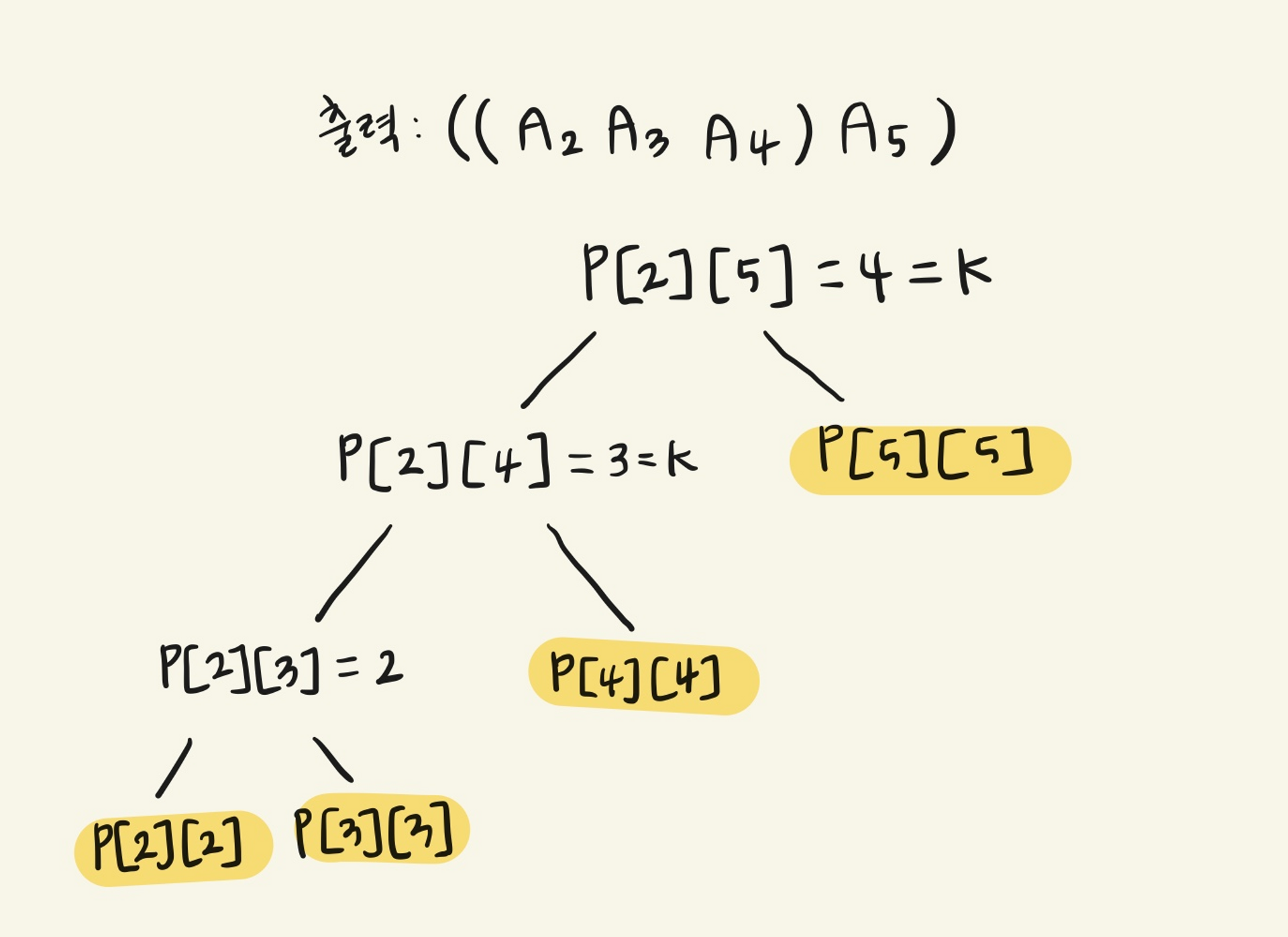
void order(int i, int j) {
  if (i == j)
    cout << "A" << i;
  else {
    int k = P[i][j];
    cout << "(";
    order(i, k);
    order(k + 1, j);
    cout << ")";
  }
}

int main() {
  int n;
  cout << "주어진 행렬의 개수를 입력하세요: ";
  cin >> n;

  int *d = new int[n + 1];
  cout << "행렬의 열과 행의 수를 차례로 입력하세요" << endl;

  for (int i = 1; i <= n + 1; i++) {
    cin >> d[i - 1];
  }
  P = (int **)malloc(sizeof(int *) * (n + 1));
  for (int i = 1; i <= n; i++)
    P[i] = (int *)malloc(sizeof(int) * n);

  int ans;
  ans = minmult(n, d, P);
  cout << "\n\nFinal answer: " << ans << endl;
  order(1, n);
}

분석하기 (every case)

• basic operation: 각 k의 값에 대하여 실행된 명령문, 최소 값인지를 알아보는 비교문
• 입력 크기: 곱할 행렬의 수 n