알고리즘

주어진 행렬들을 연쇄적으로 곱할 때, 곱셈의 횟수가 최소가 되는 행렬들의 곱셈 순서를 결정하는 알고리즘이다. 여기서 곱셈의 횟수는, 행렬 내부 요소 간의 곱셈 횟수를 말한다. 예를 들어, ij 행렬과 jk 행렬이 있을 때, 둘을 곱하면 기본적인 연산 횟수는 ijk번

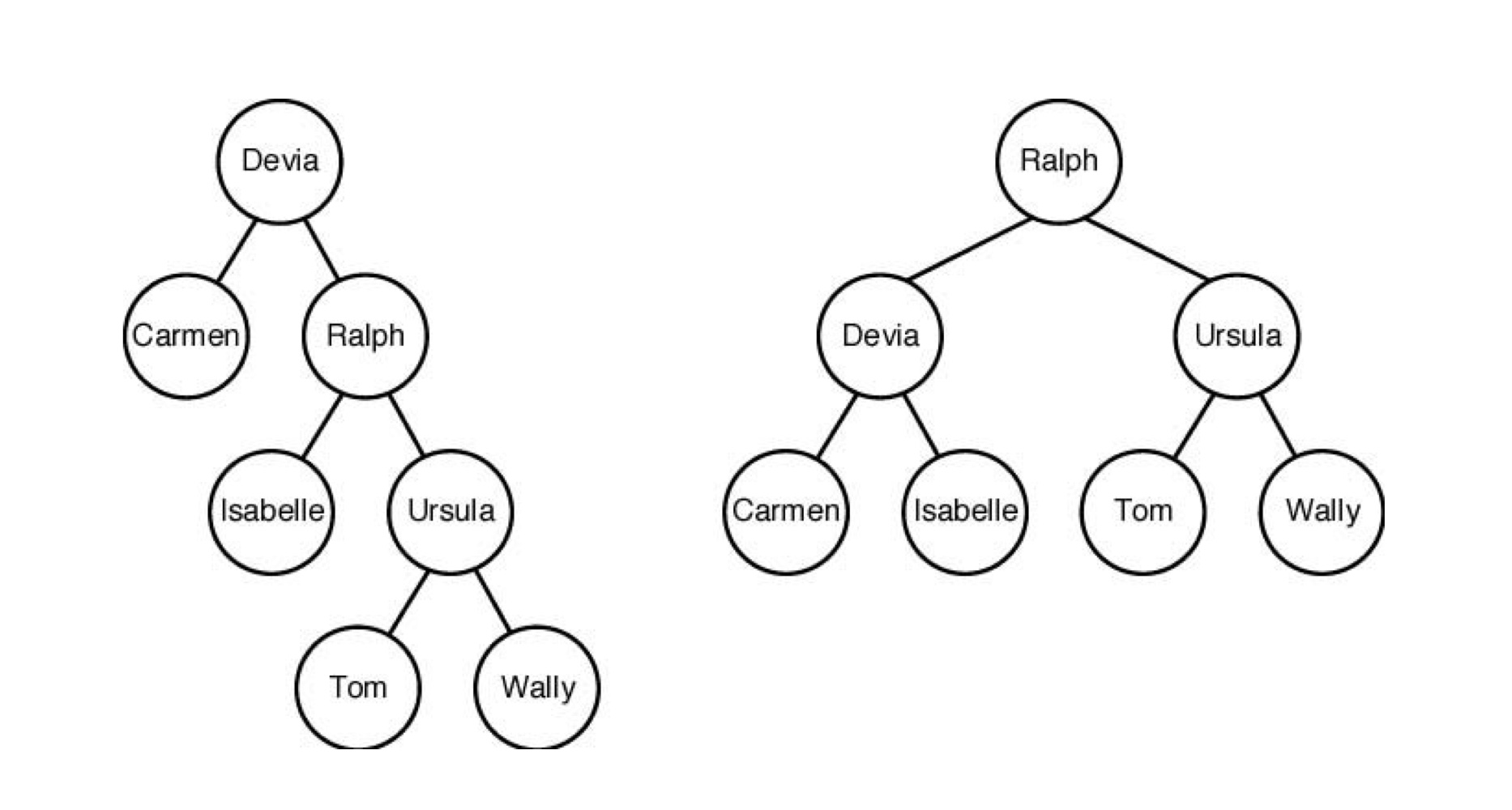
이진 탐색 트리의 KEY 값은 정렬된 배열이나 집합으로부터 만들어진다. 각 노드들은 한 개의 KEY값을 가진다. 한 노드의 왼쪽 자식 노드에는 자신보다 작은 값이 들어있고, 오른쪽 자식 노드에는 자신보다 큰 값이 들어있다.Depth: 루트 노드에서 자신까지 edge

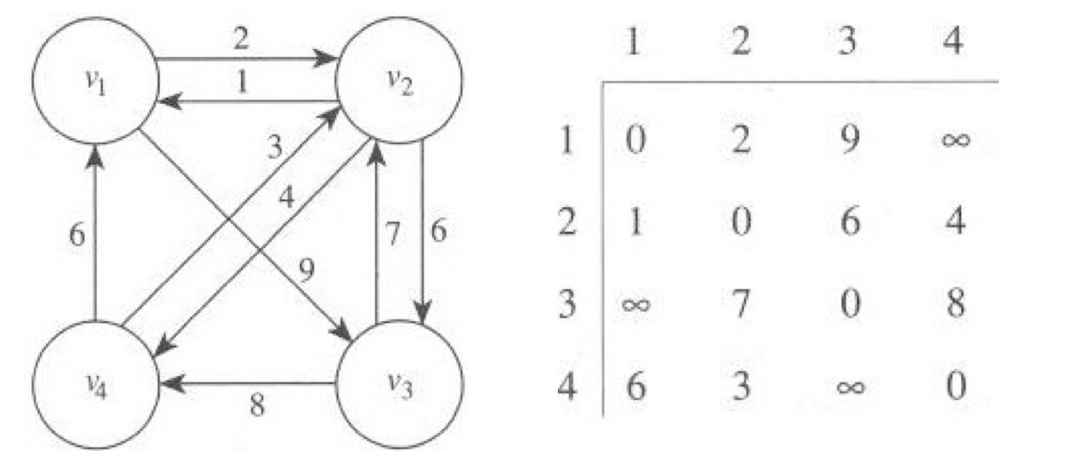
영업 사원이 고향에서 시작해서 각 도시를 한번씩 거쳐 다시 자신의 고향으로 돌아오는데 걸리는 최단 경로를 결정하는 알고리즘이다. 출발지를 빼고 각 노드를 한번씩 방문하는 경우의 수 이므로 Factorial의 가짓수가 나온다.$$(n-1)(n-2) ... 2 1 = (

최적화 문제긴 하나, 재귀적이지 않다.selection procedure(선정 과정)Feasibility checkSolution check눈에 보이는 것 중 가장 좋을 것 같은 답의 후보를 하나 고른다. 고른 하나가 답에 포함되는지, 조건을 설정하여 체크한다.새로 얻

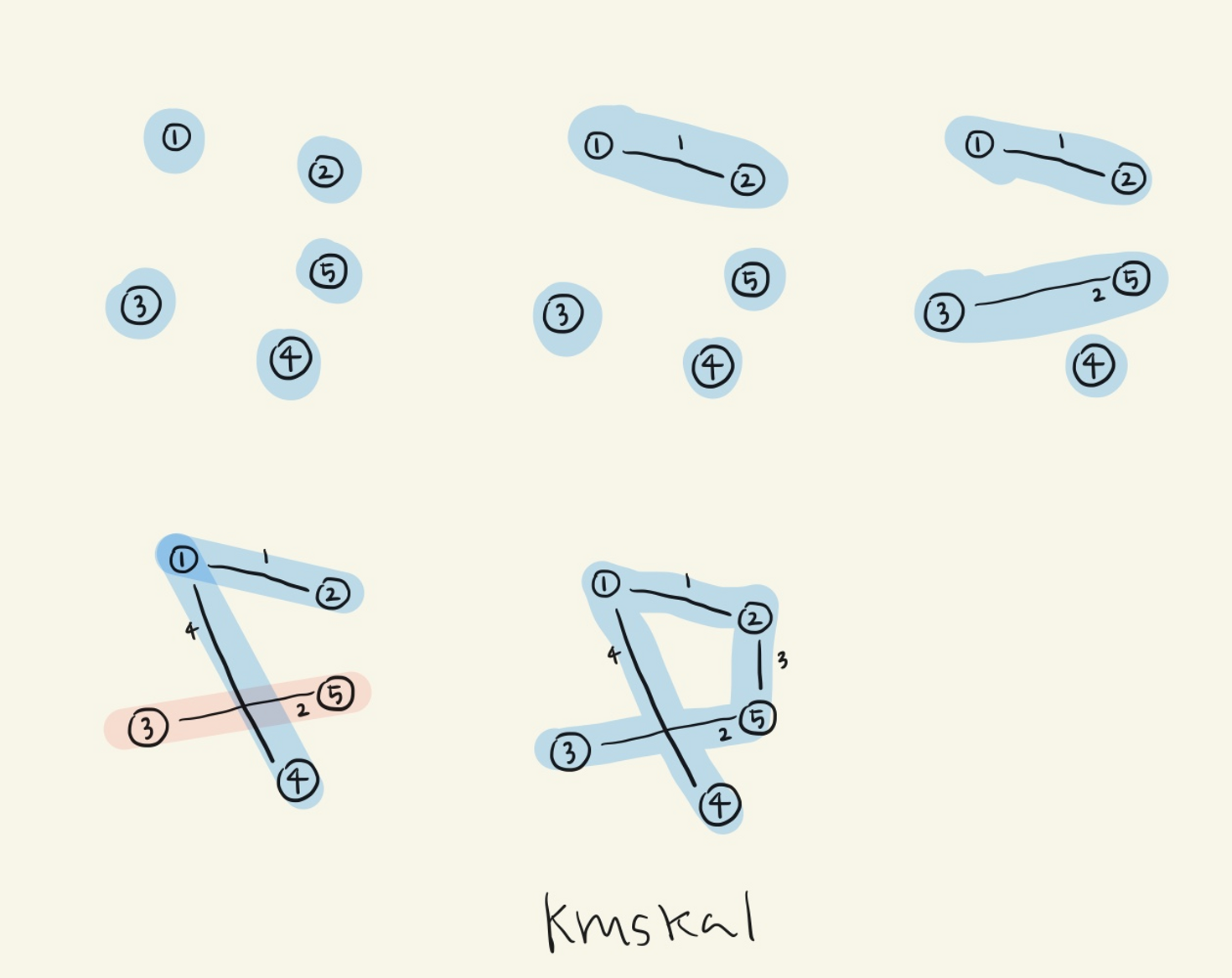
서로소란 두 집합간 공통된 부분이 없는 집합index i; set_pointer p, q;initial(n): n개의 서로소 부분 집합을 초기화 함p = find(i): i가 포함된 집합의 포인터를 넘겨준다.merge(p,q): 두개의 집합을 가리키는 p와 q를 합병한

가중치가 있는 방향성 그래프에서 한 특정 정점에서 다른 모든 정점으로 가는 최단 경로를 구하는 문제이다.아니다. 플로이드는 모든 노드가 출발지가 될 수 있지만, 다익스트라는 v1만 출발점으로 둘 수 있다. prim이랑 똑같다!prim알고리즘처럼 반복문이 총 N-1회 수

S = {item, item, … }w = weight of itemp = value of itemW = maximum weight of items in the knapsack$$\\sum \_{item_i \\in A}w_i$$위의 식을 만족하면서 $$\\sum \_

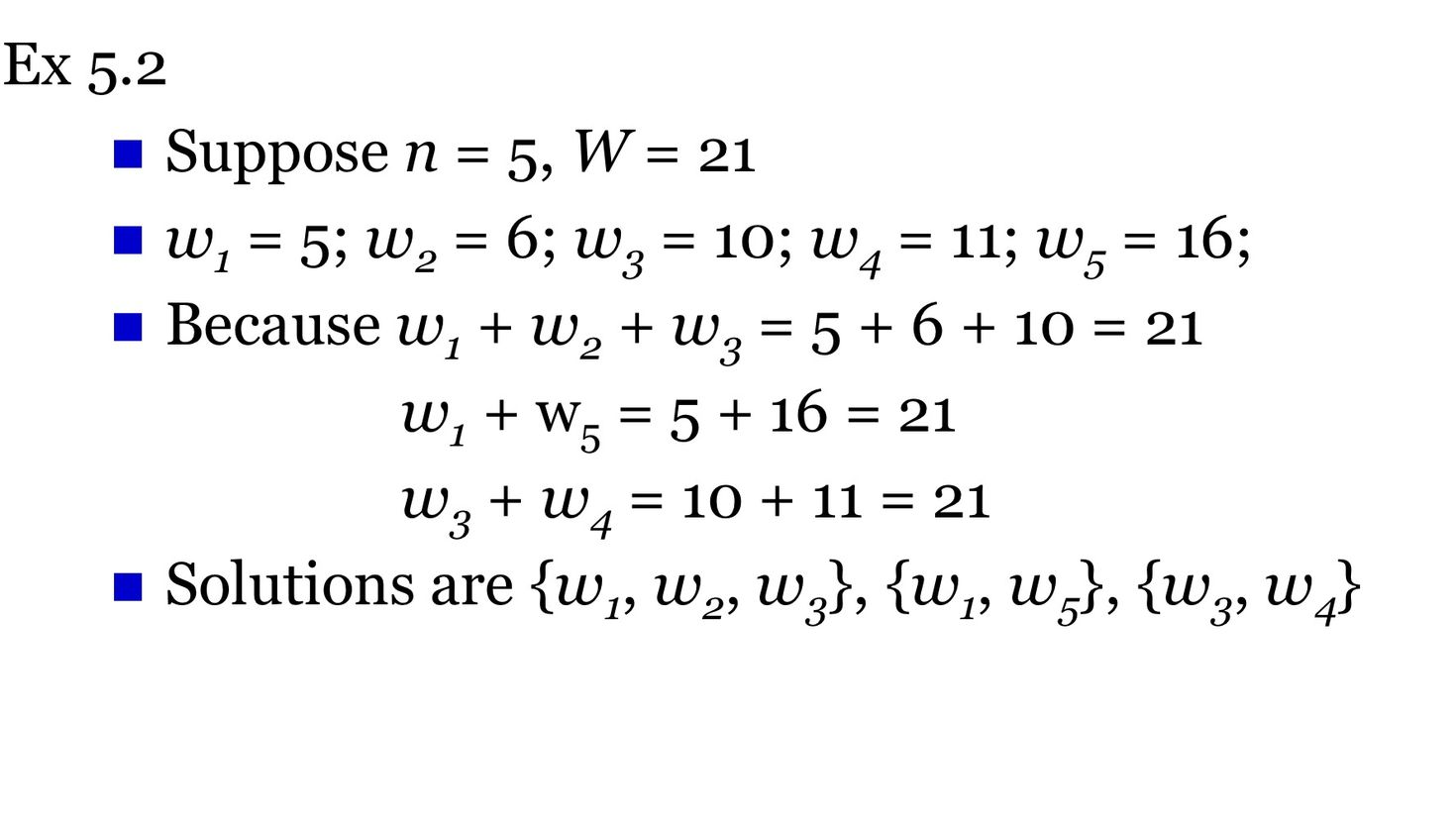
양의 정수인 w와 양의 정수인 W가 주어진다.⇒ 각 노드의 가중치인 w와 우리가 구해야하는 노드들의 합인 W가 주어진다.이 알고리즘의 목표는 노드의 가중치의 합이 W가 되는 모든 subset을 찾는 것이다.n의 개수에 따라 depth가 정해짐weight of node

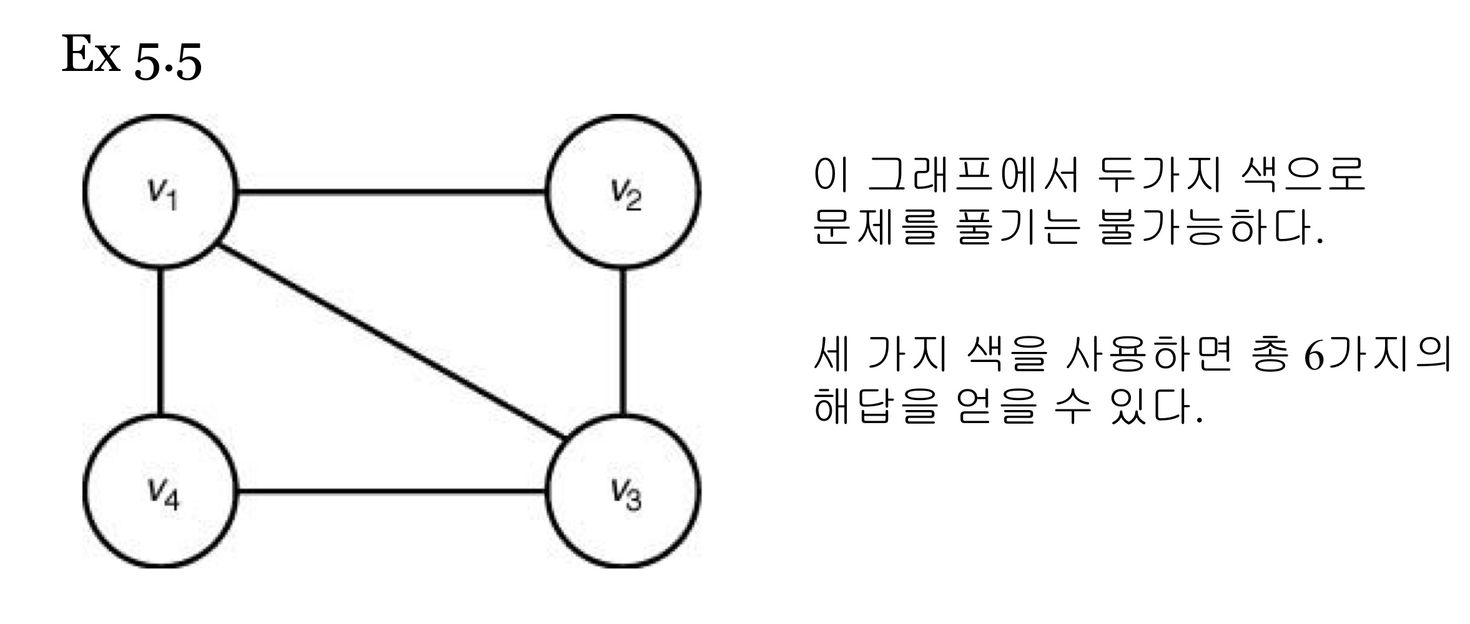
m-coloring: m개의 색을 가지고 인접한 지역이 같은 색이 되지 않도록 지도에 색칠하는 문제 지도에서 각 지역을 그래프의 정점으로 하고, 한 지역이 어떤 다른 지역과 인접해 있으며, 그 지역들을 나타내는 정점들 사이에 이음선을 그으면, 모든 지도는 그에 상응하

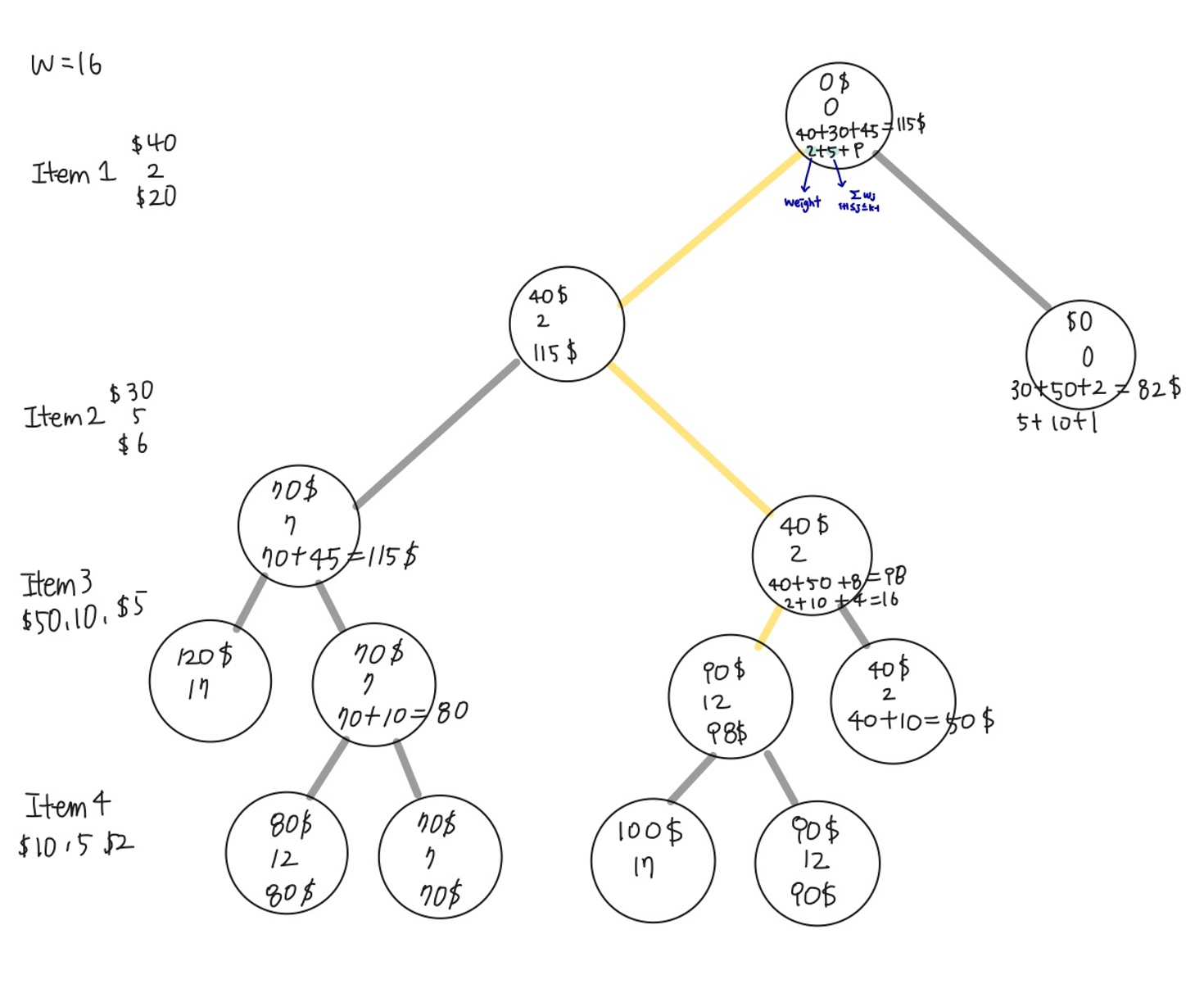
만들고자 하는 모든 경우의 수가 상태 공간 트리에 펼쳐져야 한다.⇒ sum of subset처럼 선택한 경우, 선택하지 않은 경우가 트리에 모두 그려져야 함.왼쪽으로 가면 배낭에 물건을 넣은 경우, 오른쪽으로 가면 배낭에 물건을 넣지 않은 경우속성이 두개이기 때문에 두

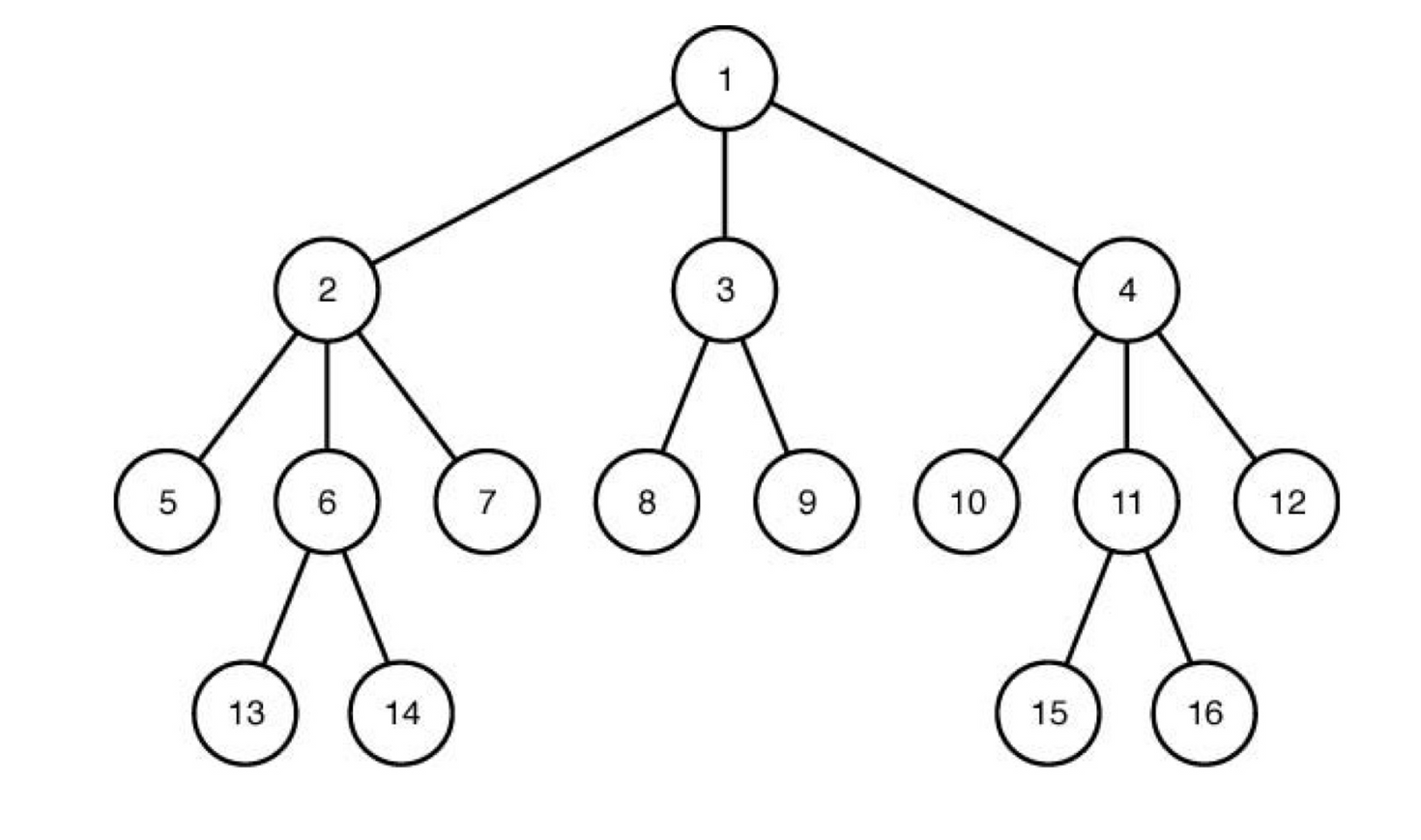
BFS를 사용하면 다음과 같은 순서로 노드를 방문한다.Depth First는 재귀적인 방식으로 노드를 방문하지만, breadth First는 Queue(이하 Q)를 사용한다.Q를 초기화 하고 루트를 방문해 할 일을 한다.root 노드를 먼저 Q에 넣어준다.반복문을 수행

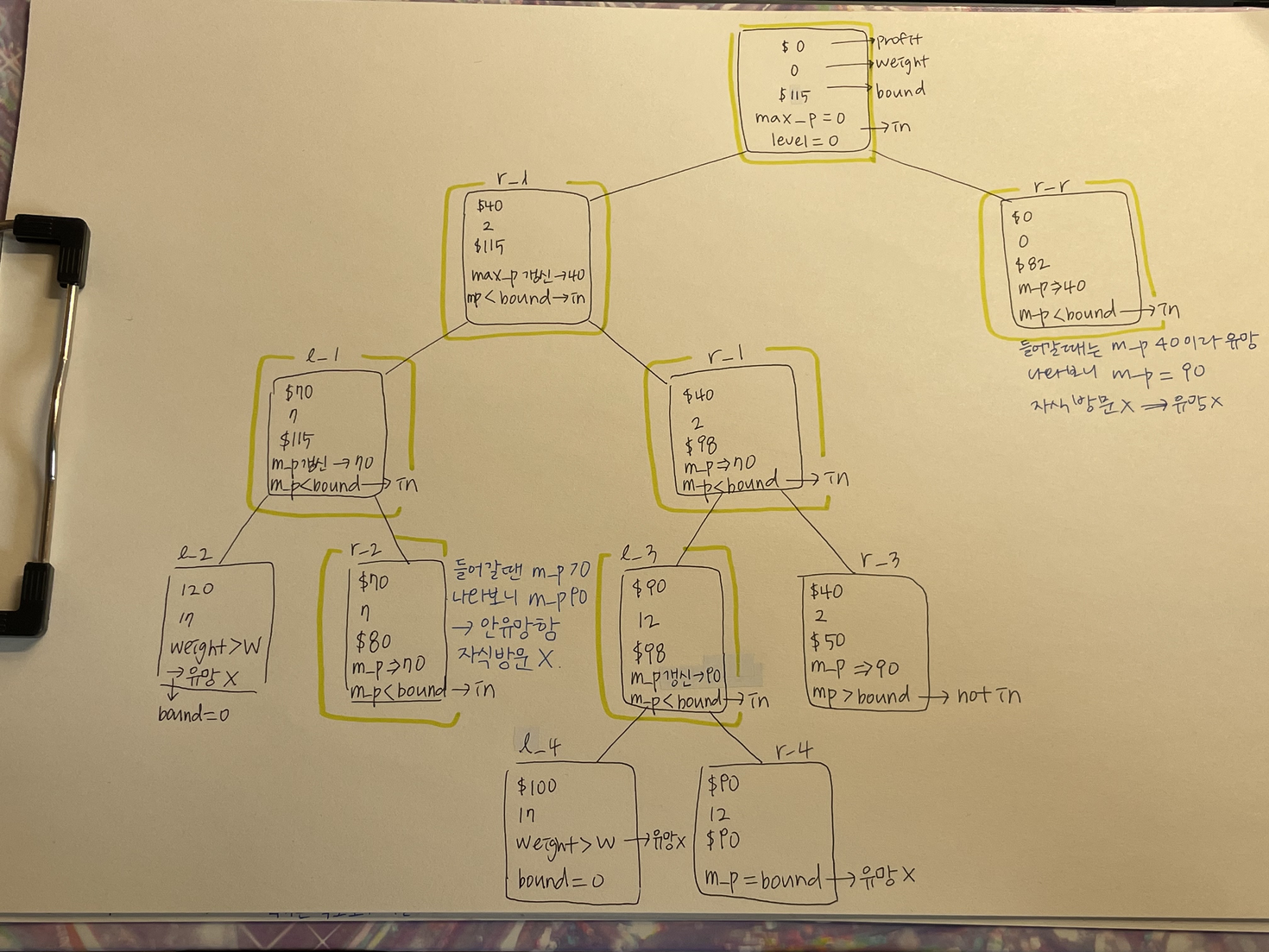
넓이 우선 탐색처럼 같은 level의 노드를 모두 탐색하는데, queue에 있는 노드 중 bound가 큰 애를 먼저 뺀다.⇒bound가 높은 것이 max_profit을 더 많이, 빨리 갱신할 것이라고 생각하는 것가능성 있는 애들만 선택한다고 볼 수 있음우선순위 큐를 사