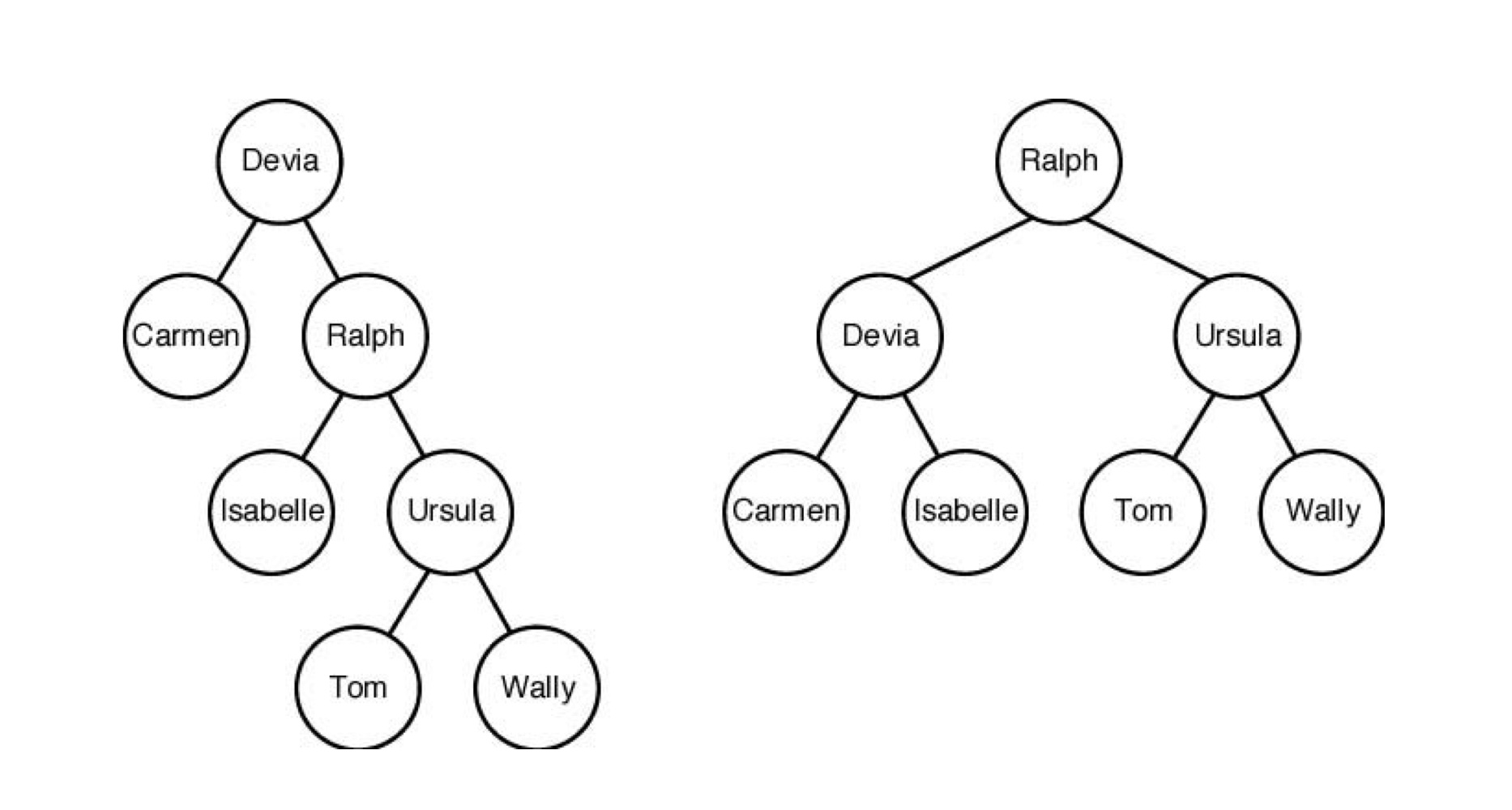
Optimal Binary Search Trees

int j =0;·2023년 2월 24일

알고리즘

목록 보기

2/12

Optimal binary Search Trees

Binary Search Tree

이진 탐색 트리의 KEY 값은 정렬된 배열이나 집합으로부터 만들어진다. 각 노드들은 한 개의 KEY값을 가진다. 한 노드의 왼쪽 자식 노드에는 자신보다 작은 값이 들어있고, 오른쪽 자식 노드에는 자신보다 큰 값이 들어있다.

Depth: 루트 노드에서 자신까지 edge의 개수를 의미한다. (노드의 level)
balanced: 만약 두 노드의 depth차이가 1이하면 그 두 노드는 balanced 하다고 한다.
optimal: 키가 위치하는 시간이 가장 작은 것을 optimal하다고 한다.

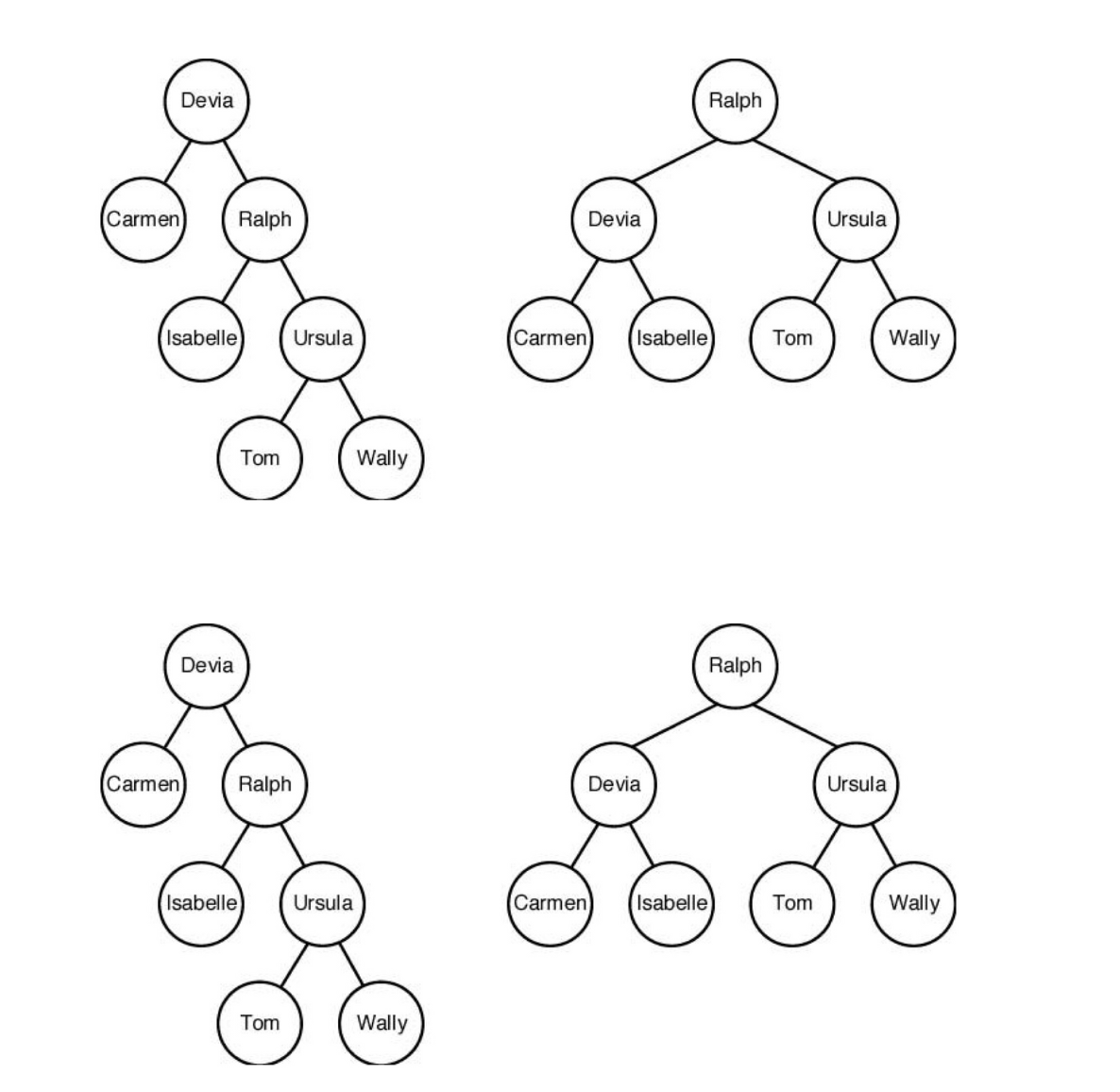
data types

struct nodetype{
			keytype key
			nodetype * left
			nodetype *right
}
typedef nodetype* node_pointer;

Optimal Binary Search Trees

이게 뭘 하는 알고리즘인데?

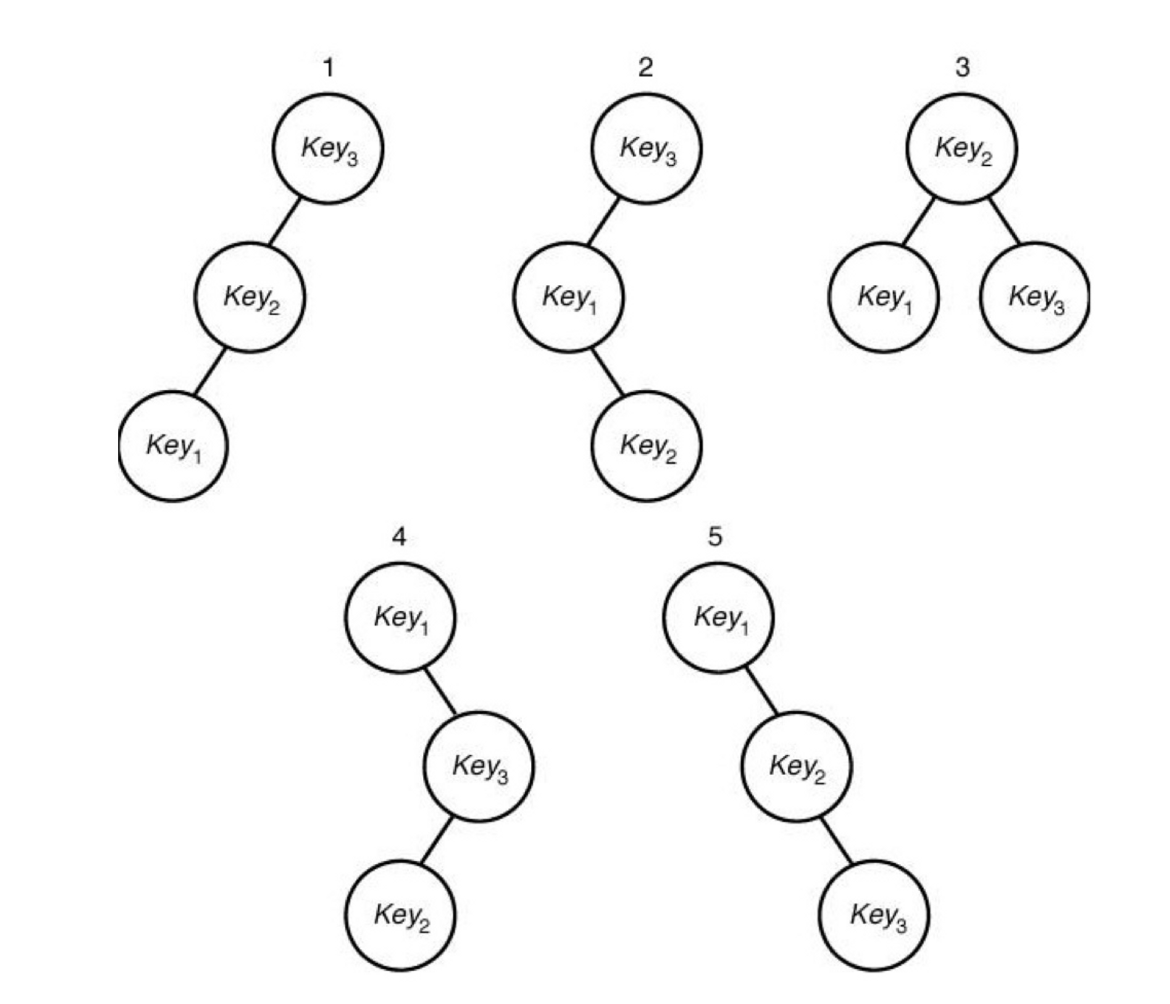
위의 그림과 같이 같은 key값이라도 여러 형태의 binary search tree를 만들 수 있다.

이 중에서 각 key값을 찾을 확률을 가중치로 두어,

이 가중치가 가장 적게 나오는 최적의 트리를 찾는 것이 이 알고리즘의 핵심이다.

key1을 찾을 확률: 0.7 , key2를 찾을 확률: 0.2, key3을 찾을 확률: 0.1이라고 하면 각각의 트리 중 최적의 값은 ‘확률* 그 key를 찾기 위해 탐색해야하는 횟수’ 를 통해 찾을 수 있다

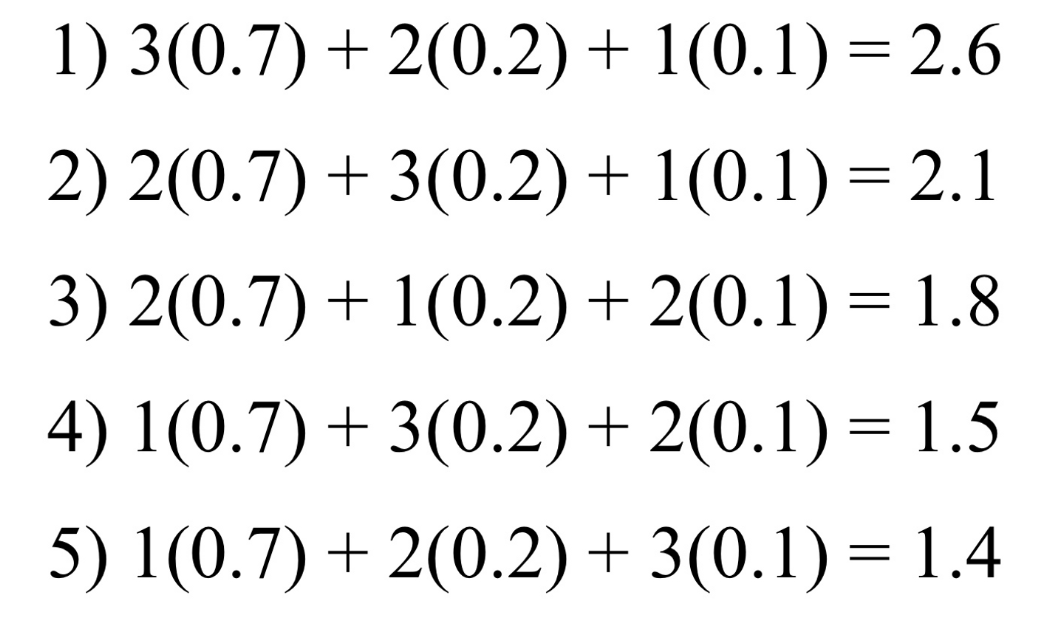
값이 가장 작은 5번째 트리가 제일 optimal하다고 말 할 수 있다.

점화식 이해하기

A[i][j] = minimum(A[i][k-1] + A[k+1][j]) + \sum_{\mathclap{i\le m\le j}} P_{m}

A[i][i] = p_i

A[i][i-1] = A[j+1][j] = 0

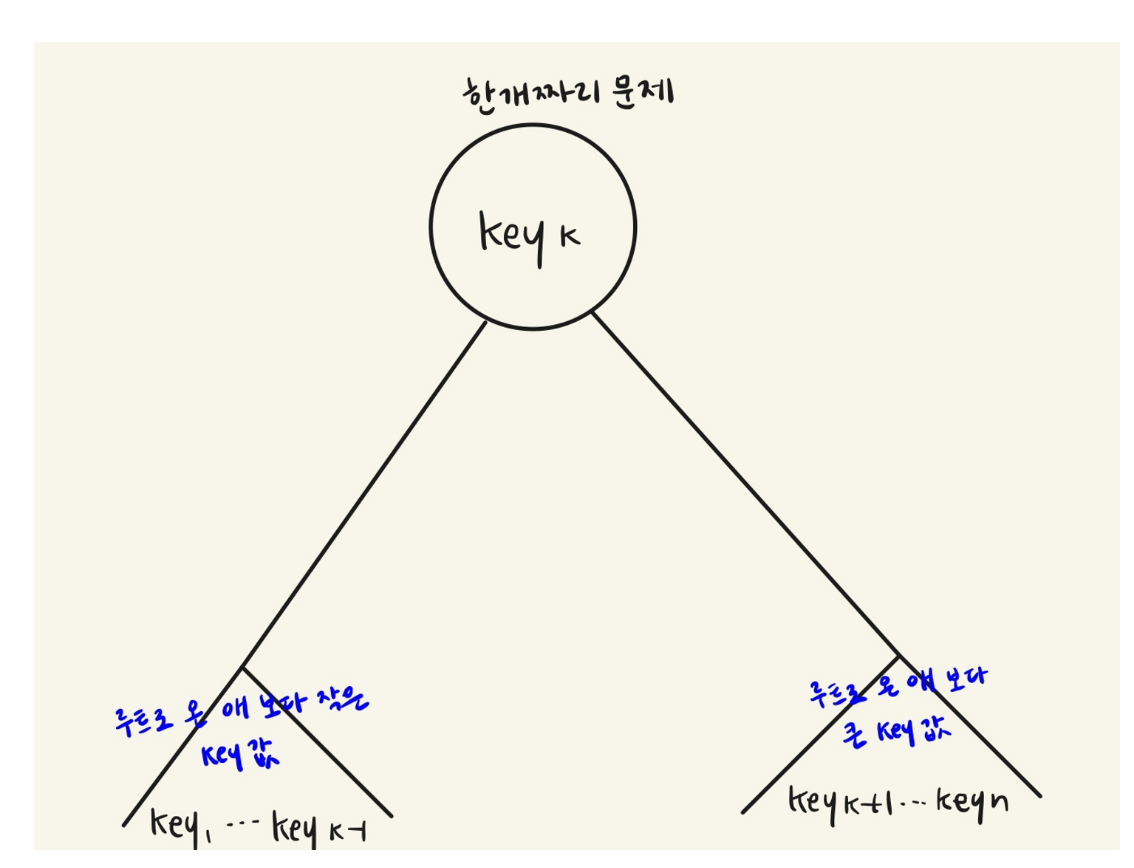
점화식으로 나타낸 트리의 구조를 그림으로 나타내면 다음과 같다.(이 경우는 i = 1, j = n인 경우⇒ 최종 답(?) 같은거임)

우리가 정한 k는 i부터 j까지의 sub tree에서의 루트 값으로, i $\le$ k $\le$ j 의 값을 갖는다.

이때 binary search tree의 성질에 따라서 i부터 k-1까지의 sub tree의 key 값은 k보다 작을 것이고

k+1부터 j까지의 sub tree의 key 값은 k보다 클 것이다.

왼쪽 sub tree의 탐색 시간은 A[i][k-1] 일 것이고, 오른쪽 sub tree의 탐색 시간은 A[k+1][j]일 것이다.

그래서 두 개를 더했을 때 가장 최소가 되는 k의 값을 정하는 것이다.

하지만, 점화식의 마지막 부분인

\sum_{\mathclap{i\le m\le j}} P_{m}

에 대한 이해도 필요하다.

이는 각각의 노드의 탐색 될 확률을 한 번 씩 더하는 것이다. 먼저 예시를 통해 이해를 해보자.

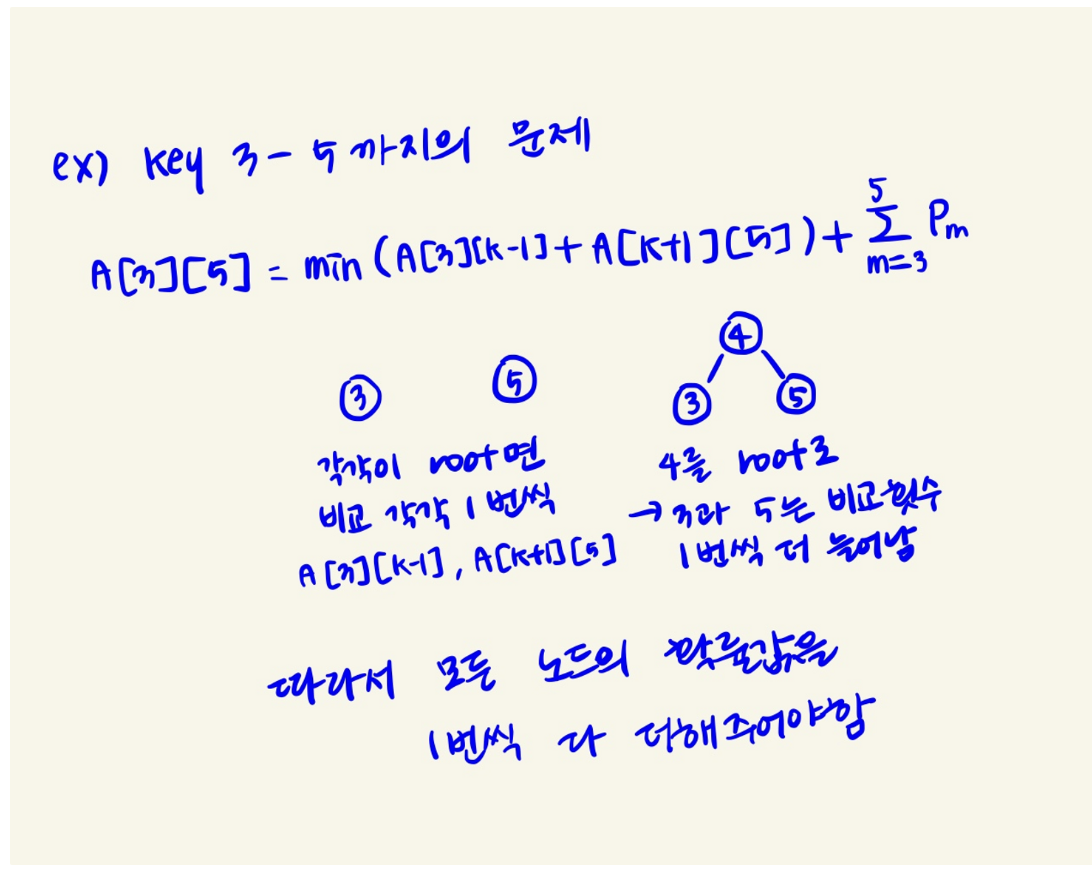
즉 각각의 key값들을 따로 떼어내서 보면, 각 독립적인 트리의 루트가 된다.

하지만 이 값들이 k가 루트가 됨에 따라 sub tree가 되면서 비교 횟수가 한 번 늘어나게 된다.

i부터 j까지의 모든 노드들이 이러하기 때문에 확률을 한번씩 더해주는 것이다.

예시를 통한 알고리즘의 이해

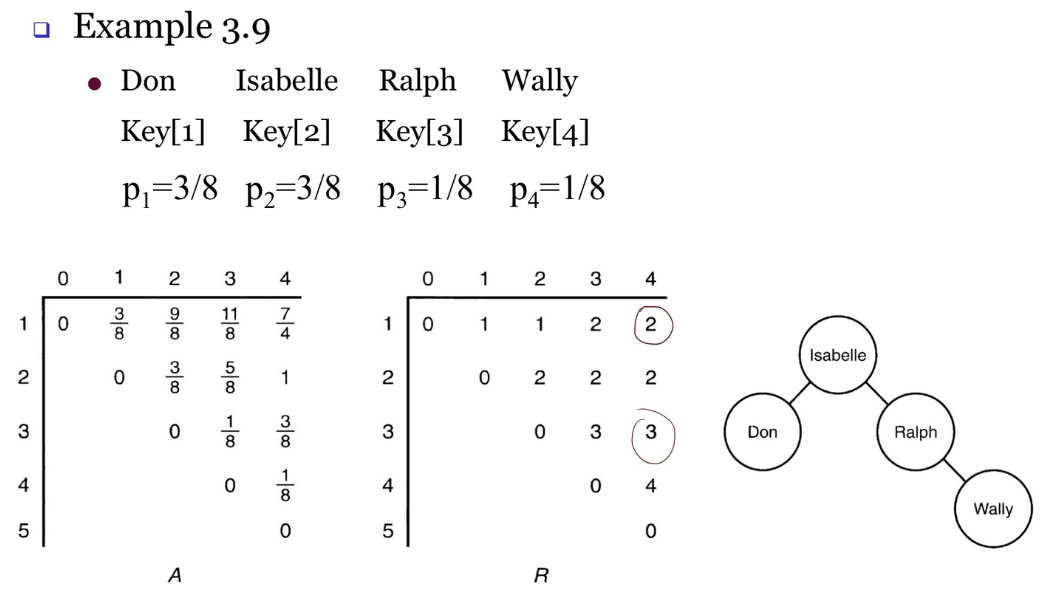
다음과 같은 예시가 있다.

각각 key값이 들어있는 배열 Key가 있고, 점화식을 통해 계산된 값을 저장하는 이차원 배열 A와

각각의 루트의 값을 저장하는 이차원 배열 R이 있다.

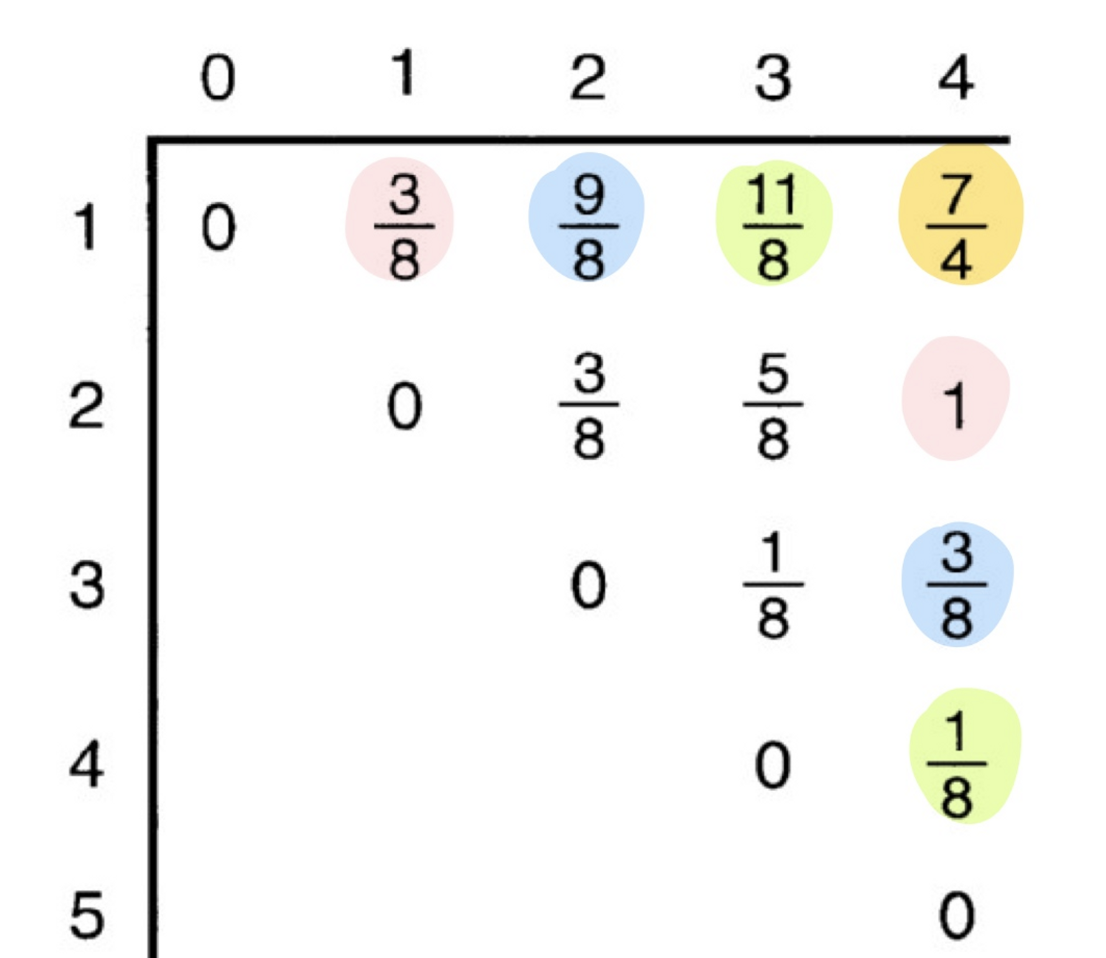
점화식에서 어떤 값을 구하기 위해(노란색으로 칠한 값) A배열의 값을 비교할 때는

같은 행, 같은 열의 값에서 같은 색으로 칠해진 값끼리 비교하고, 모든 확률을 한번씩 더해준다.

앞서 배웠던 행렬의 최소 곱셈 횟수 구하기와 같은 방식이다.

때문에 배열이 대각선 방향으로 채워지는 것을 알 수 있다.

알고리즘을 모두 수행하면 출력 결과를 바탕으로

optimal한 binary search tree를 구할 수 있어야 한다.

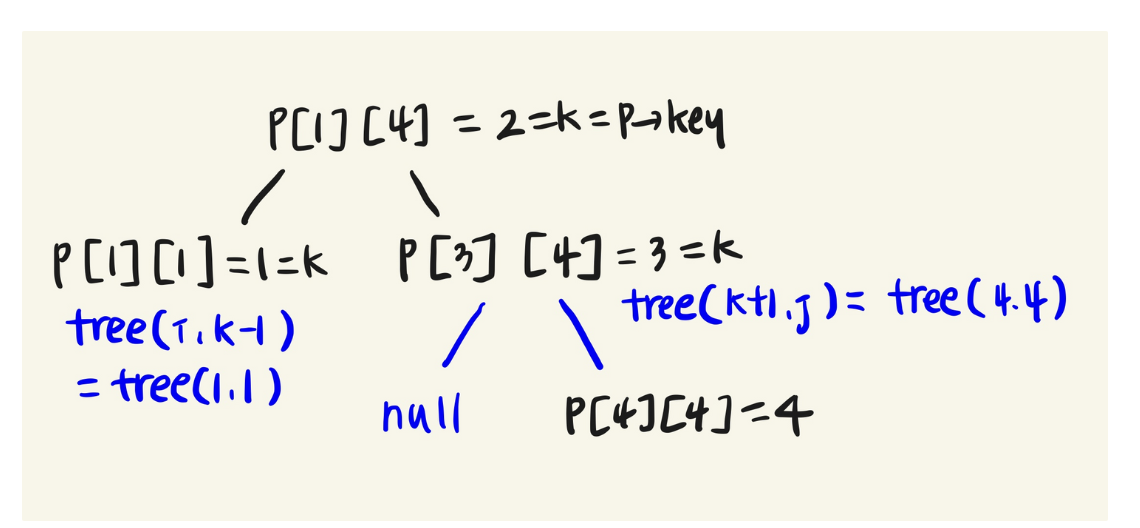
이에 대한 정보는 P배열에 들어있다.

아래 그림은 예시의 P배열을 보고 그린 optimal binary search tree이다.

Algorithm code

problem: 키를 가지고 있는 이진 탐색 트리를 결정한다.(키는 트리에 있다고 가정함)
inputs: 트리 포인터와 key값
outputs: key값을 갖고 있는 노드 포인터 p

#include <iostream>
#define MAX_F 987654336
using namespace std;

float add(float *p, int i, int j) {
  float sum = 0;
  for (int index = i; index <= j; index++) {
    sum += p[index];
  }
  return sum;
}

void optsearchtree(int n, float *p, float &minavg, int **R) {
  int i, j, k, diagonal;

  float **A = new float *[n + 1];
  for (int i = 1; i <= n + 1; i++)
    A[i] = new float[n + 1];

  for (i = 1; i <= n; i++) {
    A[i][i - 1] = 0;
    A[i][i] = p[i];
    R[i][i] = i;
    R[i][i - 1] = 0;
  }

  for (diagonal = 1; diagonal <= n - 1; diagonal++) {

    for (i = 1; i <= n - diagonal; i++) {
      j = i + diagonal;
      float minimum = MAX_F;
      for (int k = i; k <= j; k++) {

        if (A[i][k - 1] + A[k + 1][j] < minimum) {

          minimum = A[i][k - 1] + A[k + 1][j];

          A[i][j] = minimum + add(p, i, j);

          R[i][j] = k;
        }
      }
    }
  }
  minavg = A[1][n];
}
int main() {
  cout << "노드의 개수를 입력하세요." << endl;
  int n;
  cin >> n;
  cout << "각 노드의 가중치를 차례로 입력하세요. " << endl;
  float *p = new float[n + 1];
  for (int index = 1; index <= n; index++) {
    cin >> p[index];
  }
  int **R = new int *[n + 1];
  for (int i = 1; i <= n + 1; i++)
    R[i] = new int[n + 1];

  float minavg = 0;
  optsearchtree(n, p, minavg, R);

  cout << "answer: " << minavg << endl;
}