Depth-First Search 0-1 Knapsack Problem

0-1 Knapsack Problem의 특징

상태 공간 트리

만들고자 하는 모든 경우의 수가 상태 공간 트리에 펼쳐져야 한다.

⇒ sum of subset처럼 선택한 경우, 선택하지 않은 경우가 트리에 모두 그려져야 함.

왼쪽으로 가면 배낭에 물건을 넣은 경우, 오른쪽으로 가면 배낭에 물건을 넣지 않은 경우

변수

속성이 두개이기 때문에 두 가지 변수를 사용함

최적화 문제

상태 공간 트리를 이용하기는 하는데, 최적화 문제라서 답이 하나.

n-queens나 sum of sub-set, graph coloring은 그냥 모든 경우에 대해 다 출력해줌

⇒ 근데 얘는 딱 하나

최적 값을 저장하는 변수를 만들어 놓고 탐색을 하면서 최적 값을 계속 갱신한다.

그게 maxprofit이고 전역 변수다. ⇒ 마지막에 갱신한 것이 최적 답이 된다.

이건 backtracking 보단 branch and bound

기존 backtracking

유망하니? 근데 답이니?

답 아니야→ 자식 방문

답이야→ 답 출력

0-1 Knapsack problem

노드 v를 방문하고, v에서의 가치를 계산한다.

이게 현재까지 best(전역변수로 저장한 최종 답)보다 더 좋니?

더 좋으면 새로 방문한 값을 답으로 갱신하고 자식을 방문한다.

Branch and bound

bound는 한계치이다.

즉 branch and bound는 bound에 따라서 분기를 할지 말지 정해주는 것인데,

이 문제에서 bound는 ‘한계 이득’ 이다.

0-1 Knapsack Problem 동작 원리

변수

$w_i$ 와 $p_i$

각각 i번째 아이템의 무게와 값어치

값어치를 무게 값으로 나누어 무게 당 값어치가 큰 것부터 내림차순으로 정렬한다

⇒ greedy한 방식과 일부 닮아있지만, greedy는 아니다.

아래의 값들은 모두 각 노드에 대해 계산해야 하는 값이다.

profit

현재 노드까지 넣었던 아이템 값어치의 합

weight

그 노드까지 넣었던 아이템 무게의 합

Bound; Fractional knapsack

bound는 유망 여부를 판별하는 조건문에 사용되는 값이다.

노드가 level i에 있다고 하고 level k 에 있는 노드에서 총 무게가 W를 넘는다고 하자.

그러면 다음과 같이 bound를 구할 수 있다.

현재 노드에 오기 전까지 넣었던 무게와 i+1 level에서 k - 1level까지 얻을 수 있는 무게의 합을 더 한 것이 $totweight$ ⇒ 즉 배낭 용량을 넘기 전까지 다음 노드의 무게를 더해주는 것

$bound$는 현재 노드까지 넣었던 아이템 값어치의 합( $profit$ )과 i+1번째 노드 부터 k - 1번째 노드의 값어치는 모두 더해준다. ⇒ 왜냐하면 다 넣어도 배낭의 무게를 초과하지 않기 때문이다.

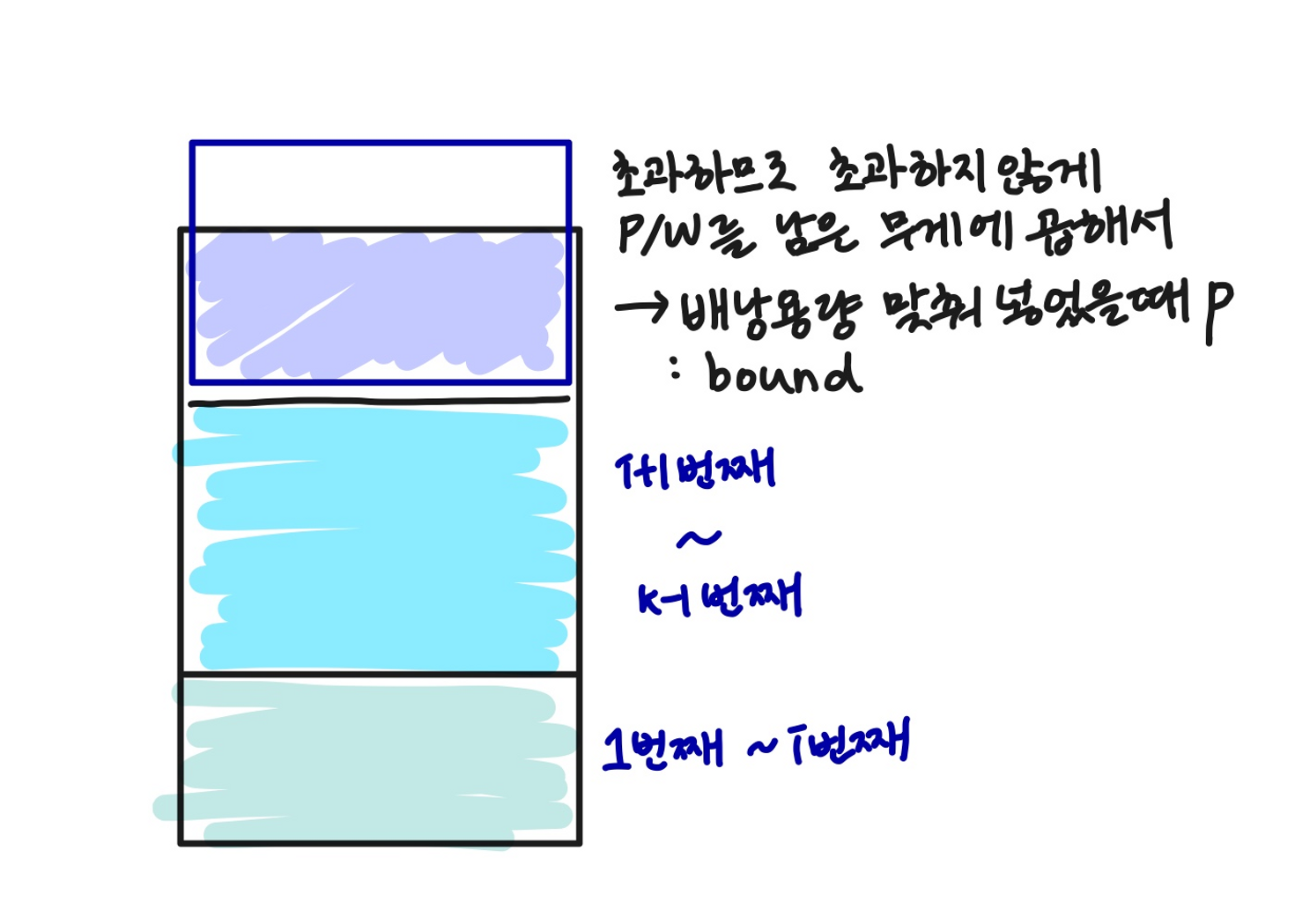
근데 k번째는 물건을 모두 다 넣으면 배낭의 용량을 초과하므로 배낭 용량에서 남아있는 값 만큼을 k번째 물건의 무게 당 가치와 곱하여 더해준다⇒ 이게 i번째 노드가 얻을 수 있는 한계 이득인 bound이다.

알고리즘이 어떻게 돌아가니

초기값

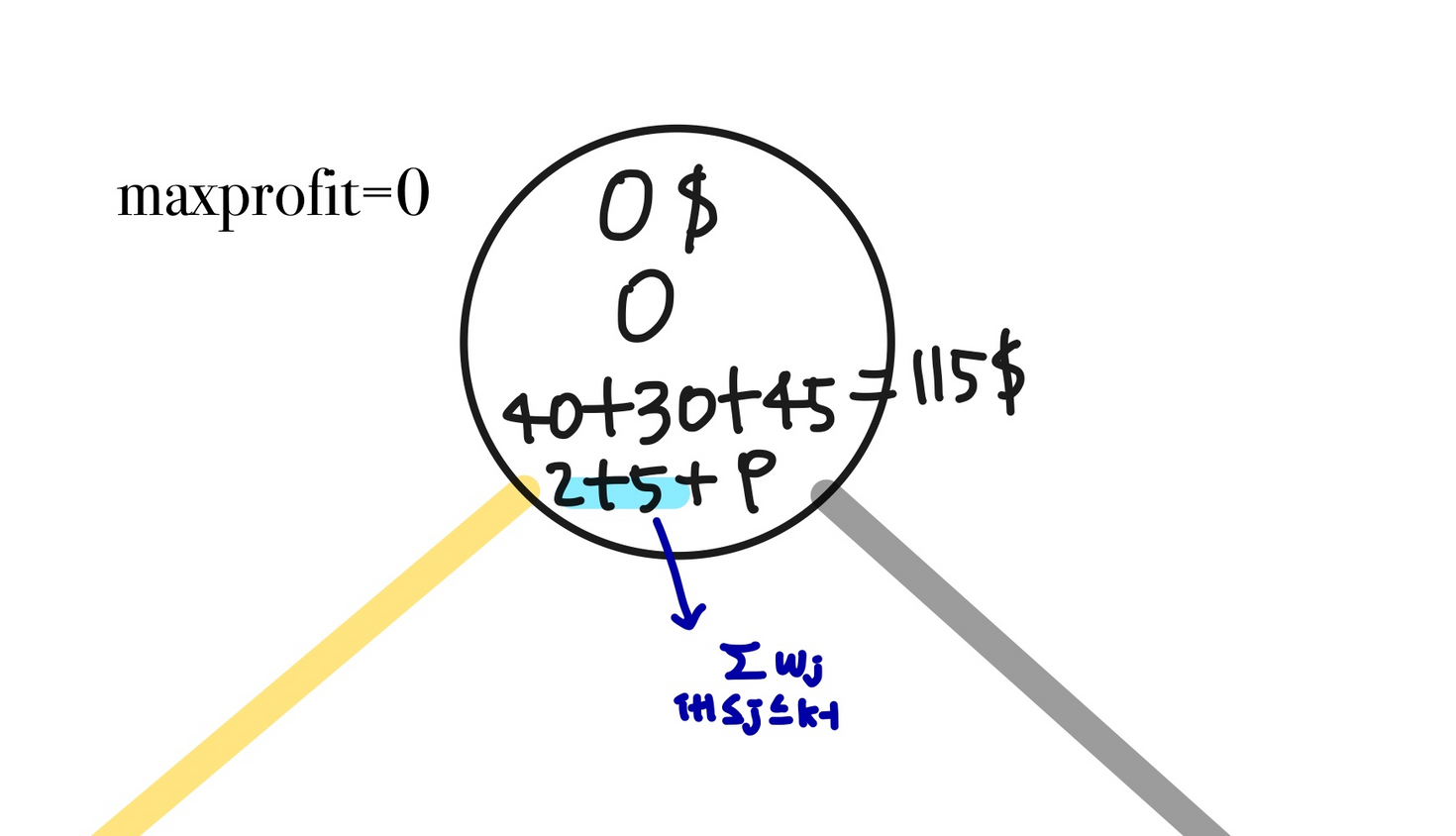
전역변수로 선언된 best값을 저장하는 maxprofit = 0, profit = 0, weight = 0 으로 초기화

bound도 계산해야 함.

진행 과정

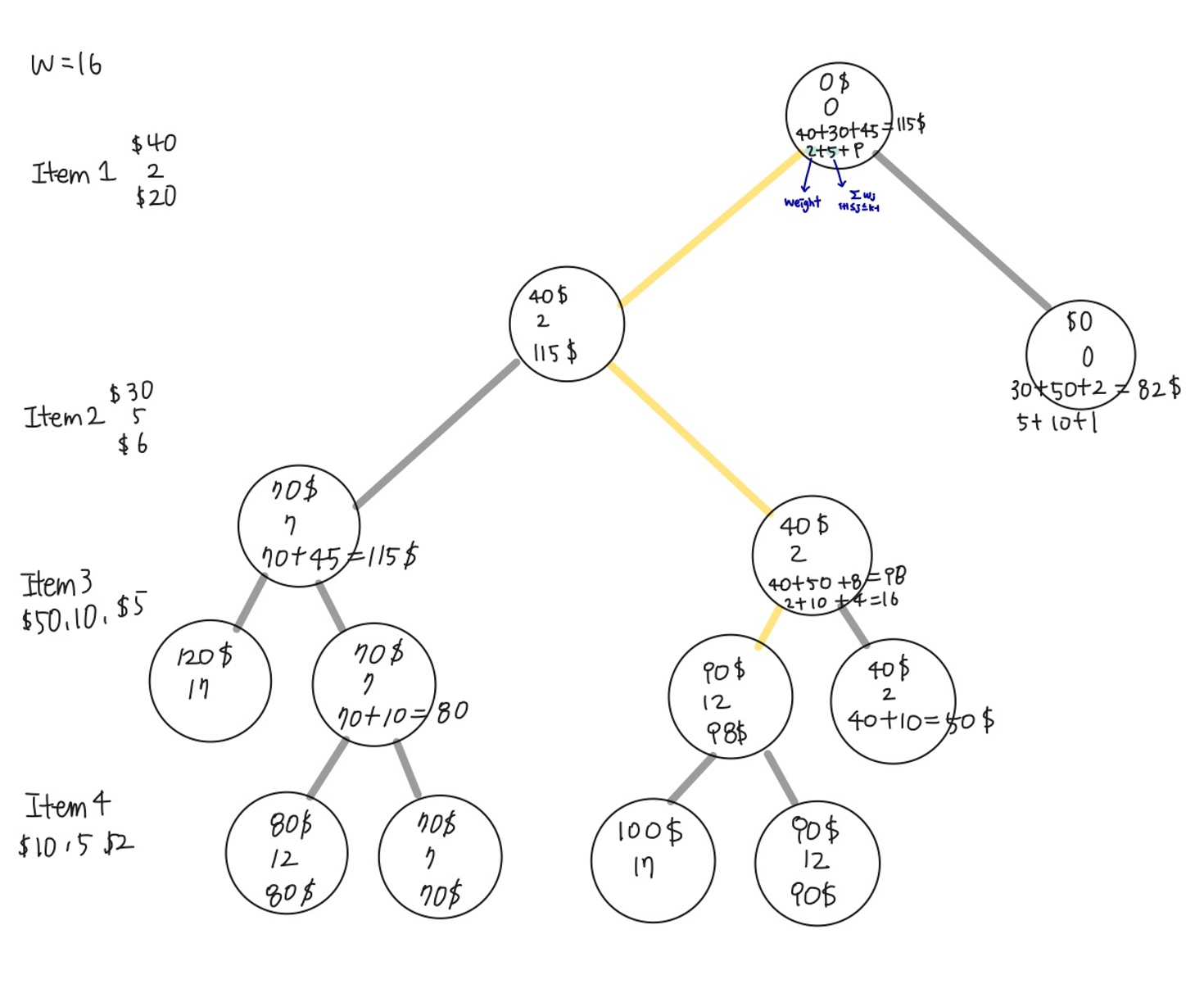
먼저 깊이 우선 탐색 방식으로 진행한다. 오른쪽으로 가면 그 레벨의 item을 가방에 넣지 않는 것이고, 왼쪽으로 가면 그 level의 item을 가방에 넣는 방식이다.

노드의 profit와 weight값을 계산한다.

그 노드의 bound값을 계산한다

weight<W이고, bound> maxprofit이면 유망하다.

유망한지 유망하지 않은지 판단하여 자식 노드 방문 여부를 정한다.

⇒모든 노드를 방문하지는 않음

Promising여부 판단

만약, weight가 전체 무게보다 크면 유망하지 않은 것

전체 무게 보다 작다면

1. 리프 노드에 갈때까지, 또는 배낭 용량을 넘지 않을 때 까지

   1. 계속 다음 노드의 무게를 더해서 totweight를 만듦
   2. 가치도 bound값에 더해줌

2. 배낭 용량을 넘었다면 그리고 넘은 무게 값을 가진 노드가 리프 노드거나, 리프노드보다 위에 있다면

   1. bound = bound + (W - totweight) * p[k]/ w[k];

3. bound가 maxprofit보다 크면 true를 return해준다.

   ⇒ bound가 maxprofit보다 커야 유의미한 값이다.

   기껏 검사해서 갔는데, 현재 최선의 값보다 더 작은 값이라면 굳이 갈 필요가 없다.

Pseudo code

• problem: 무게와 가치를 가진 n개의 아이템이 있을 때, 배낭의 용량도 주어진다. 주어진 item중에 배낭 무게를 넘지 않으면서 최고의 이익을 가지는 item의 집합을 구하여라.
  
• input: n, W, w[1~n], p[1~n]. w와p는 무게 당 가치 값으로 비오름차순으로 정렬 되어 있다.
• output: bestset[1-n] 포함되면 YES, 포함되지 않으면 NO를 출력한다.

#include <iostream>
using namespace std;

int weight;
int profit;

bool promising(int i) {
  int j, k;
  int totweight;
  float bound;
  if (weight >= W)
    return false;
  else {
    j = i + 1;
    bound = profit;
    totweight = weight;
    while ((j <= n) && (totweight + w[j] <= W)) {
      totweight = totweight + w[j];
      bound = bound + p[j];
      j++;
    }
    k = j;
    if (k <= n)
      bound = bound + (W–totweight) * p[k] / w[k];
    return bound > maxprofit;
  }
}

void knapsack(int i, int profit, int weight) {
  if (weight <= W && profit > maxprofit) { // best so far
    maxprofit = profit;
    numbest = i;
    bestset = include;
  }
  if (promising(i)) {
    include[i + 1] = “YES”; // Include w[i+1]
    knapsack(i + 1, profit + p[i + 1], weight + w[i + 1]);
    include[i + 1] = “NO”; // Not include w[i+1]
    knapsack(i + 1, profit, weight);
  }
}

분석

최악의 경우

• W = n
• $p_i$ = $1$, $w_i$ = $1$ ⇒ $1≤ i ≤ n-1$ 일때
  
• $p_n = n$, $w_n = n$

n-1번째까지 전부 다 더해도, W를 넘지 않기 때문에 모두 유망할 것이다.

bound는 계속 n이 될 것이다. 중간에 몇 개를 더하지 않았다 해도 n이 마지막에 다 채워주기 때문에

maxprofit은 n-1까지 다 더하는 것이 제일 크기 때문에 중간에서 바꿀 수 없을 것이다.

n-1 level이 모두 유망하기 때문에, n level도 다 방문하게 될 것이다.

→ 답은 트리의 맨 오른쪽 아래의 왼쪽 노드( 마지막만 선택하는 경우)

⇒ $2^n$