Graph Coloring Problem

Graph Coloring이 뭐임?

• m-coloring: m개의 색을 가지고 인접한 지역이 같은 색이 되지 않도록 지도에 색칠하는 문제
  

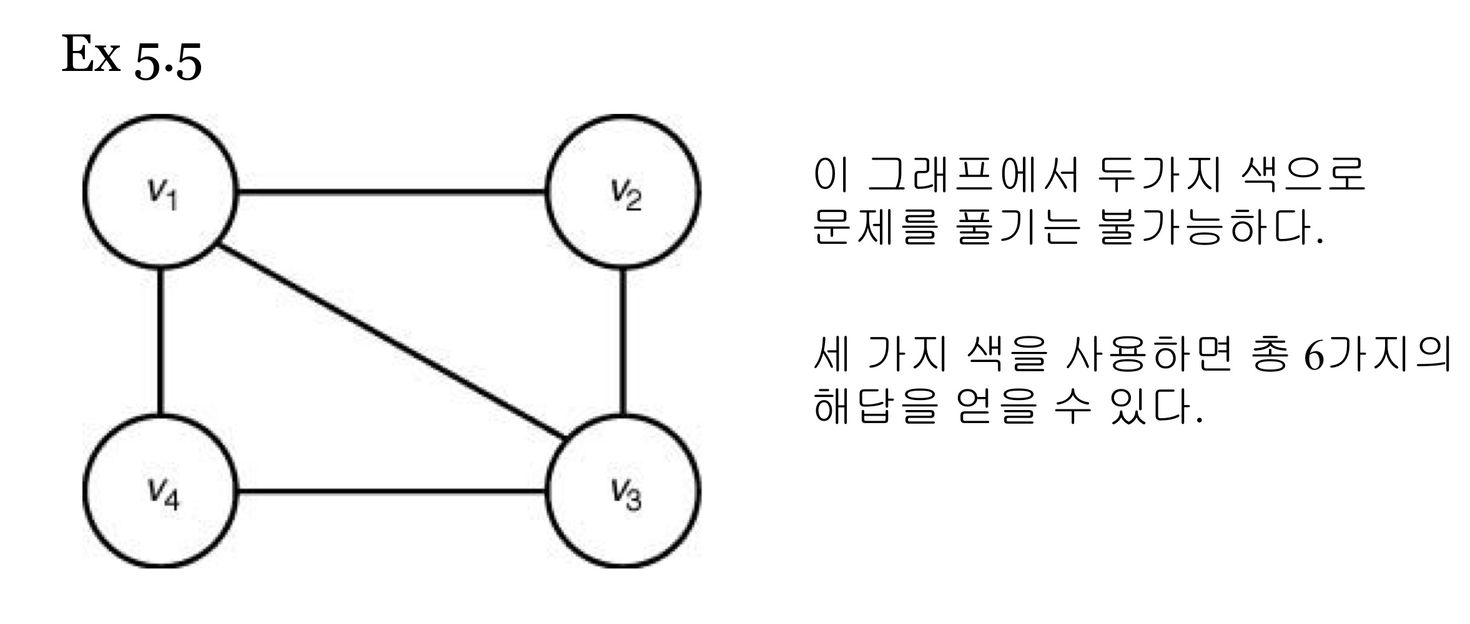
용어 정리

평면 그래프

• 지도에서 각 지역을 그래프의 정점으로 하고, 한 지역이 어떤 다른 지역과 인접해 있으며, 그 지역들을 나타내는 정점들 사이에 이음선을 그으면, 모든 지도는 그에 상응하는 평면 그래프로 표시할 수 있다.
  

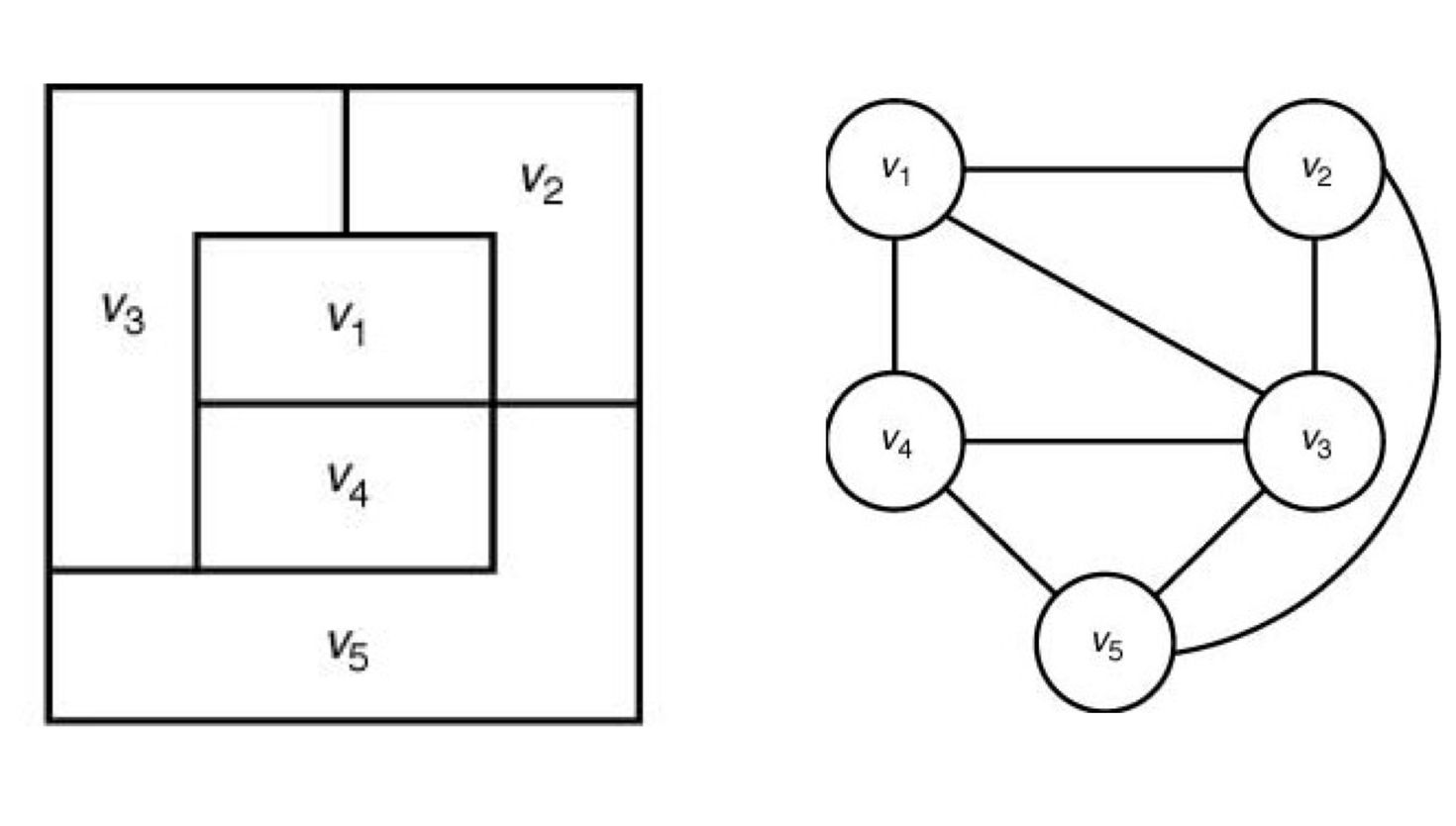
backtracking 방법으로 풀기

• problem: m개의 색을 사용하여, 그래프의 정점의 색을 할당할 수 있는 모든 방법을 결정하라. 단, 인접한 정점은 서로 같은 색을 가질 수 없다.
  
• input: 정점의 수 n, 색의 수 m, W[1~n][1~n]( bool형 그래프 → true면 i와 j 사이에 간선이 있는 것)
• output: vcolor[1~n]

상태 공간 트리 구성하기

$m^{level수}$ 만큼의 노드가 한 level에 생긴다.

파란색, 노란색, 빨간색을 선택할 수 있다면

→ 각각 노드에 대해 파란색을 선택하는 경우, 빨간색, 노란색을 선택하는 경우

Promising 판별하기

W[i][j] && (vcolor[i] == vcolor[j])

pseudo code

void m_coloring (index i)
{
		int color;
		if(promising(i))
				if(i == n) cout<< vcolor[1] ~ vcolor[n];
				else{
						for(color = 1; color <= m; color++;){
								vcolor[i+1] = color;
								m_coloring(i+1);
				}
}

bool promising(index i){
		int j;
		bool change;
		
		change = true;
		j = 1;

		while(j<i && change)
		{
				if(W[i][j] && (vcolor[i] == vcolor[j]))
						change = false;
						j++;
		}
		return change;
}

분석하기

최악의 경우

$v_1$ ~ $v_{n-1}$ 까지는 모두 $v_n$에 연결되어있지만, $v_1$ ~ $v_{n-1}$ 각 노드들 서로는 연결 되지 않았다.

단, $v_{n-2}$ 와 $v_{n-1}$ 사이에 간선이 하나 있다.

이때 $m = 2$이다.

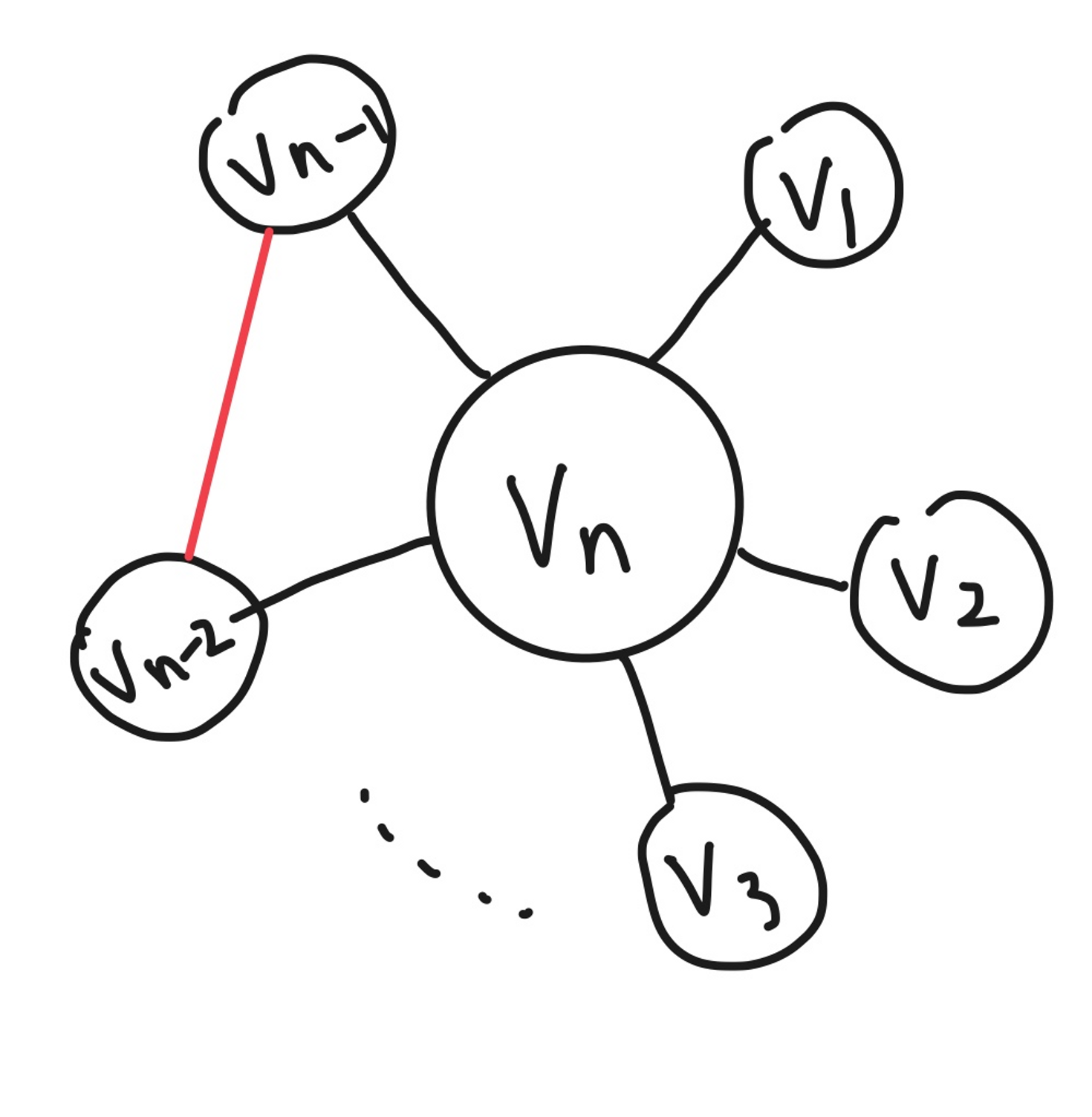
상태 공간 트리 상의 노드의 총 수는

최악의 경우 노드를 총 몇 개 방문하는지 살펴보자

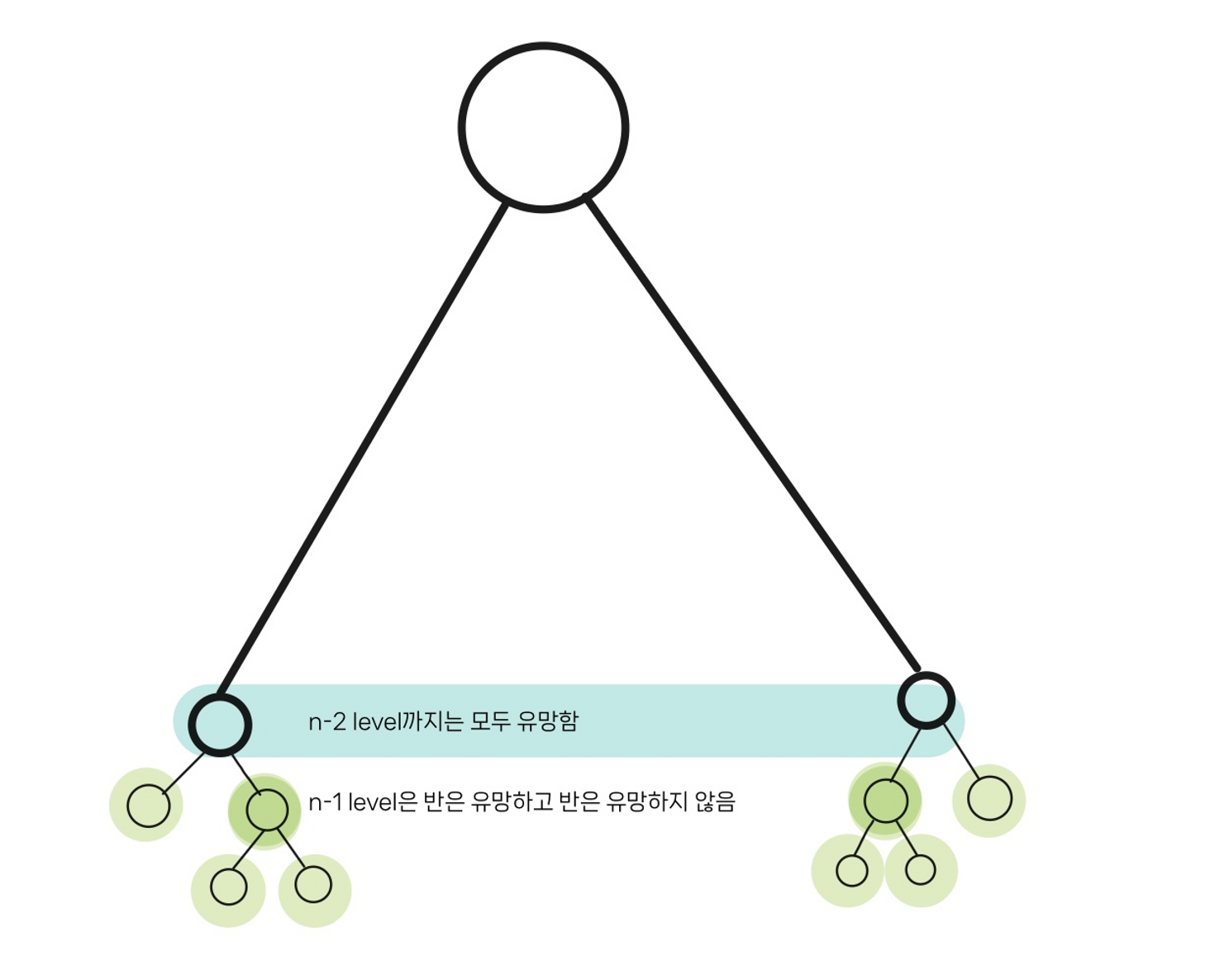
(v 생략)

첫번째로 1~n-2번째 노드들은 모두 유망하고, 모두 방문한다.

다음으로는 n-1번째 노드들은 모두 방문 하지만, 반만 유망하다.

⇒ n-2와 연결되어있으므로 같은 색은 사용하지 않아야 하기 때문에

마지막으로 n번째 노드이다. 이들은 유망했던 n-1번째 노드들의 자식들만 방문하므로

n level의 노드의 절반만 방문하게 된다.

하지만 답을 찾을 수 없으므로, 알고리즘은 답을 출력하지 않고 종료된다.

따라서 방문하는 노드의 수는 $2^n-1 + 2^{n-1}$ 개 일 것이다.