Dijkstra’s algorithm

Dijkstra’s algorithm

가중치가 있는 방향성 그래프에서 한 특정 정점에서 다른 모든 정점으로 가는

최단 경로를 구하는 문제이다.

최단 경로 구하는 문제면, 플로이드랑 똑같은거 아님?

아니다.

플로이드는 모든 노드가 출발지가 될 수 있지만, 다익스트라는 v1만 출발점으로 둘 수 있다.

prim이랑 똑같다!

Pseudo Code

prim알고리즘처럼 반복문이 총 N-1회 수행된다. N은 노드의 수

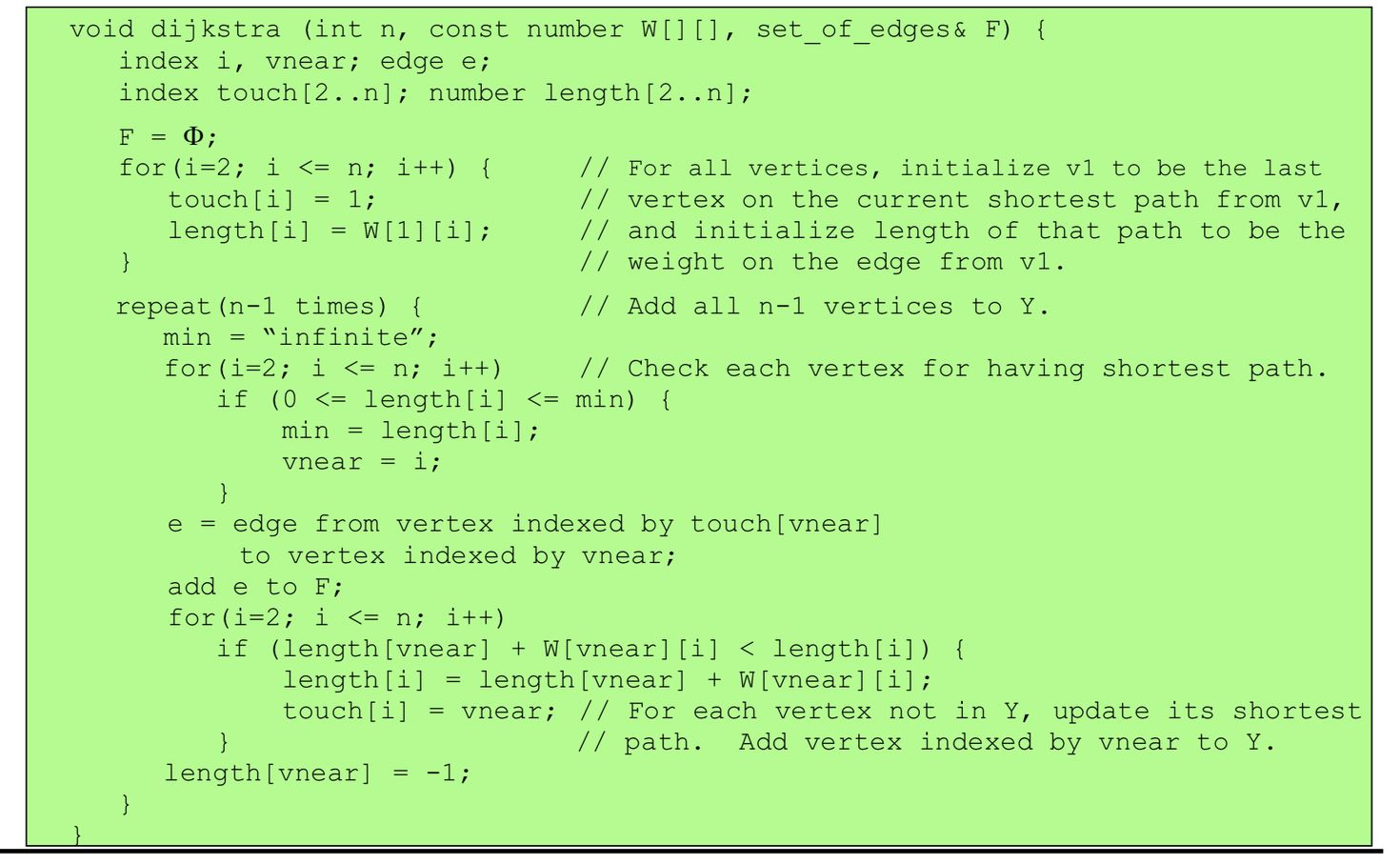
알고리즘에서 사용되는 변수, 용어 정리

• touch배열: 각 index에서 가장 가까운 node의 index 번호
• length배열: prim에서 distance[i]는 edge하나의 길이인데, 여기에서는 1부터 자기 자신까지 edge들의 합이다.
  
• W배열: 인접 행렬로 나타낸 방향 그래프

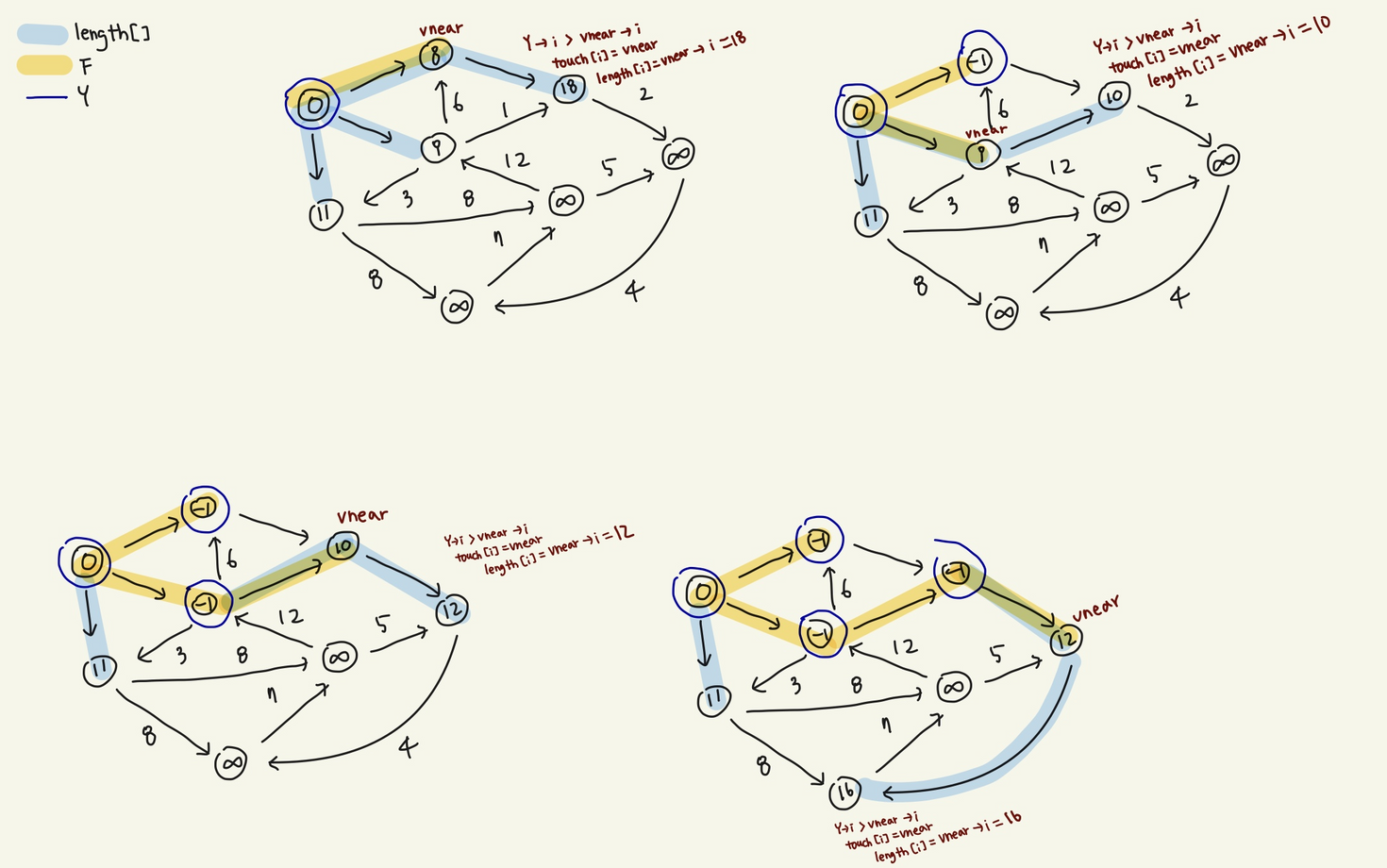
알고리즘 동작 원리 이해하기

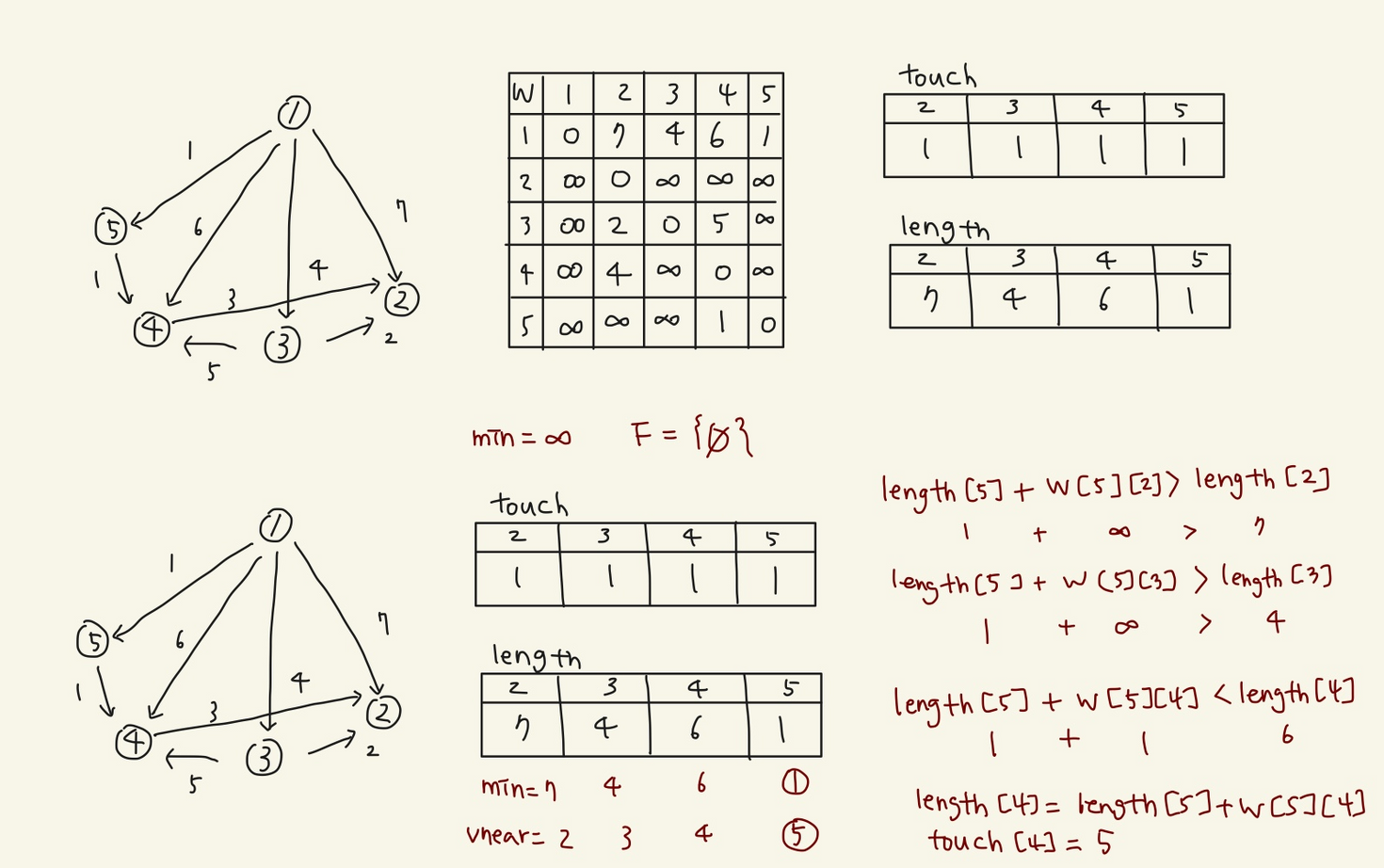
반복문의 첫번째 수행과정만 나타낸 손계산

• n-1번을 돌면서 length배열을 비교하여 현재 Y에 있는

  노드에서 가장 가까운 노드를 vnear로 고른다.
  

• vnear로 고른 노드와 Y를 잇는 간선을 F에 넣고

• Y와 V-Y의 거리를 update해준다.

  • vnear로 선택한 노드에서 i로 가는 길이와 그 전 Y집합에서 i로가는 길이 비교
  • 만약 vnear에서 가는게 더 가까우면 length[i]를 vnear로 선택한 노드에서 i로 가는 길이로 update해주고
  • touch[i]도 vnear로 바꿔줌

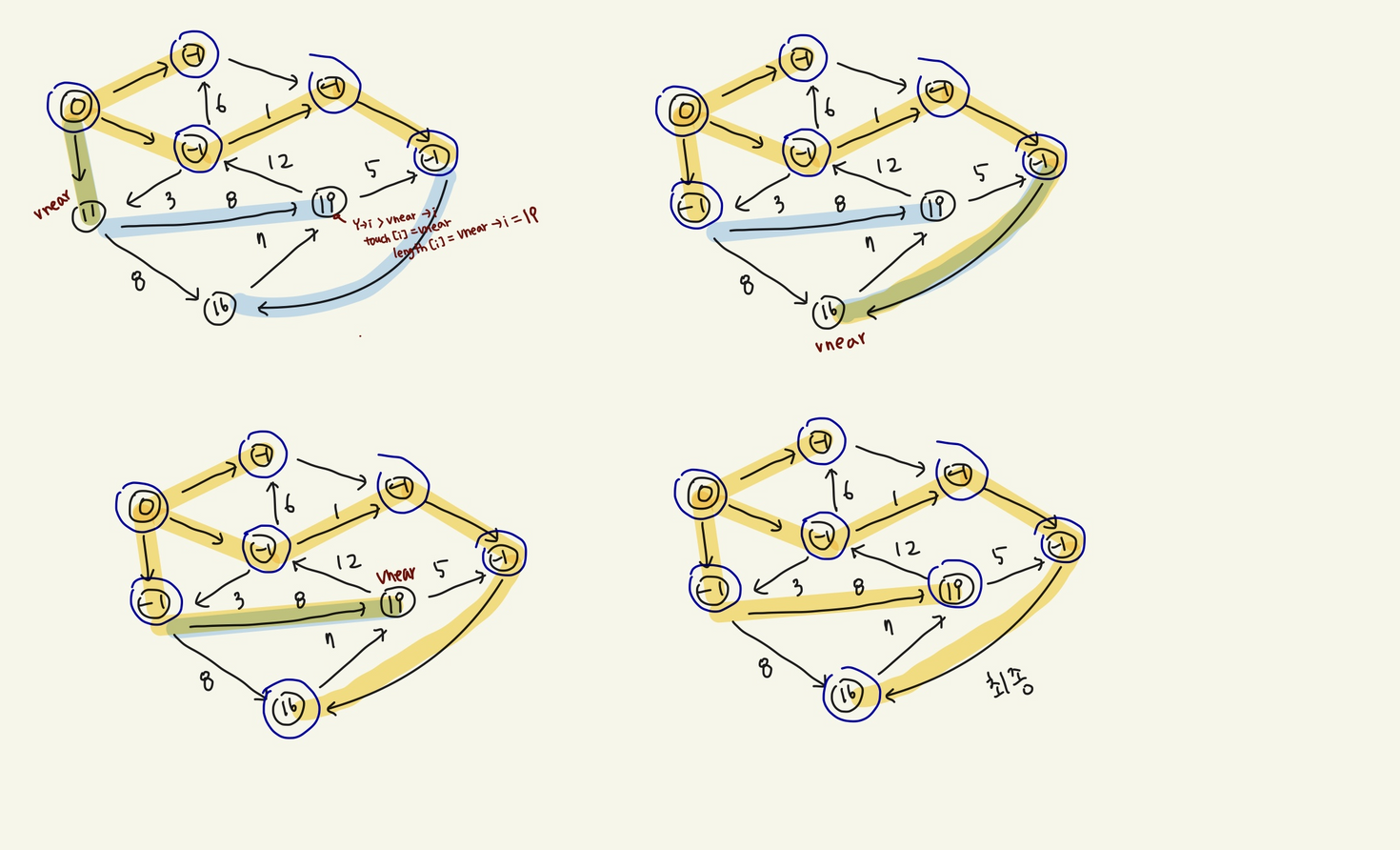
• 그리고 선택된 vnear의 length값은 -1로 둔다.

• 마지막 touch 배열을 보면, touch[i]→i로 간선이 연결되어

  각 간선만 그래프에서 남겨두면

  v1에서 각 노드까지의 최단 경로를 알 수 있도록 함.
  

배열 없이 설명하는 다익스트라 동작 원리

분석하기

$T(n) = 2(n-1)^2 \in \theta(n^2)$