The Knapsack Problem
The Knapsack Problem
S = {item, item, … }
w = weight of item
p = value of item
W = maximum weight of items in the knapsack
위의 식을 만족하면서
가 최대가 되도록 가 되는 A를 결정하는 문제이다.
즉, 배낭에 넣을 수 있을만큼 물건을 넣되,
그 가치의 합이 가장 큰 답을 구하는 문제이다.
왜 탐욕적 알고리즘을 쓰는 걸까?
brute force 방식
n개의 물건에 대해서 모든 부분 집합을 다 고려하게 되므로
크기가 n 인 집합의 부분 집합 수는 이다.
따라서 지수 시간 복잡도 이므로 비 효율적이다.
DP
최적화 문제를 푸는데 조금 더 적합한 알고리즘으로,
때로는 불필요하게 복잡하다.
단일 출발점 최단 경로 문제의 시간 복잡도는 이다.
최적화 원칙이 적용되는지 점검하면 된다.
배낭 문제에는 0-1 배낭 문제가 적합하다.
Greedy
최적화 문제를 푸는 데에 있어 적합하다.
다른 알고리즘이 존재할 경우에, 보통의 경우 더 효율적이다.
단일 출발점 최단 경로 문제의 시간 복잡도는 이다.
알고리즘이 최적인지를 최적 여부 증명을 통해 밝혀야 한다.
배낭 채우기 문제만 풀 수 있다.
The 0-1 Knapsack Problem
배낭에 넣을 아이템을 쪼갤 수 없다.
1) Greedy 1

W = 30이라고 가정한다.
비싼 물건부터 우선적으로 채운다.
이 경우 item_1만 담아, 총 값이 10$가 된다.
하지만 최적의 경우는 item_2 + item_3 ⇒ $18 이다.
2) Greedy 2
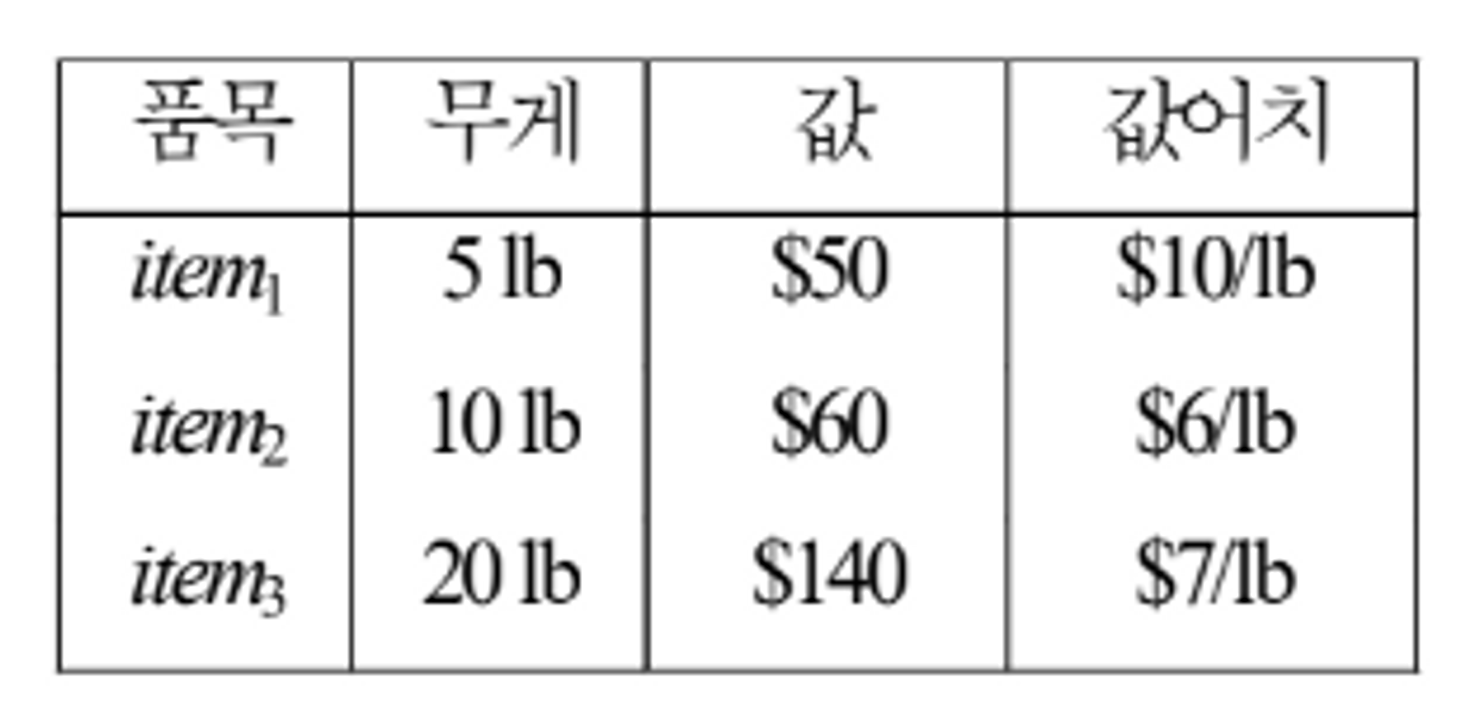
W = 30이라고 가정한다.
무게 당 가장 가치가 높은 물건부터 우선적으로 채운다.
이 경우 item_2 + item_3 ⇒ 190$ 이 된다.
하지만 최적의 경우는 item_2 + item_3 ⇒ 200$ 이다.
3) DP로 풀어보는 0-1 Knapsack Problem
점화식
이고 일때, 전체 무게가 를 넘지 않도록 번째 까지의 항목 중에서 얻어진 최고의 이익을 라고 하면
점화식 첫번째 줄의 의미
-
같은 열의 앞 행과 i번째 물건의 가치가 현재까지 선택된 것들 보다 큼
-
i번째 물건의 가치와 앞 행에서 (현재까지 선택된 무게 - i번째 물건)을
열로 가지는 요소의 값을 더한 값 : 방금까지 선택된 물건에 i번째 물건을 더함
즉, 쉽게 말하면 현재까지 선택된 것이랑 지금 선택한 것을 더한 값, 지금 선택한 것 중에 가치가 더 큰 것을 고르는 것이다.
점화식 두번째 줄의 의미
나머지는 그냥 앞 행과 똑같이 함
4) DP의 정제
n과 W와는 아무상관 관계가 없다. 만약에 W가 n!의 값을 갖는다면 시간 복잡도는 n X n!이 되므로
무작정 알고리즘 보다 나은 것이 없다.
이후 백트래킹에서 배우는 것 같다.
- n-1번째 행에서는 P[n-1][W]와 P[n-1][W- $w_n$]항만 필요하다.
- i번째 행에서 어떤 항목이 필요한지 결정하고, i-1번째 행에 필요한 항목을 결정함
- P[i][w] ⇒ P[i-1][w]와 P[i-1][w- $w_i$]로 계산 가능
- 손 계산 하면서 느꼈던 의문점: 왜 P[2][20]은 계산하지 않는거임? ⇒ 개선된 DP방식이기 때문에 메모이제이션을 통해 계산한다. ⇒ Topdown
때문에 최종 답에 대한 필요한 부분만 계산하고 기억하므로 P[2][20]은 계산하지 않는다 이게 맞는지 모르겠지만 추측이 그렇다.
- 분석
- n-i 열에서 번 계산한다.
- 따라서 총 1부터 번을 더해주어야 하므로, 번 계산을 수행한다.
- 최악의 경우의 수행 시간은 이다.
- 앞서 정제되지 않았던 알고리즘의 수행 시간과, 정제된 알고리즘의 수행 시간을 비교해보면, W에 따라 둘 중에 최소가 되는 값이 달라지는 것을 알 수 있다.
- 분할 정복 방법도 이 알고리즘 설계가 가능한데, 이때도 최악의 수행 시간은 이다.
NP
아무도 이 문제를 해결 할 수 있는 알고리즘의 최악의 경우 수행 시간이
지수보다 나은 것을 발견하지 못했고
그러한 알고리즘이 없다고 증명한 사람도 없는 문제
NP-Complete
한 문제 풀면 이런 종류 문제가 다 풀림
The Fractional Knapsack Problem
물건의 일부분을 잘라서 담을 수 있다. Greedy하게 최적 해를 구하는 알고리즘을 만들 수 있다.
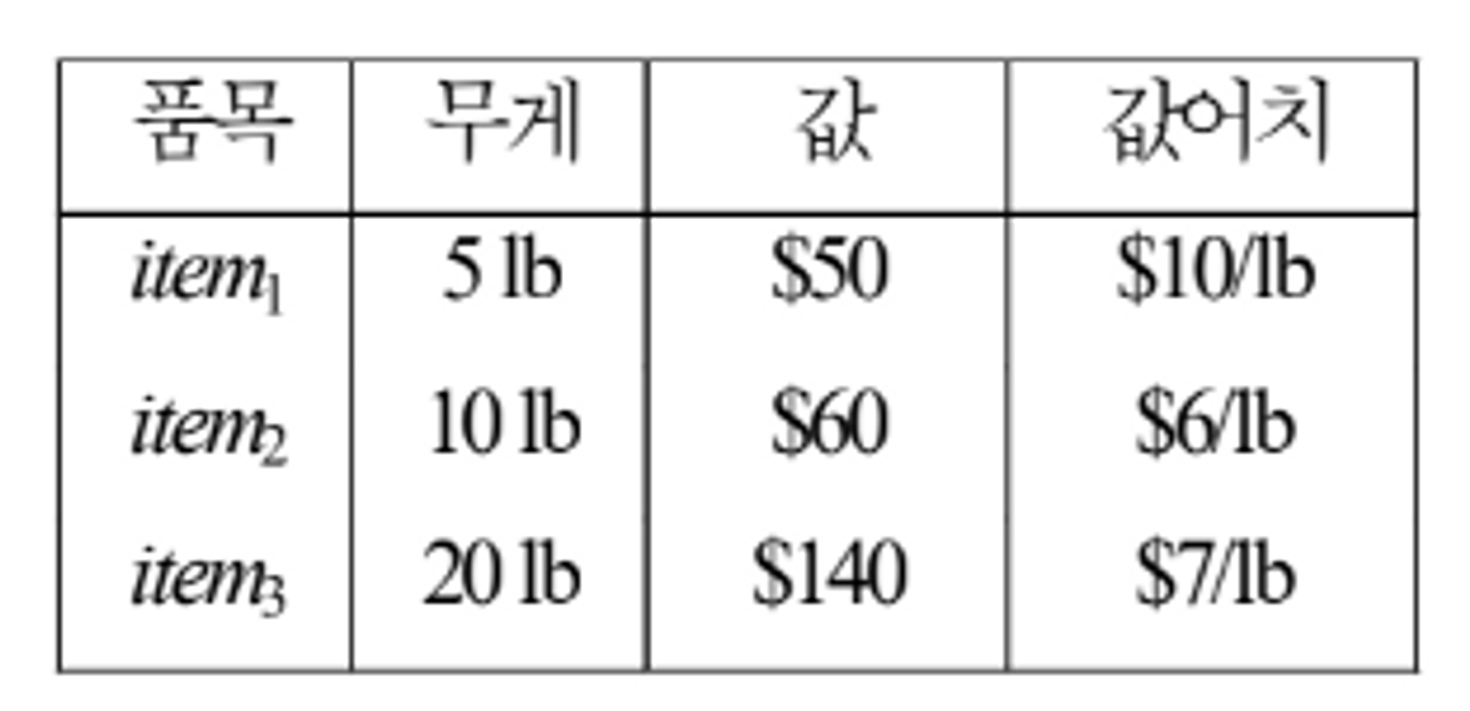
W = 30이라고 가정한다.
+ + (5/10) = $50 + $140 + (5/10)$60 ⇒ 최적
