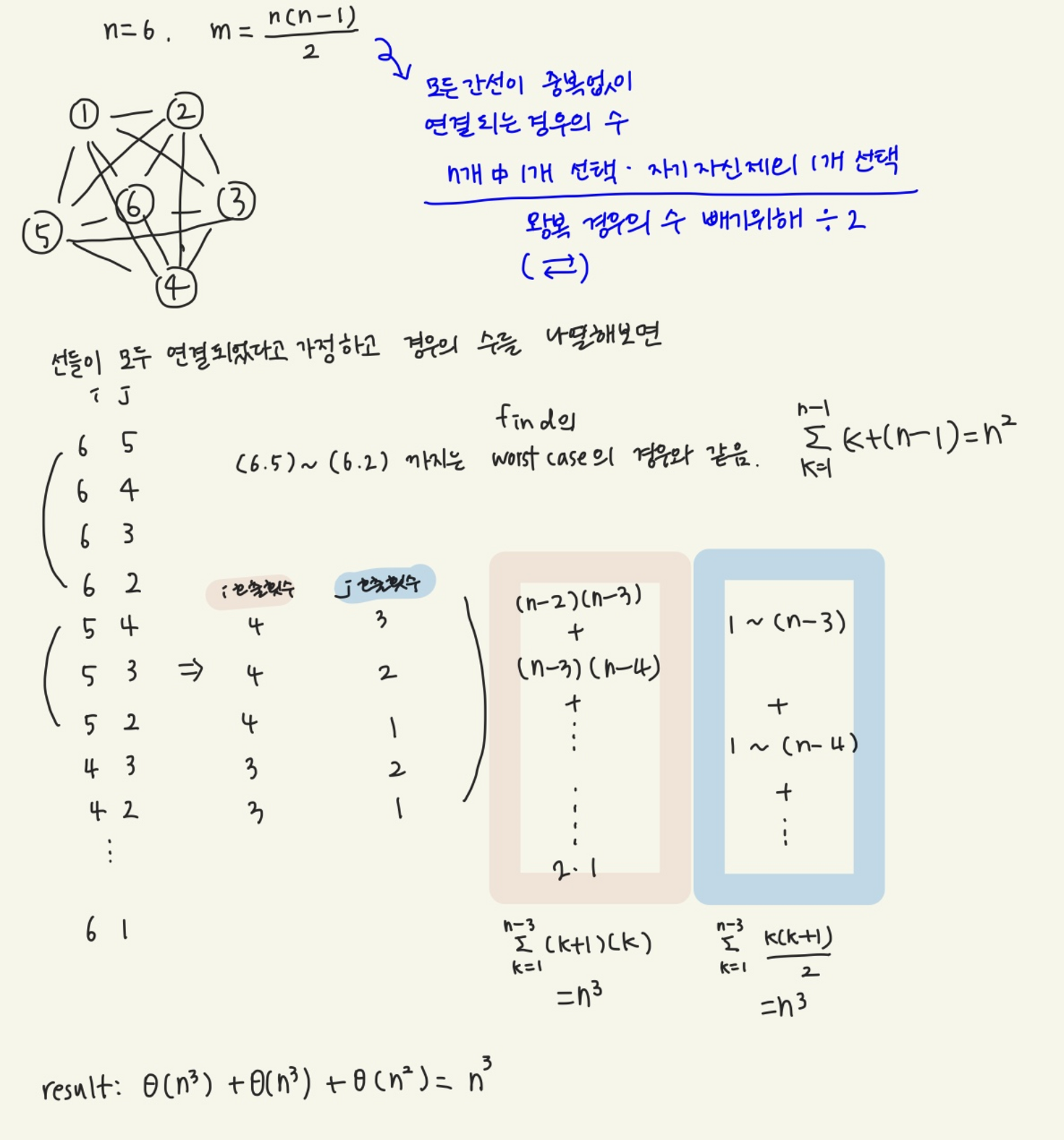
Kruskal’s algorithm

알고리즘에서 사용되는 자료형과 용어

서로소 집합 추상 데이터 타입

• 서로소란 두 집합간 공통된 부분이 없는 집합

index i; set_pointer p, q;

initial(n): n개의 서로소 부분 집합을 초기화 함

p = find(i): i가 포함된 집합의 포인터를 넘겨준다.

merge(p,q): 두개의 집합을 가리키는 p와 q를 합병한다.

equal(p,q): p와 q가 같은 집합을 가리키면 true를 넘겨준다.

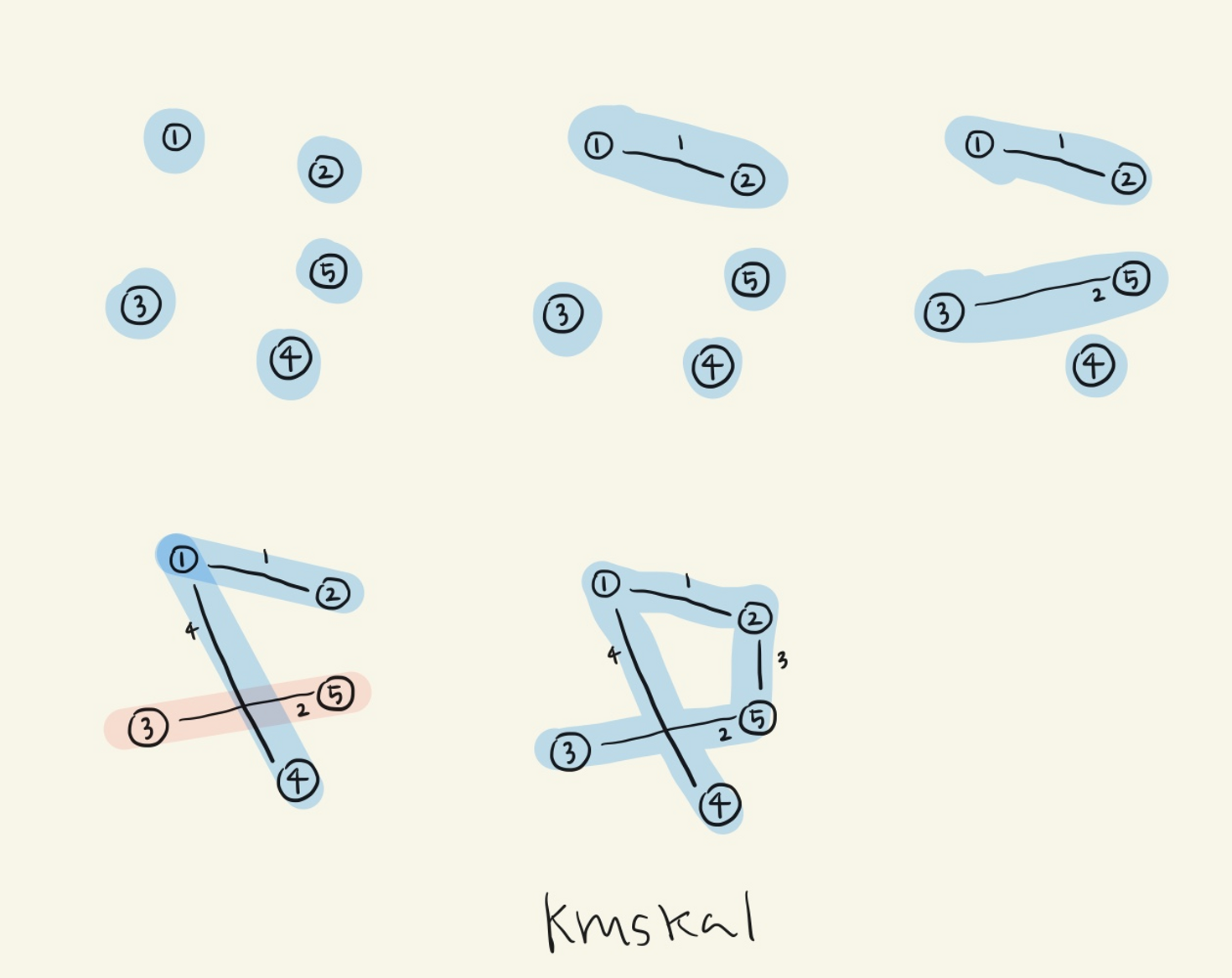
알고리즘의 작동 원리

#include <cstdlib>
#include <iostream>
using namespace std;

typedef struct {
    int v1;
    int v2;
    int weight;
} edge;

typedef int index;
typedef index set_pointer;

typedef struct {
    index parent;
    int depth;
} universe;

int m;
universe* U = new universe[m + 1];

int cmpfunc(const void*, const void*);
void initial(int);
void makeset(index);
set_pointer find(index);
bool equal(set_pointer, set_pointer);
void merge(set_pointer, set_pointer);
void kruskal(int, int, edge*, edge*);

void kruskal(int n, int m, edge* E, edge* F) {
    index i, j;
    set_pointer p, q;
    edge e;

    index index_f = 0;
    index index_e = 0;
    qsort(E, m + 1, sizeof(e), cmpfunc);

    for (int k = 1; k <= m; k++) {
        cout << k << "번째: " << E[k].v1 << "-" << E[k].v2 << "," << E[k].weight << endl;
    }

    //F초기화
    for (int i = 1; i <= m; i++) {
        F[i].v1 = 0;
        F[i].v2 = 0;
        F[i].weight = 0;
    }
    //각 노드가 트리 하나의 root
    initial(n);

    while (index_f < n - 1) {
        cout << "\n\n\nindex_f: " << index_f << endl;
        e = E[++index_e];
        i = e.v1;
        j = e.v2;
        cout << "i: " << i << "  j: " << j << endl;
        cout << "\n";
        cout << "\nfind i: " << endl;
        p = find(i);

        cout << "\n\nfind j: " << endl;
        q = find(j);
        if (!equal(p, q)) {
            cout << "\n\np와 q는 다르므로 merge" << endl;
            merge(p, q);
            F[++index_f] = e;
        }
        cout << "\n\nU배열: ";
        for (int k = 1; k <= n; k++) {
            cout << U[k].parent << "-" << U[k].depth << ", ";
        }
    }
}

int main() {
    int n;
    cout << "정점의 수를 입력하세요: ";
    cin >> n;
    cout << "간선의 수를 입력하세요: ";
    cin >> m;
    edge* E = new edge[m + 1];
    edge* F = new edge[n + 1];
    cout << "정점 1, 정점 2, 가중치를 차례대로 입력하세요" << endl;
    for (int k = 1; k <= m; k++) {
        int a, b, c;
        cin >> a >> b >> c;
        E[k].v1 = a;
        E[k].v2 = b;
        E[k].weight = c;
    }

    kruskal(n, m, E, F);

    cout << "\n\n=============answer==============" << endl;;
    for (int k = 1; k <= n - 1; k++) {
        cout << F[k].v1 << "-" << F[k].v2 << endl;
    }
}

int cmpfunc(const void* a, const void* b) {
    if (((edge*)a)->weight <= ((edge*)b)->weight)
        return -1;
    else return 1;
}

void initial(int n) {
    index i;
    for (i = 1; i <= n; i++)
        makeset(i);
}

void makeset(index i) {
    U[i].parent = i;
    U[i].depth = 0;
}

set_pointer find(index i) {
    index j;
    j = i;
    while (U[j].parent != j) {
        cout << "find함수에서 j: " << j << endl;
        j = U[j].parent;
    }
    return j;
}

bool equal(set_pointer p, set_pointer q) {
    if (p == q)
        return true;
    else
        return false;
}

void merge(set_pointer p, set_pointer q) {
    if (U[p].depth == U[q].depth) {
        cout << "\n\nU[p]와 U[q]의 depth가 같으므로 ";
        cout << "U[p].depth = " << U[p].depth << " + 1 = ";
        U[p].depth = +1;
        cout << U[p].depth << endl;
        U[q].parent = p;
        cout << "U[" << q << "].parent = " << U[q].parent << endl;
    }
    else if (U[p].depth < U[q].depth) {
        cout << "\n\nU[p].depth < U[q].depth 이므로";
        U[p].parent = q;
        cout << "U[" << p << "].parent = " << q << endl;
    }
    else {
        cout << "\n\nU[q].depth < U[p].depth 이므로";
        U[q].parent = p;
        cout << "U[" << q << "].parent = " << p << endl;
    }
} 

먼저 간선들을 가중치를 기준으로 비 내림차순으로 정렬해야 한다.

F는 공집합으로 초기화 하고 U도 초기화 한다 .

각 노드들은 자기자신이 루트인 트리로 초기화 된다.

가중치를 기준으로 정렬된 간선들의 집합[1]을 고르고, 각각 i와 j를 간선과 연결된 노드로 설정한다. find(i)와 find(j)를 실행하면, 각 트리의 root값을 알 수 있다.

만약 트리의 루트 값이 다르다면, merge로 두 트리를 합친다

만약 depth가 같다면 p가 q의 부모 노드가 되고, p의 깊이가 1증가한다.

두 트리의 depth가 p>q이면 p가 q의 부모 노드가 되고, q>p이면 q가 p의 부모 노드가 된다.

merge된 간선은 답집합에 넣어준다.

그림 잘못된거입니당 여기 2-5 로 가는 간선이 1-4보다 먼저 추가 되어야해용 prim도!

Best/Worst Case Time Complexity Analysis

• basic operation: compare

• input size: n, m (numbers of vertexes and edges)

  • 이음선 정렬하는데 걸리는 시간 $\theta(m lg m)$

  • 반복문 안에서 걸리는 시간: 루프 m번 수행함 (equal, merge, find는 모두 상수의 복잡도)

    : m
    

  • initial에서 걸리는 시간: n

    ⇒ 간선의 수가 노드의 수보다 많으므로 결국 $\theta(m\ lg\ m)$

• 최선의 경우

  • 모든 정점이 모든 간선으로 다 연결되는 경우
  • 간선의 개수는 $\left (\frac{n (n + 1) }{2} \right)$ 이므로 $n^2$ 이 된다.
  • 따라서 $\theta(n^2\ lg\ n)$ 이 된다.

• find의 best case

  : find하는 노드들이 순차 탐색처럼 길게 늘여져 있을 때

  	![](https://velog.velcdn.com/images/byeoneunyoung/post/81195cf0-895c-4cfb-8a3f-76b24d8f4167/image.png)

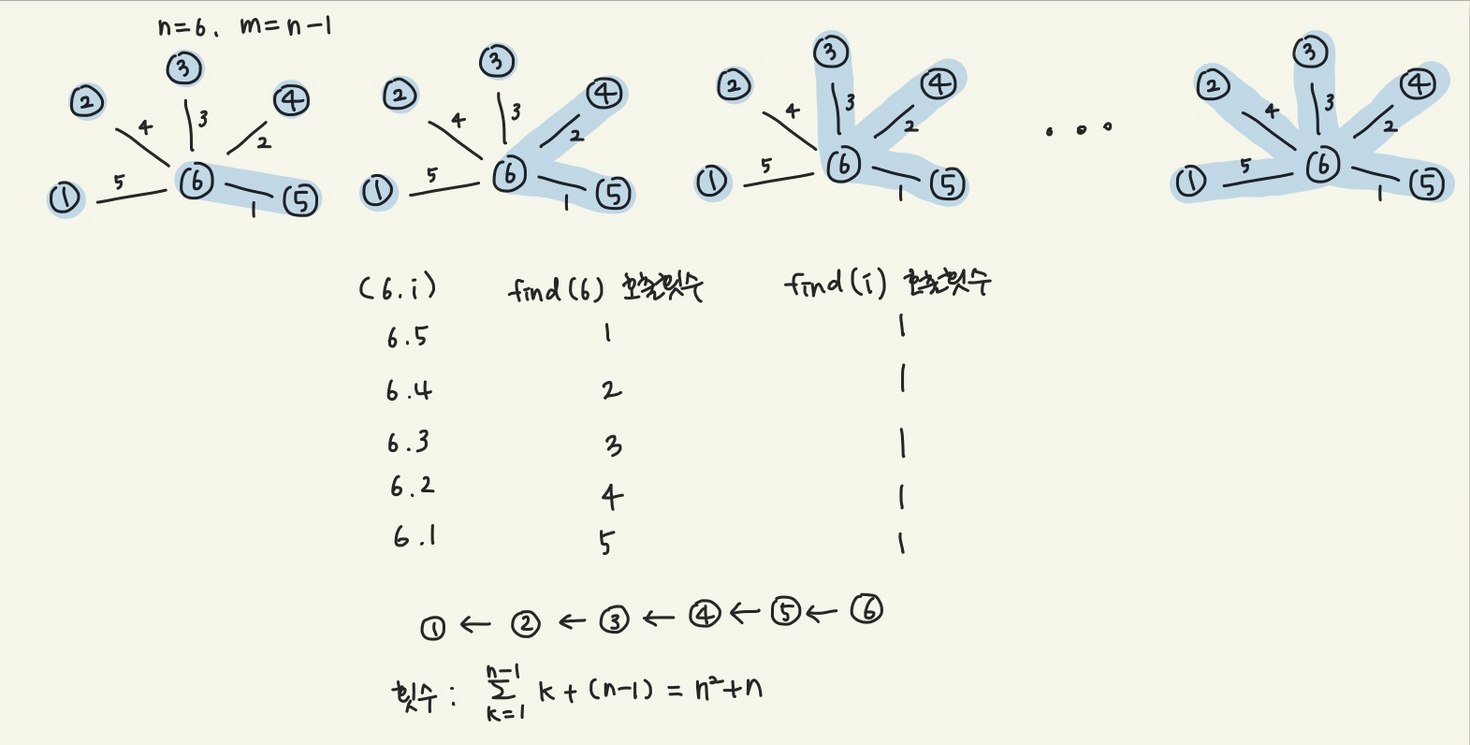  -최악일때 find함수 복잡도