Sum of Subsets Problem

Sum of Subset Problem이 뭔데?

양의 정수인 w와 양의 정수인 W가 주어진다.

⇒ 각 노드의 가중치인 w와 우리가 구해야하는 노드들의 합인 W가 주어진다.

이 알고리즘의 목표는 노드의 가중치의 합이 W가 되는 모든 subset을 찾는 것이다.

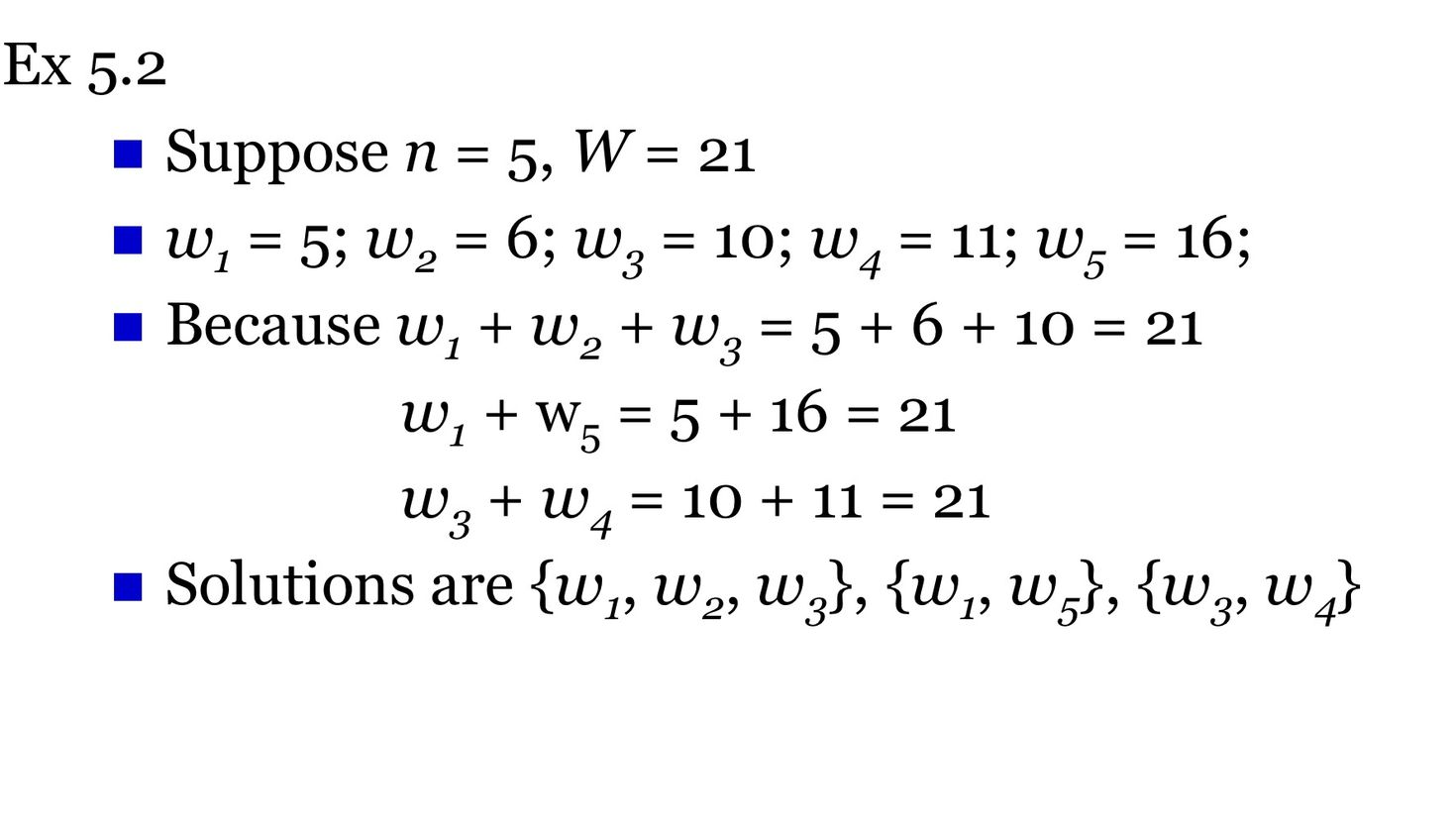
Sum of Subset 문제의 상태 공간 트리 구성

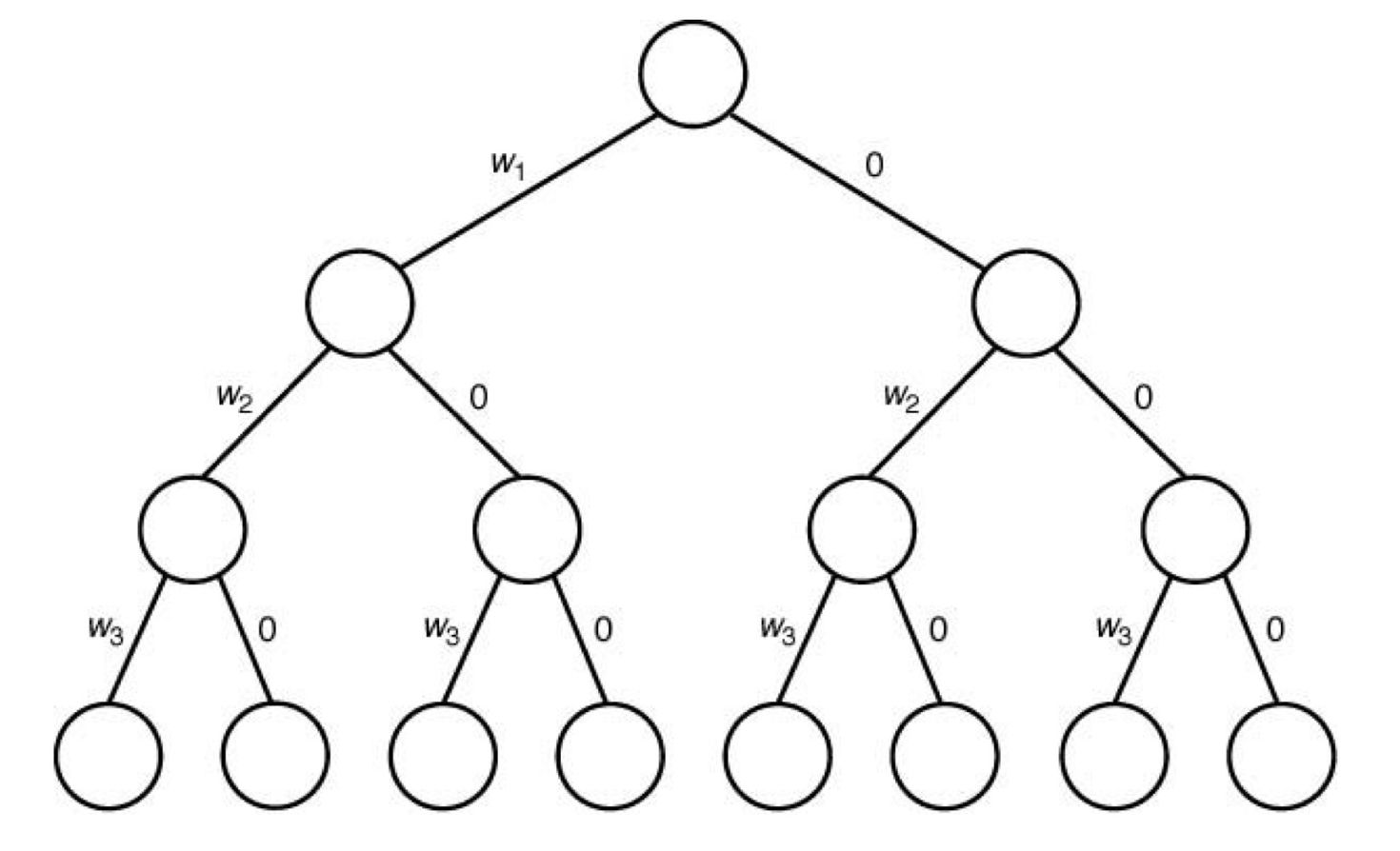
Backtracking 방식으로 해결하기

상태 공간 트리: State Space tree

1. n의 개수에 따라 depth가 정해짐
2. weight of node is sum of selected node
3. 답을 일찍 만나면 자식 노드는 만나지 않음

Promising(non-promising한 조건)

가중치를 오름차순으로 정렬

1. $weight$: $i$ 레벨의 가중치까지의 합

   $weight + w_{i+1} > W$ ⇒ non-promising

   현재까지의 합 + 다음 노드 > 구해야 하는 값

2. $total$: 남아있는 노드들의 합(현재 노드에서 최대로 더할 수 있는 가중치의 합)

   $weight + total < W$ ⇒ non-promising

   현재까지의 합 + 앞으로 얻을 수 있는 값 < 구해야 하는 값

   즉, 현재까지의 합에서 남아있는걸 더 더해봤자, 내가 원하는 값이 나오지 않으면 유망하지 않다.

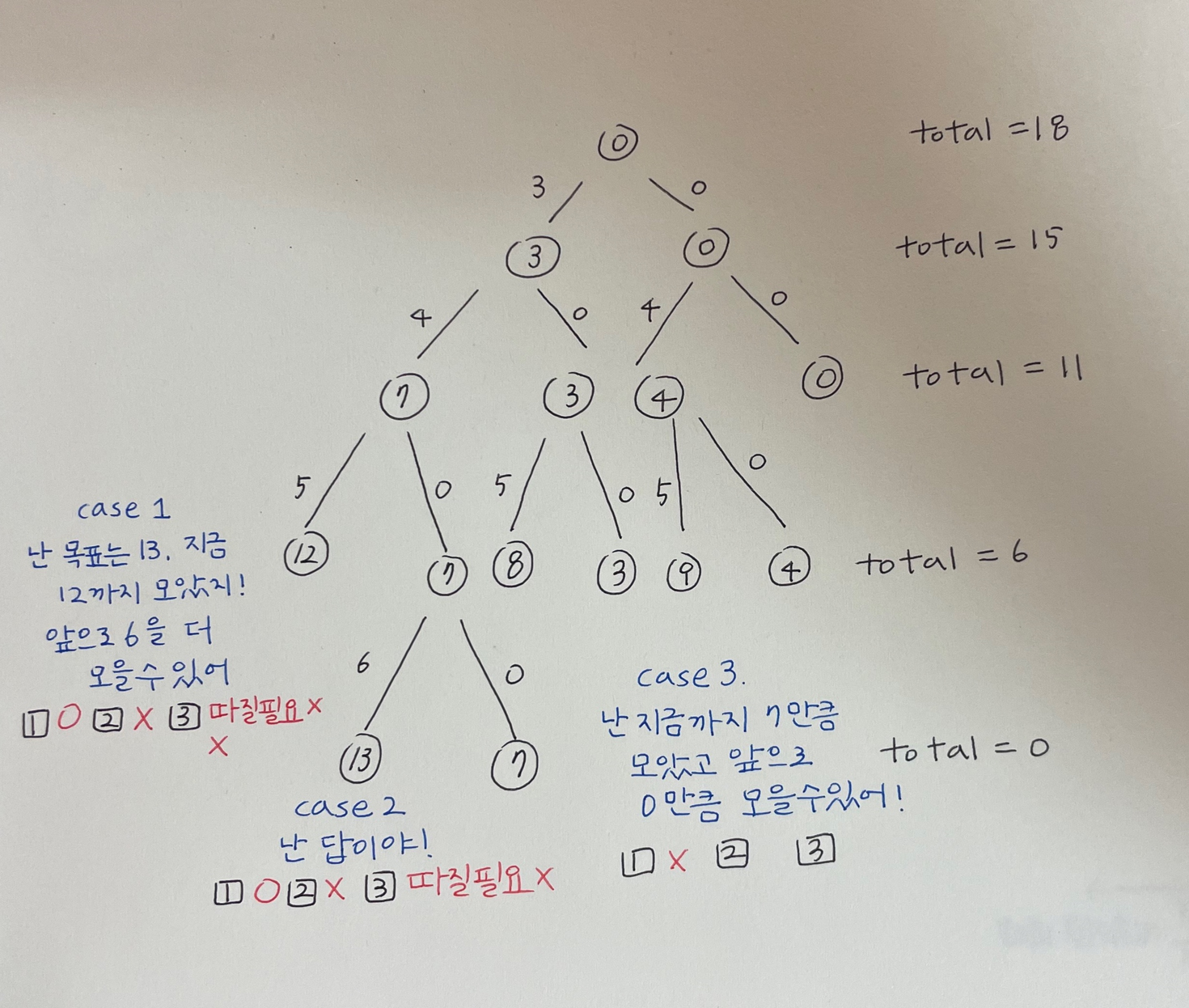
pseudo code

void sum_of_subsets( int i, int weight, int total)
{
		if(promising(i)){
				if(weight == W) cout<< include[1]~include[i];
				else{
						include[i+1] = "yes";
						sum_of_subsets(i+1, weight + w[i+1], total - w[i+1]);
						include[i+1] = "no";
						sum_of_subsets(i+1, weight, total - w[i+1]);
				}
}

bool promising(index i)
{
		return (weight + total > = w) 
					&& (weight == W || weight + w[i+1] <= W);
}

여기서 promising 함수의 리턴 조건문의 순서가 중요한 이유

1️⃣ weight + total ≥ W

먼저 답이 될 수 있는지를 체크한다. 만약에 더해질 수 있는 값이

구해야하는 값보다 크거나 같아야 답일 수 있기 때문이다.

2️⃣ (weight == W) || 3️⃣ (weight + w[i + 1] ≤ W)

만약, 2️⃣답이거나 3️⃣ 자식과 더했을 때 답보다 더 작은 값이거나 같으면

유망하므로 1을 리턴한다.

• 만약 순서가 3️⃣ || 2️⃣ && 1️⃣ 답이 leaf에서 먼저 나오면, w[i+1]을 참조할 수 없다. error가 발생 할 것
  

분석하기

최악의 상황 가정하기

: n개의 노드가 있을 때, 첫번째 노드에서 n-1번째 노드까지는 모두 더해서 W를 만족시키지 못하지만, 마지막 노드인 n번째 노드 == W일 때

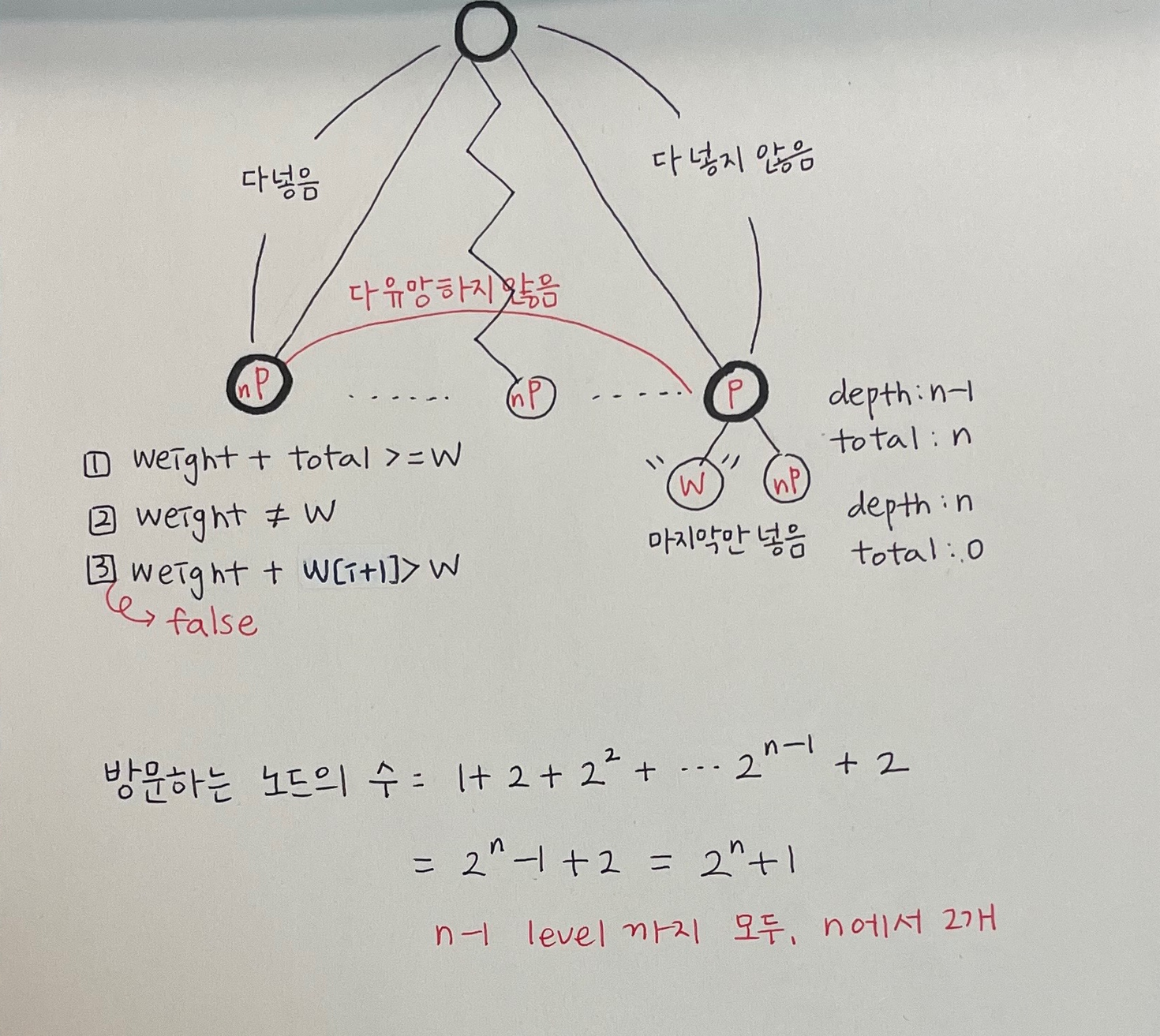
Sum of subset은 NP 문제이다.

지수 이상 걸리고, 다른 알고리즘 사용해도 지수보다 좋지 못하며, 그러한 알고리즘이 존재하지 않는다는 것을 증명한 사람도 없다.