Greedy approach

최적화 문제긴 하나, 재귀적이지 않다.

1. selection procedure(선정 과정)
2. Feasibility check
3. Solution check

눈에 보이는 것 중 가장 좋을 것 같은 답의 후보를 하나 고른다.

고른 하나가 답에 포함되는지, 조건을 설정하여 체크한다.

새로 얻은 해답 모음이 정답인지 확인하고 정답이 아니라면 다시 모으러 간다.

→ 한 문제에 대해(instance) 최적의 해를 내놓는다고 할지언정, 그것이 모든 문제를 해결하지는 못한다는 단점이 있음⇒ GLOBAL OPTIMAL이 아님

Prim’s algorithm

최소 비용 신장트리를 만드는 방법 중 하나로, 해답 집합에 있는 노드 중, 해답 집합에 없는 노드와 연결된 가중치가 가장 작은 간선을 골라 MST를 만드는 방법이다.

즉, 눈앞에서 가장 가까운 노드를 선택하는 방법

알고리즘에서 사용되는 식과 용어

• 인접행렬로 표현된 그래프
• nearest[2~n]와 distance[2~n]
  • nearest[i] : 해답 집합에 속한 정점중에서 $v_i$에서 가장 가까운 정점의 인덱스
  • distance[i] = $v_i$와 nearest[i]를 잇는 이음선의 가중치

algorithm 코드 및 이해

distance와 vnear과 W배열 활용하는 방법 머리에 박박 집어 넣기

답 집합인 F를 먼저 초기화 하고, nearest는 모두 $v_1$으로 초기화하고, distance는 $v_1$과 $v_i$를 잇는 간선의 가중치로 초기화 한다.

반복문은 초기화 할 때 F에 넣었던 $v_1$을 제외한 정점을 모두 해답 집합에 추가할 때까지 반복된다.

최소값은 일단 무한대로 초기화 한다.

각 정점에 대해 distance[i]를 검사하여 가장 가까이 있는 노드(vnear) 를 찾는다.

(현재 distace는 $v_1$을 기준으로 초기화 되어있기 때문에, $v_1$과 가장 가까운 노드를 찾을 수 있다.)

찾은 vnear를 해답 집합인 F에 추가한다. 찾은 노드는 다시 선택 못하도록 distance 값을 -1로 수정

답 집합이 아닌 각 i번째 노드에 대해서 W[i][vnear]<distance[i]보다 작으면 distance[i] = W[i][venar]로 갱신해주고 nearest[i] = vnear로 갱신해준다.

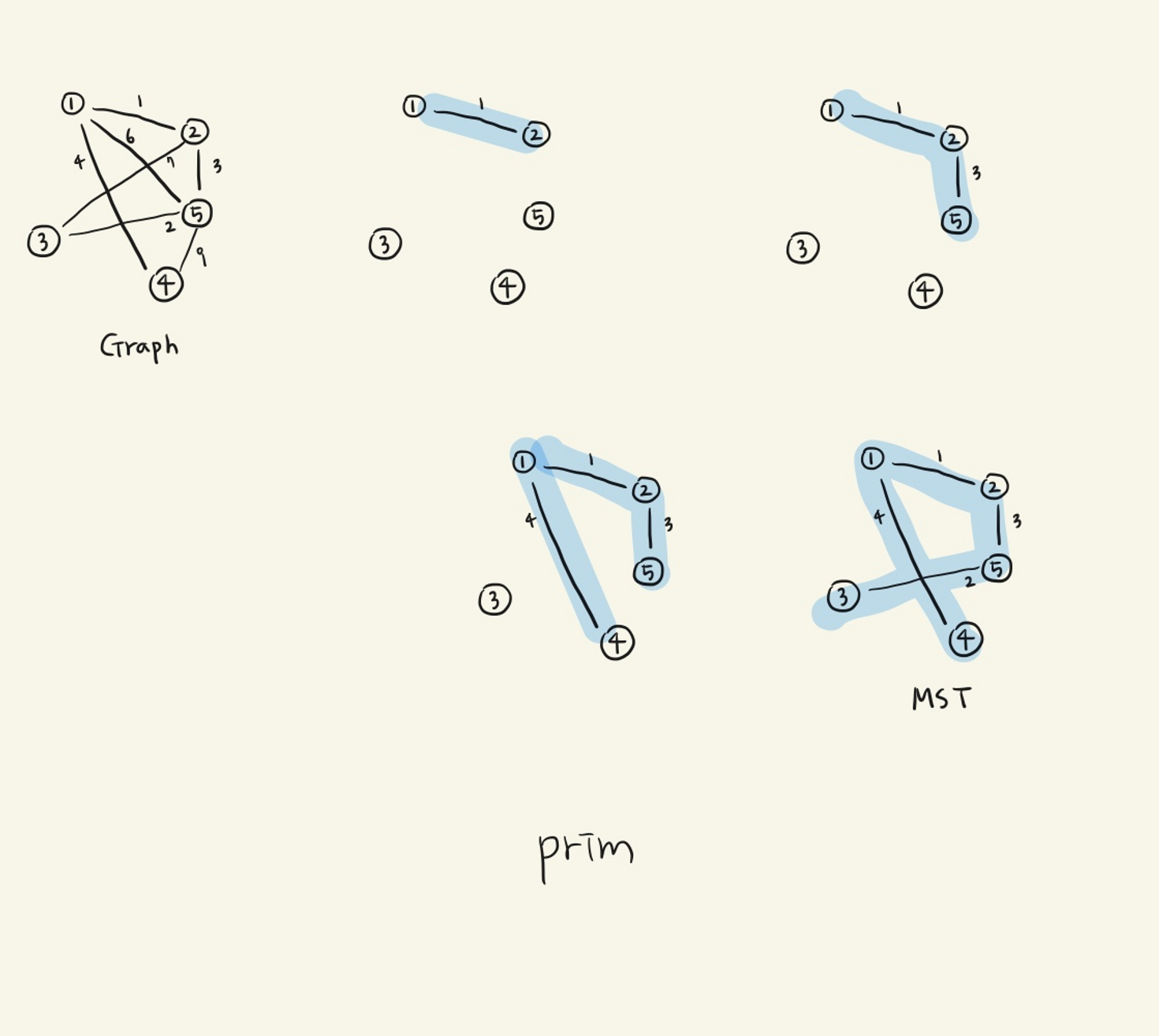
1-2 → 2-5 → 5-3 → 1-4 로 수정 필요!!!!

분석하기

• basic operation: repeat-loop안에 있는 반복문 2개
• input size: n(마디의 개수)
• 분석: repeat loop * (repeat loop 내의 반복문 횟수) (n-1)2(n-1) = $O(n^2)$
  

Optimality Proof(최적 여부의 검증)

prim알고리즘으로 찾아낸 트리가 진짜 최적인가?

• Definition 4.1
  • 비방향성 그래프 G = (V,E)가 주어지고 만약 E의 부분집합 F에 MST가 되도록 이음선을 추가할 수 있으면, F는 유망하다(promising)고 한다.
  • 즉, F가 우리가 찾는 MST가 될 수 있다는 뜻이다
• lemma 4.1
  • G = (V, E)는 연결된, 가중치 포함, 비 방향성 그래프라고 하고
  • F는 E의 유망한 부분 집합
  • Y는 F내의 간선에 의해 연결되어 있는 노드의 집합
  • 이때 Y안에 있는 정점과 V-Y에 있는 정점을 잇는 간선 중에서 가중치가 가장 작은 간선을 e 라고 하면 $F \bigcup {e}$ 는 유망하다. 왜? ⇒ F가 유망하기 때문에 최소 비용 신장 트리가 (V, F’)이면 F는 F’에 속한다. 최소라고 찾은 간선 e가 F’의 원소라면 F와 e를 합한 집합 역시 F’에 속한다. 즉, F는 최소비용 신장트리가 될 수 있는 유망주다! 근데 최소비용을 가진 간선 e가 F가 롤모델로 삼고 있는 F’의 구성요소라면! 당연히 F가 e를 흡수하면 F’처럼 되니까, F와 e를 합한 집합 역시 유망하다고 할 수 있는 것. 근데, e가 F’의 원소가 아니라면 F’와 e를 합한 집합은 반드시 cycle을 형성할 것이다. 이미 최소 비용 신장트리로 구성되어 있는 F’에다가 냅다 F’에 없는 간선인 e를 집어넣음 → 그러면 당연히 사이클이 일어날 수 밖에 없다.
    
• lemma의 검증
  • F가 유망하기 때문에 $F \subset F'$이면서 $(V, F')$가 MST가 되는 간선의 집합 $F'$가 반드시 존재
  • Case 1.
    • 만약 $e \in F'$ 라면 $F \bigcup \{e\} \subset F'$ 가 되고 $F \bigcup \{e\}$도 유망하다.
  • Case 2.
    • 만약 $e \notin F'$ 라면 $(V, F’)$는 신장 트리이기 때문에 $F’ \bigcup \{e\}$ 는 반드시 순환 경로를 하나 포함하게 되고, $e$는 반드시 그 순환 경로 가운데 한 간선이 된다.
      • Y에 있는 한 정점에서 V-Y에 있는 한 정점을 연결하는 어떤 다른 간선 $e’\in F’$ 가 그 순환 경로 안에 반드시 존재하게 된다. 그니까, 앞에 경우 설명하면서 F’가 순환 경로가 되었으니까 이미 F’에 있는 간선 중 하나는 무조건 순환 경로 안에 반드시 존재하게 된다.
        
      • 근데 $F’ \bigcup \{e\}$ 에서 e’를 제거해버리면 순환 경로가 사라지고 다시 신장 트리가 된다.
      • 여기서 e는 답으로 선택되지 않은 애들과 답으로 선택된 애들을 잇는 가장 가중치가 최소인 간선이기 때문에 e의 가중치는 e’보다 작거나 같아야 한다.
        • 왜냐하면 이미 F’는 최소 비용 신장 트리였다. 근데 우리가 임의로 e를 넣은 것이기 때문에 e’를 빼고 e를 넣으려면 e’와 e는 같은 값일 수 밖에 없을 것.
        • 최소만 선택했기 때문에 선택한 애들보다 더 작을 수 없다, 그럼 걔가 e’가 되어 먼저 F’에 들어 갔을 것이니까.
      • 그러면 $F’ \bigcup \{e\} - \{e’\}$는 MST이다.
      • 결론적으로 e’는 다시 F안에 절대로 속할 수 없다. F안의 간선은 답 집합 Y 안에 있는 정점들 만을 연결한다. → 유망한 애들이니까 Y로 선택된 애들만 연결 해야 함
      • 즉, $F \bigcup \{e\} \subset F’ \bigcup \{e\} - \{e’\}$가 되고 $F’ \bigcup \{e\}$는 유망하다
• Theorem 4.1
  • 정리: 프림의 알고리즘은 항상 최소 비용 신장 트리를 만들어 낸다.
  • 증명(수학적 귀납법)
    • 공집합은 당연히 유망
    • 주어진 반복이 이루어진 후 그때까지 선정하였던 간선의 집합인 F가 유망하다고 하면
    • $F \bigcup \{e\}$가 유망하다는 것을 보이면 된다
      • 여기서 e는 다음 단계의 반복 수행 시 선정된 간선이다.
      • 보조 정리 1에 의해 $F\bigcup\{e\}$는 유망하다고 할 수 있다.
      • 왜냐하면 간선 e는 Y에 있는 어떤 정점을 V-Y에 있는 어떤 정점으로 잇는 간선 중에서 최소의 가중치를 가지고 있기 때문이다.