The Traveling Salesperson Problem

외판원 문제

영업 사원이 고향에서 시작해서 각 도시를 한번씩 거쳐 다시 자신의 고향으로 돌아오는데 걸리는 최단 경로를 결정하는 알고리즘이다.

Brute Force로 풀면 안되는 이유

출발지를 빼고 각 노드를 한번씩 방문하는 경우의 수 이므로 Factorial의 가짓수가 나온다.

알고리즘에서 사용되는 용어 및 변수

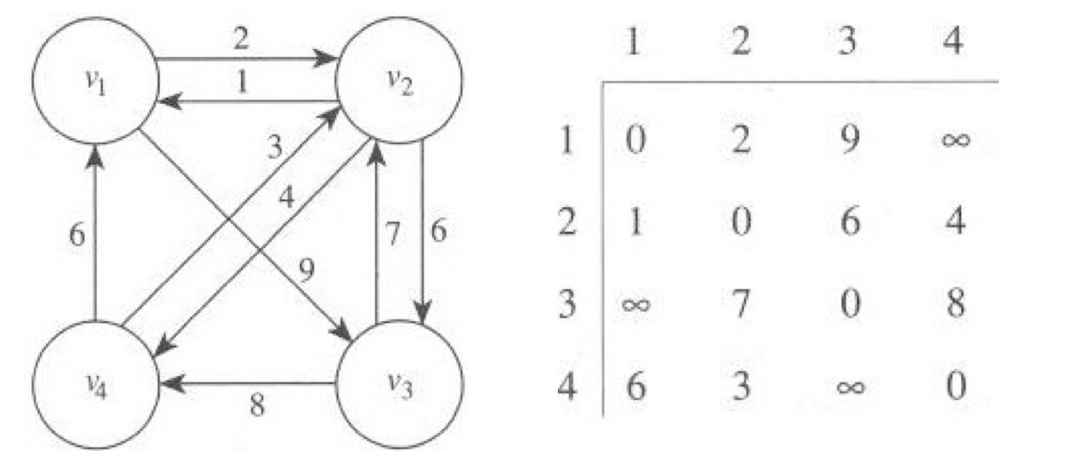
인접 행렬 W

• W[i][j] = i와 j를 연결하는 간선의 가중치, 없으면 inf로 나타냄
• W[i][i] = 0
  

set of vertices V

모든 간선들의 집합

A

V의 sub set

D[v][A]

$v_i$에서 $v_1$로 가는 최단 경로의 길이를 저장한 배열

각 간선은 A를 한번씩 다 거쳐 가야 한다.

• D의 의미를 예시로 설명해보자
  • V = {$v_1, v_2, v_3,v_4$} 은 노드들의 집합을 의미하고
  • [$v_1, v_2,v_3,v_4$] 경로를 나타내는 집합이다.
  • 만약 A가 {$v_3$}이라면 D$[v_2][\{v_3\}]$

점화식

첫번째 점화식은 i에서 j까지의 간선과, 집합 A에 있는 원소들 중 하나를 거쳐, A집합을 통해 $v_1$까지 가는 경우를 구하는 식이다. 반복문 내에서 변하는 값은 j와 $v_j$의 값이다.

두번째 점화식은 만약 A에 아무것도 없다면 그냥 $v_i$에서 $v_1$로 가는 경우와 같으므로, 두 노드를 연결한 간선의 가중치와 같다.

예제로 이해하기

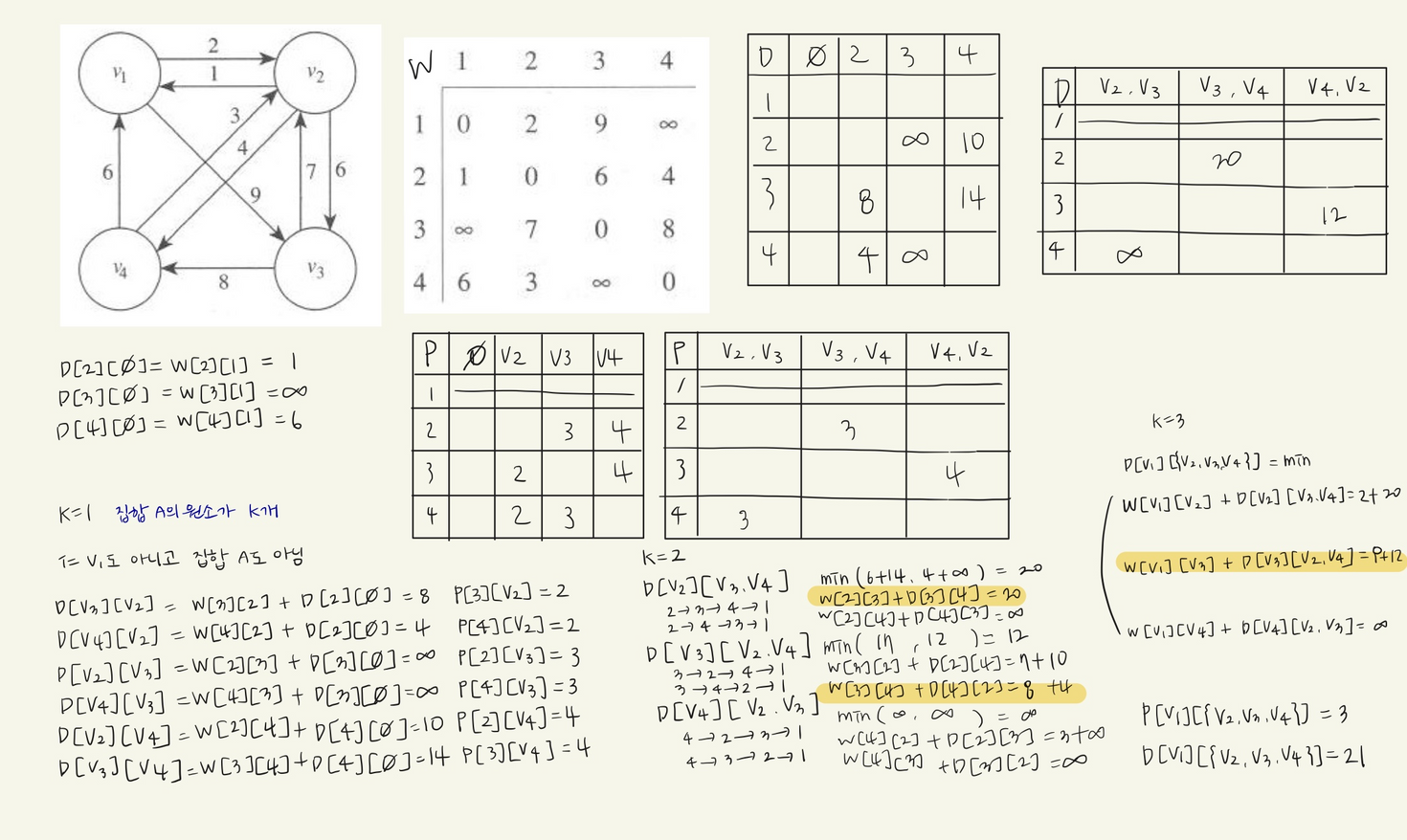
k는 집합 A의 원소의 개수, i는 v1도 아니고 집합 A도 아닌 원소

i가 변하면서, 집합 A도 같이 변화함.

배열 P와 D는 2개(원래 3개 필요하지만 마지막은 그냥 원소 하나라서 없어도 괜찮을 듯)

최소 값일 때의 j값을 P에 넣어주는 거

분석하기

시간 복잡도

• basic operation: 첫번째와 마지막 loop는 무시한 덧셈 연산
• input size: vertices의 개수 n

두번째와 세번째 값으로만 복잡도를 구하면

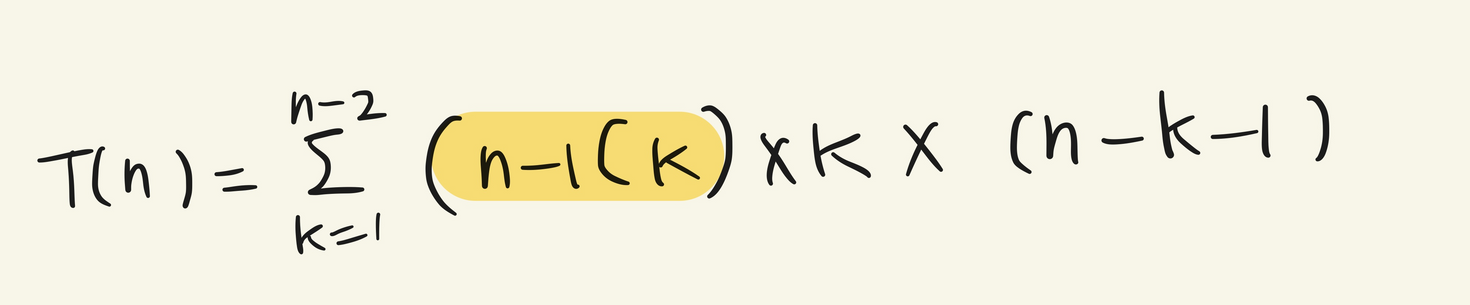
이러한 식을 쓸 수 있다. 이때

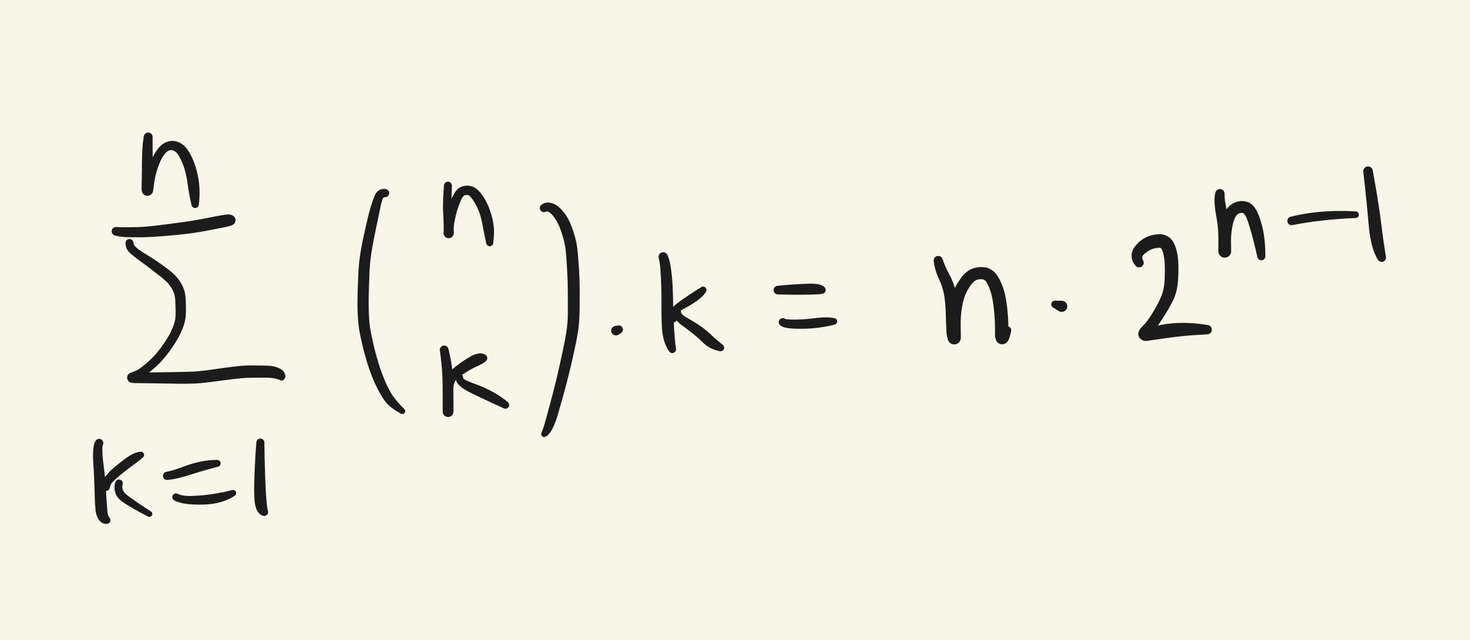
이러한 특성을 활용하기 위해 위의 식에서 노랗게 칠한 부분을 다음과 같이 바꿀 수 있다.

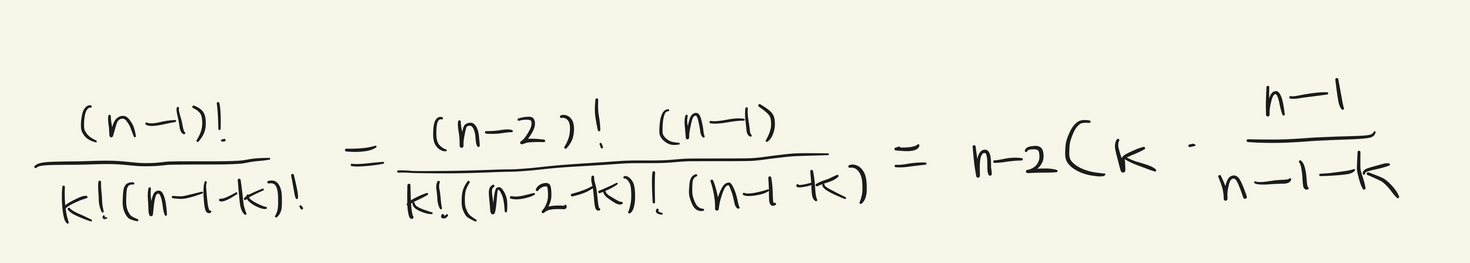
이를 적용하여 복잡도를 계산하면

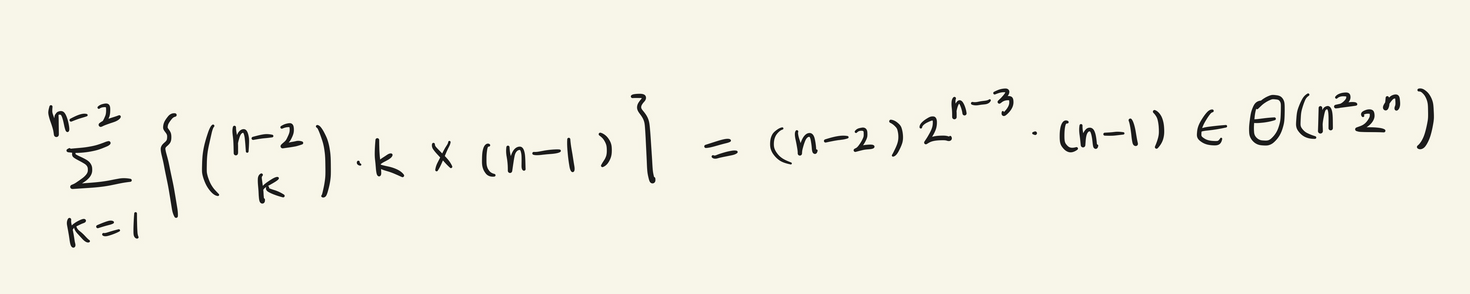
다음과 같은 식을 얻을 수 있다.

즉, 시간복잡도는 $\theta(n^22^n)$이다.

공간 복잡도

D배열과 P배열이 지배적으로 공간을 많이 차지하는데,

D and P배열의 두번째 항의 개수는
$V-v_i$의 n-1개의 노드 중에 k개를 선택하는 경우의 수 이므로 2^(n-1) 만큼의 공간이 필요하다.

그리고 첫번째 항의 개수는 최대 n개 이므로

$\theta(n2^n)$이다.