[Machine Learning] 미분 - Numerical, Partial Derivative

---

📚 수치 미분 (Numerical Derivative)

미분?
어떤 함수의 정의역 속 각 점에서 독립변수의 변화량과 함수값의 변화량의 비율. 그 비율의 극한 혹은 극한의 집합으로 치역이 구성되는 새로운 함수.

미분은 크게 두가지로 나눌 수 있다.

1. 해석 미분 : 미분 기본 공식을 이용해서 논리적으로 미분을 수행
2. 수치 미분 : 실제 수치값을 이용해 미분의 근사값을 얻어내는 방법

이때 파이썬에서는 실제 계산을 통해 미분의 근사치를 얻어내는 수치미분을 사용한다. 방법은 3가지로 전향차분, 후향차분, 중앙차분이 있는데 우리는 중앙차분을 통해 미분을 구현해 볼 것이다.

---

📚 중앙차분

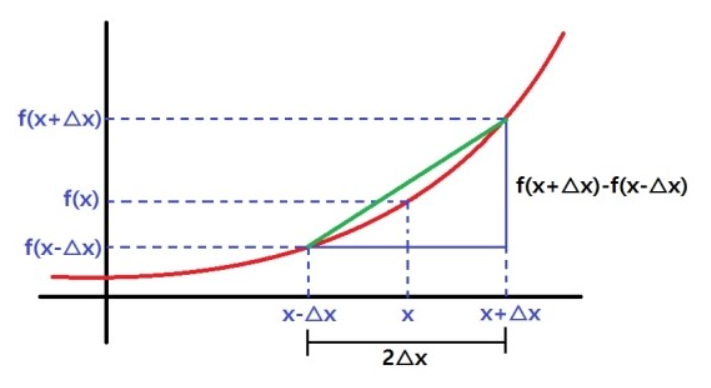
실제 미분과 가장 가까운 미분법으로, $x$에 $\pm \Delta x$를 해준 값을 사용하여 중앙 차분을 구한다. 이때 $\Delta x$의 값은 10$^{-8}$ 보다는 큰 값을 이용하며, 일반적으로 10$^{-6}$정도의 값을 사용한다.

중앙차분을 구하는 식은 다음과 같다.

이제 이를 코드로 구현해보자.

---

📚 Numerical Derivative 구현

def numerical_derivative(f, x):
    # 중앙차분을 이용한 미분값을 계산
    delta_x = 0.0001

    return (f(x + delta_x) - f(x - delta_x)) / (2 * delta_x)

# f(x) = x^2
def my_func(x):
    return x**2

result = numerical_derivative(my_func, 3)
print(result)

구현은 그렇게 어렵지 않은데, 중앙차분 공식을 그대로 코드로 작성하면 된다. 이때 주의해야 할 점으로 delta_x값인데, 이 값은 Hyper Parameter로, 값을 지정할 때 신경써야 할 부분이 있다.

---

📚 delta_x

delta_x
컴퓨터는 극한을 직접 계산할 수 없기 때문에 수치 미분에서는 delta_x를 매우 작은 값으로 설정하여 미분을 근사한다. 그러나 delta_x를 너무 작게 설정하면 반올림 오차가 발생하여 오히려 미분값이 부정확해질 수 있다.

그렇다면 delta_x 값을 어떻게 지정하면 좋을까?
=> 이때는 함수의 변화량에 따라 지정할 수 있다.

1. 변화량이 큰 경우 (ex. $y = \sin(1/x)$)
   

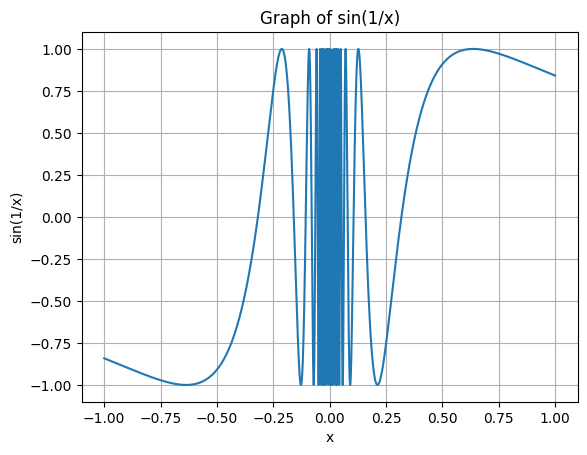
delta_x가 크면 두 점 사이의 기울기가 실제 순간 변화율과 크게 차이가 날 수 있으므로, delta_x를 작게 설정하여 두 점을 더 가깝게 만들어야 한다.

ex) $y = \sin(1/x)$

# 변화가 심한 함수 예시: f(x) = sin(1/x)
def f(x):
    return np.sin(1/x)
# 작은 delta_x 값 (예: 0.00001) 사용
delta_x = 0.00001
# x = 0.1 에서의 미분값 계산
x = 0.1
derivative = (f(x + delta_x) - f(x - delta_x)) / (2 * delta_x)
print(f"x = {x} 에서의 미분값: {derivative}")
# x = 0.1 에서의 미분값: 83.90713432193664

2. 변화량이 작은 경우 (ex. $y = x^2$)
   

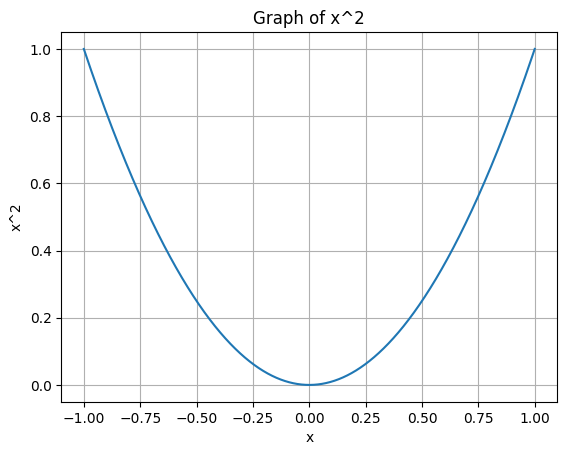
delta_x가 크더라도 두 점 사이의 기울기가 실제 순간 변화율과 크게 차이가 나지 않으므로, delta_x를 크게 설정해도 비교적 정확한 미분값을 얻을 수 있다.

ex) $y = x^2$

# 변화가 완만한 함수 예시: f(x) = x^2
def f(x):
    return x**2
# 큰 delta_x 값 (예: 0.01) 사용
delta_x = 0.01
# x = 2 에서의 미분값 계산
x = 2
derivative = (f(x + delta_x) - f(x - delta_x)) / (2 * delta_x)
print(f"x = {x} 에서의 미분값: {derivative}")
# x = 2 에서의 미분값: 3.999999999999937

그러면 delta_x를 함수에 따라 자동으로 설정할 순 없을까?
=> autograd 라이브러리를 사용하여 자동으로 미분을 진행할 수 있다.

import autograd.numpy as np
from autograd import grad

# 자동 미분을 위한 함수 정의
def f(x):
    return np.sin(1/x)

# 자동 미분 함수 생성
gradient = grad(f)

# x = 0.1 에서의 미분값 계산
x = 0.1
derivative = gradient(x)

print(f"x = {x} 에서의 미분값: {derivative}")
x = 0.1 에서의 미분값: 83.90715290764523

---

📚 편미분 (Partial Derivative)

편미분?
독립변수가 두 개 이상인 다변수 함수에서 미분을 할 때 사용하는 미분법

이와 같은 x, y 두 변수로 이루어진 함수 f가 있다고 하자.
이를 x와 y에 대해 각각 미분하면,

이와 같이 나타낼 수 있는데, 이를 편미분이라고 한다.
이제 이를 코드로 구현해보자.

---

📚 NumPy iter

def iter(x):
    it = np.nditer(x, flags=['multi_index'])

    while not it.finished:
        print(it.multi_index)

        it.iternext()

iter(np.array([[1, 5, 6, 4], [7, 6, 1, 2]]))
# (0, 0)
# (0, 1)
# (0, 2)
# (0, 3)
# (1, 0)
# (1, 1)
# (1, 2)
# (1, 3)

먼저 편미분을 쉽게 구현하기 위해 NumPy의 nditer 함수를 알아보자. nditer를 사용할 경우, 다양한 차원의 ndarray를 복잡한 for문이 필요없이 쉽게 요소를 탐색할 수 있다.

---

📚 Partial Derivative 구현

def partial_derivative(f, x):
    # f : 미분을 하려는 함수 (다변수 함수)
    # x : 모든 변수를 포함하고 있는 ndarray(차원 무관) ex) [1.0, 2.0]

    delta_x = 0.0001
    derivative_x = np.zeros(x.shape) # [0.0, 0.0]

    it = np.nditer(x, flags=['multi_index'])

    while not it.finished: # 첫번째 변수에대한 예시
        idx = it.multi_index # 1.0

        tmp = x[idx] # 첫번째 index에 대한 값을 임시로 저장 (1.0)

        x[idx] = tmp + delta_x # [1.0001, 2.0]
        fx_plus_delta = f(x) # f(x + delta_x)

        x[idx] = tmp - delta_x # [0.9999, 2.0]
        fx_minus_delta = f(x) # f(x - delta_x)

        derivative_x[idx] = (fx_plus_delta - fx_minus_delta) / (2 * delta_x)

        x[idx] = tmp # 원복
        
		# 이후 x의 다음 원소에 대해서 똑같이 반복
        it.iternext()

    return derivative_x

우선 중앙차분 공식을 사용하여 구현한 코드인데, iter를 사용하여 입력받은 원소 (여기선 독립변수의 개수)에 상관없이 동작이 가능하다. 각각의 원소마다 delta_x를 더한 값과 뺀 값을 구하여 중앙차분을 사용해 미분값을 구한 후 derivative_x에 저장하는 방식으로 동작한다.

구현한 코드를 통해 결과를 보자.

# 1변수 함수
def my_func1(x): # x^2
    return x**2

result1 = partial_derivative(my_func1, np.array([3.0]))
print(result1) # [6.]

# 2변수 함수
def my_func2(input_object): # 2x + 3xy + y^3
    x = input_object[0]
    y = input_object[1]
    return 2*x + 3*x*y + np.power(y, 3) 
    

result2 = partial_derivative(my_func2, np.array([1.0, 2.0]))
print(result2) # [ 8. 15.00000001]

# 3변수 함수
def my_func3(input_object): # 2xy + 3xy^2z + 7z^3
    x = input_object[0]
    y = input_object[1]
    z = input_object[2]
    return 2*x*z + 3*x*np.power(y, 2)*z + 7*np.power(z, 3)

result3 = partial_derivative(my_func3, np.array([[1.0], [2.0], [3.0]]))
print(result3)
# [[ 42.        ]
#  [ 36.        ]
#  [203.00000007]]

이때 다변수 함수를 작성할 때 전달하는 원소를 ndarray로 전달해 주면된다.

---