[Machine Learning] 단순 선형 회귀 - Simple Linear Regression 1

ByungJik_Oh·2025년 4월 1일

AI machine learning

[Hyundai Rotem KDT]

목록 보기

10/22

📚 Regression Analysis

Regression Analysis (회귀 분석)
회귀 분석이란 어떤 데이터에 대해 그 데이터에 영향을 주는 조건들의 영향력을 이용해서 데이터에 대한 조건부 평균을 구하는 방법이다.

다시 말해, 어떠한 데이터에 대해서 그 값에 영향을 주는 조건들의 평균적인 영향력을 이용해서 데이터를 가장 잘 표현하는 함수를 구하는 방법이다.

Rgression Analysis에는 다양한 방법이 있다.

단순 선형 회귀 (Simple Linear Regression) : 하나의 독립변수와 하나의 종속변수 간의 관계를 모델링한다. 일반적으로 직선의 형태로 나타낸다.
다중 선형 회귀 (Multiple Linear Regression) : 둘 이상의 독립변수와 하나의 종속변수 간의 관계를 모델링한다. 다양한 독립변수 간의 영향을 동시에 고려할 수 있다.
다항 회귀 (Polynomial Regression) : 독립변수와 종속변수 간의 비선형 관계를 모델링하는데 사용한다. 다항식을 사용하여 적합한 곡선을 형성한다.
로지스틱 회귀 (Logistic Regression) : 이진 분류 문제(두 개의 클래스로 예측하는 문제)에 사용된다. 선형 회귀와 이름은 비슷하지만, 종속변수가 이항 분포를 따르고, 로지스틱 함수를 사용하여 확률을 예측한다.
릿지 회귀 (Ridge Regression) : 다중 선형 회귀에서 사용되며, 과적합을 줄이기 위해 L2규제를 추가한 모델이다. 규제 항은 회귀 계수의 크기를 제한한다.
라쏘 회귀(Lasso Regression) : 다중 선형 회귀에서 사용되며, L1규제를 추가하여 회귀 계수를 0으로 만들어 변수 선택(Feature Selection)을 수행한다.
릿지 회귀와 라쏘 회귀의 조합 (Elastic Net Regression) : L2규제와 L1규제를 동시에 사용하여, 두 규제의 특성을 모두 갖는다.
시계열 회귀 (Time Series Regression) : 시간에 따라 변화하는 데이터에 대한 회귀 분석을 수행한다. 시계열 데이터의 특성을 고려하여 모델을 구성한다.

이번 글에선 Simple linear Regression에 대한 내용을 다뤄볼 것이다.

📚 Simple linear Regression

독립변수, 종속변수가 1개 있는 데이터에 대해 Simple linear Regression을 적용할 수 있다. 이때 독립변수 $x$ 가 1개인 경우 그 값에 영향을 주는 조건을 고려하여 함수식을 만든다면 아래와 같은 함수식이 만들어 질것이다.

y = \beta_0 + \beta_1x

여기서 독립변수 $x$ 에 영향을 주는 요인이 $\beta_1$ 이고 상수항을 $\beta_0$ 라고 표현하였다. 이는 또한

y = Wx + b

로도 나타낼 수 있으며 우리는 주어진 종속변수 $y$ 와 독립변수 $x$ 를 사용하여
$W$ (가중치)와 $b$ (절편)을 찾아 데이터를 가장 잘 나타내는 직선을 찾을 것이다.

이해를 위해 대략적으로 코드로 재현해보자.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

df = pd.DataFrame({
    '공부시간(x)' : [1, 2, 3, 4, 5, 7, 8, 10, 12, 13, 14, 15, 18, 20, 25, 28, 30],
    '시험성적(t)' : [5, 7, 20, 31, 40, 44, 46, 49, 60, 62, 70, 80, 85, 91, 92, 97, 98]
})

plt.scatter(df['공부시간(x)'], df['시험성적(t)'])
plt.plot(df['공부시간(x)'], df['공부시간(x)']* 5 - 7, color='g') # y = 5x - 7
plt.plot(df['공부시간(x)'], df['공부시간(x)']* 4 - 10, color='magenta') # y = 4x - 10
plt.plot(df['공부시간(x)'], df['공부시간(x)']* 2 + 3, color='r') # y = 2x + 3
plt.plot(df['공부시간(x)'], df['공부시간(x)']* 1 + 8, color='b') # y = x + 8

plt.show()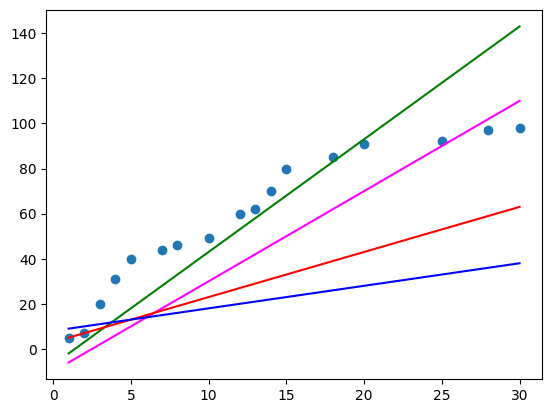

이렇게 임의로 1차 방정식을 이용해 데이터 scatter 위에 직선을 그렸는데 위 그림에서는 초록색 직선( $y = 5x - 7$ )이 가장 데이터와 가까워 보인다. 이러한 작업을 통해 데이터와 가장 가까운 직선을 찾는 것을 Regression 이라고 한다.

📚 구현 절차

코드를 구현하는 절차는 다음과 같이 나눠서 생각할 수 있다.

Training Data Set 준비 : Python의 list slicing 혹은 list comprehension 등을 이용하여 머신러닝의 입력으로 사용될 데이터를 NumPy array(ndarray) 형태로 준비한다.
Linear Regression Model 정의 : Weight와 bias를 정의한 후 이를 이용하여 우리가 완성할 Model을 정의한다.
loss function 정의 : 손실함수(loss function)를 코드로 작성한다. 이때 주의해야 할 점은 matrix 처리를 하기 위해 dot operation을 사용한다는 것이다.
learning rate 정의 : 일반적으로 customizing 되는 값으로 1e-4 정도로 설정하여 사용하고 loss 값을 보고 수치를 조절할 필요가 있다.
학습 진행 : 반복적으로 편미분을 통해 loss값이 최소가 되는 W와 b값을 update하는 처리를 구현해야 한다. 이때 이론상으론 loss값의 최소는 0이지만, 우리 모델의 loss값의 최소는 알 수 없기 때문에 적당한 반복을 이용하여 학습을 진행한다. 이때 반복수를 epochs라고 한다.

이제 코드로 구현해보자.

📚 Simple linear Regression 구현 (Python)

먼저 임의로 만든 간단한 데이터로 학습 과정을 살펴보자.

import numpy as np
import matplotlib.pyplot as plt

📚 Training Data Set 준비

# Training Data Set을 준비 => y = 2x + 1
x_data = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
t_data = np.array([3, 5, 7, 9, 11]).reshape(-1, 1)

먼저 간단한 $y = 2x + 1$ 직선에 대한 데이터를 준비하였다. 일반적인 경우엔 당연히 데이터 전처리 과정이 필수적이다.

📚 Linear Regression Model 정의

# Weight, Bias 정의
# W는 독립변수가 1개이기 때문에 1개의 값을 가지고
# 형태는 2차원 matrix가 되어야 하며 초기값은 랜덤하게 생성
W = np.random.rand(1, 1) # 0부터 1사이의 균등분포에서 실수를 생성 (1행 1열로 생성)
b = np.random.rand(1)

우선 초기의 W, b의 값은 랜덤하게 지정한다. 이를 통해 초기 무작위 값이 들어있는 W, b가 학습 과정을 통해 데이터를 잘 나타내는 값으로 근사되는지 확인해보자.

📚 loss function 정의

# 평균 제곱 오차(MSE)를 사용해서 loss를 구한다.
def loss_func(input_obj): # input_obj : [W, b]
    
    input_W = input_obj[0].reshape(-1, 1)
    input_b = input_obj[1].reshape(-1, 1)

    y = np.dot(x_data, input_W) + input_b

    return np.mean(np.power(t_data - y, 2))

다양한 loss 함수에 대해선 추후에 다룰 예정인데, 현재 사용하는 loss 함수는 평균 제곱 오차(MSE)를 사용하는 함수이다.

간략하게 설명하자면,

평균 제곱 오차 (MSE)
평균 제곱 오차 (MSE)는 예측값과 실제값의 차이를 제곱한 후 평균을 구한 값이다. 다시 말해, 모델이 구한 직선과 각각의 데이터의 거리의 평균을 말한다.

이는 아래와 같이 나타낼 수 있다.

MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2

📚 learning rate 값 정의

learning_rate = 1e-4

learning rate는 Hyper parameter로, loss 값을 확인하며 적절한 learning rate를 지정해주어야 한다.

📚 학습 진행

def numerical_derivative(f, x):
    delta_x = 0.0001
    derivative_x = np.zeros(x.shape)

    it = np.nditer(x, flags=['multi_index'])

    while not it.finished:
        idx = it.multi_index

        tmp = x[idx]

        x[idx] = tmp + delta_x
        fx_plus_delta = f(x)

        x[idx] = tmp - delta_x
        fx_minus_delta = f(x)

        derivative_x[idx] = (fx_plus_delta - fx_minus_delta) / (2 * delta_x)

        x[idx] = tmp

        it.iternext()

    return derivative_x

먼저, learning rate와 편미분을 통해 loss값이 최소가 되는 W와 b값을 update하기 위해 편미분을 코드로 구현한다. 편미분에 대한 자세한 설명은 이전 글에 있다.

이제 학습을 진행시켜 보자.

# 준비된 구성요소들을 이용해서 로직을 실행
# 반복적으로 학습을 진행한다.
# epoch도 hyper parameter
for step in range(300000): # epochs = 300000

    # 편미분을 진행할건데 대상이 되는 함수는 loss함수이다.
    # 미분을 수행할 W 값과 b 값을 인자로 미분을 수행해야 한다.
    # ravel() : 2차원 이상의 ndarray를 1차원으로 변환해준다.
    input_param = np.concatenate((W.ravel(), b.ravel()), axis=0) # -> [W b]

    derivative_result = learning_rate * numerical_derivative(loss_func, input_param)

    W = W - derivative_result[0].reshape(-1, 1) # 개선된 W를 구할 수 있다.
    b = b - derivative_result[1].reshape(-1, 1) # 개선된 b를 구할 수 있다.

    if step % 30000 == 0:
        print(f'현재의 W, b 값은 : {W}, {b}, {step}')
        # 현재의 W, b 값은 : [[0.15304435]], [[0.74022404]] 30000
		# 현재의 W, b 값은 : [[1.97650897]], [[1.08481008]] 60000
		# 현재의 W, b 값은 : [[1.99148088]], [[1.03075672]] 90000
		# 현재의 W, b 값은 : [[1.99691051]], [[1.01115405]] 120000
		# 현재의 W, b 값은 : [[1.99887958]], [[1.00404506]] 150000
		# 현재의 W, b 값은 : [[1.99959368]], [[1.00146696]] 180000
		# 현재의 W, b 값은 : [[1.99985264]], [[1.000532]]   210000
		# 현재의 W, b 값은 : [[1.99994656]], [[1.00019293]] 240000
		# 현재의 W, b 값은 : [[1.99998062]], [[1.00006997]] 270000
		# 현재의 W, b 값은 : [[1.99999297]], [[1.00002537]] 300000

이와 같이 loss 함수에 learning rate를 곱한 값을 이용하여 주어진 epochs 동안 W와 b를 최적화한다. 이때 이러한 과정을 경사하강법이라고 하는데, 이 역시 추후에 다루겠다. 학습을 진행하면서 W와 b 값을 출력해보면, 점점 W = 2, b = 1에 가까워 지는 것을 확인 할 수 있다.

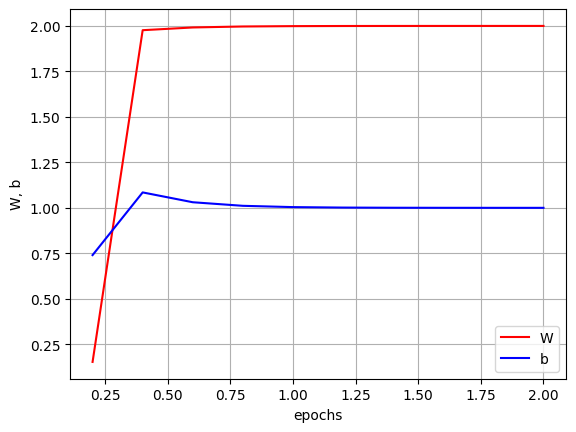
그래프로 직관적으로 확인해 볼 수 있다.

📚 예측

def predict(x):
    y = np.dot(x, W) + b
    return y
    
predict_result = predict(np.array([[7]]))
print(predict_result) # [[14.99999042]]

7에 대하여 값을 예측해보면 15 (2 x 7 + 1)에 근사한 값을 잘 도출해내는 것을 확인할 수 있다.

📚 실제 Data Set으로 학습

Ozone Data Set을 사용하여 코드를 전체적으로 확인하고, 직접 만든 코드와 sklearn library를 사용하여 만든 코드를 비교해보자. 이때 온도 변화량에 따른 Ozone량을 알아볼 것이기 때문에 독립변수는 Temp이고 종속변수는 Ozone이다. 여기선 결치값만 처리하였다.

Ozone Data의 분포는 다음과 같다.

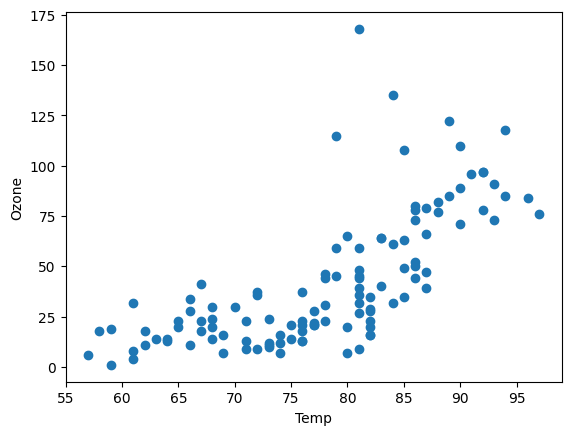
📚 python으로 구현

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# Raw Data Loading
ozone = pd.read_csv('/파일경로/ozone.csv')
df = ozone[['Temp', 'Ozone']]

# 데이터 전처리를 진행 => 결측치만 처리
new_df = df.dropna(inplace=False, how='any')

# Training Data Set 준비
x_data = new_df['Temp'].values.reshape(-1, 1)
t_data = new_df['Ozone'].values.reshape(-1, 1)

# Weight, Bias 정의
W = np.random.rand(1, 1)
b = np.random.rand(1)

# 수치 미분 함수
def numerical_derivative(f, x):
    delta_x = 0.0001
    derivative_x = np.zeros(x.shape)

    it = np.nditer(x, flags=['multi_index'])

    while not it.finished:
        idx = it.multi_index

        tmp = x[idx]

        x[idx] = tmp + delta_x
        fx_plus_delta = f(x)

        x[idx] = tmp - delta_x
        fx_minus_delta = f(x)

        derivative_x[idx] = (fx_plus_delta - fx_minus_delta) / (2 * delta_x)

        x[idx] = tmp

        it.iternext()

    return derivative_x

def loss_func(input_obj): # input_obj : [W, b]

    input_W = input_obj[0].reshape(-1, 1)
    input_b = input_obj[1].reshape(-1, 1)

    y = np.dot(x_data, input_W) + input_b

    return np.mean(np.power(t_data - y, 2))

# learning_rate 값 정의
learning_rate = 1e-4

# 학습 진행
# epoch도 hyper parameter
for step in range(300000):

    input_param = np.concatenate((W.ravel(), b.ravel()), axis=0) # -> [W b]

    derivative_result = learning_rate * numerical_derivative(loss_func, input_param)

    W = W - derivative_result[0].reshape(-1, 1)
    b = b - derivative_result[1].reshape(-1, 1)

코드의 전체적인 모습은 다음과 같다.

# 예측 함수
def predict(x):
    y = np.dot(x, W) + b
    return y
    
predict_result = predict(np.array([[75]]))
print(predict_result) # [[38.29475317]]

온도가 75도 일때 오존량은 38.29475317로 도출되었다.

📚 sklearn으로 구현

직전에 Python으로 구현한 모델을 간단하게 검증해 보기위해 같은 Data Set으로 sklearn을 사용하여 만든 모델과 비교해 볼 것이다.

왜 sklearn과 비교하는가?
간단한 Regression의 경우 sklearn library에서 자체적으로 데이터 전처리 및 최적의 Hyper parameter로 학습을 진행하기 때문에 sklearn으로 정답에 근사한 모델을 구현할 수 있기 때문이다.

from sklearn import linear_model

# model 생성
sklearn_model = linear_model.LinearRegression()

# 데이터를 이용하여 모델 학습
sklearn_model.fit(x_data, t_data)

# 모델을 완성했다는 것은 W와 b를 구했다는 의미이다.
print(f'W의 값은 : {sklearn_model.coef_}, b의 값은 {sklearn_model.intercept_}')
# W의 값은 : [[2.4287033]], b의 값은 [-146.99549097]

# 75도에 대한 예측 오존량
print(sklearn_model.predict(np.array([[75]]))) # [[35.15725689]]

sklearn으로 모델을 구현하였을 때, coef_(W)와 intercept_(b)를 사용하여 W와 b값을 알 수 있다.

📚 차이 확인

각 모델이 만든 직선을 그림으로 출력하여 차이를 직관적으로 확인해보자.
빨간색 직선은 Python 모델, 초록색 직선은 sklearn 모델이다.

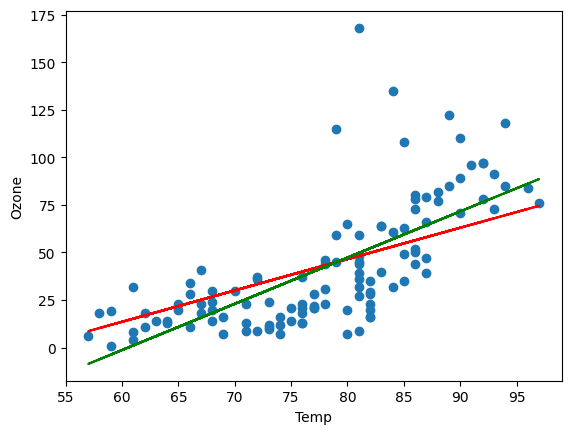
Python 모델 예측값은 38.29475317인 반면 sklearn 모델의 예측값은 35.15725689으로 차이가 있는 것을 확인할 수 있다. 이는 Python 모델을 구현할 때 데이터 전처리가 충분히 이루어지지 않았기 때문인데, 이것으로 데이터 전처리의 중요성을 볼 수 있다.