[AIAS] 3. Supervised Learning

본 내용은 인하대학교 정보통신공학과 홍성은 교수님의 인공지능응용 강의내용을 기반으로 작성한 내용입니다.

Regression vs Classification

• 회귀(Regression) : 연속적인 값을 예측한다.
• 분류(Classification) : 이산적인 값을 예측한다.
  - 이진 분류 : 0 또는 1로 예측
  - 다중 분류 : n개의 클래스로 예측

Model Parameters vs Hyperparameters

• Model Parameters : 학습을 통해 정해지는 값
• Hyperparameters : 사용자가 정의하는 값

Loss Function & Optimization

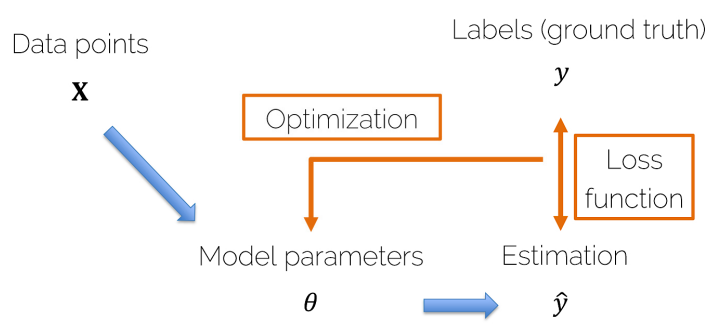
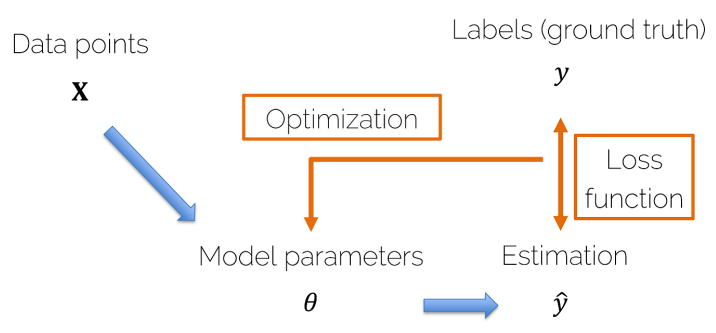
• 모델을 통해 예측된 target ^y가 생성된다.
• Loss Function : 하나의 input data에 대해서 오차를 계산하는 함수
• Loss Function(손실함수)을 통해 ^y와 y의 차이를 산출하고 이를 줄일 수 있는 파라미터를 반복적으로 구하는 과정을 Optimization(최적화)라고 한다
  * Cost Function : 모든 input dataset에 대해서 오차를 계산하는 함수

Linear Regression

• 지도학습은 크게 분류와 회귀로 구분된다.
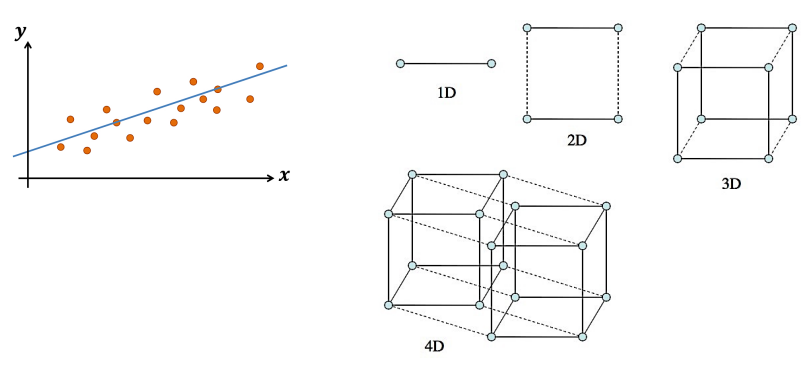
• 주어진 input x를 통해 target y를 설명하는 선형 모델을 찾는다.
• 2차원에서는 선으로, 3차원에서는 면으로 모델을 찾는다.
  
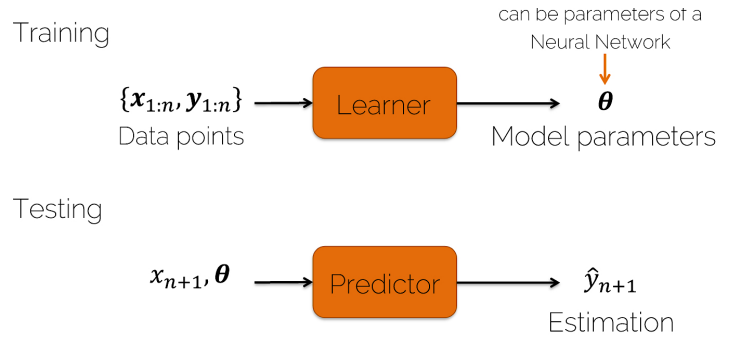
• Training을 통해 파라미터를 찾고, Test 과정에서 파라미터를 활용해 target y를 찾는다.
  
• 선형 모델은 다음과 같은 Weighted Sum 형태이다.
  

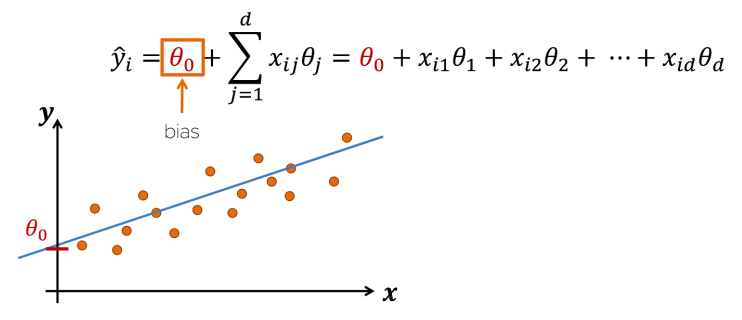
Loss Function & Optimization (in Linear Regression)

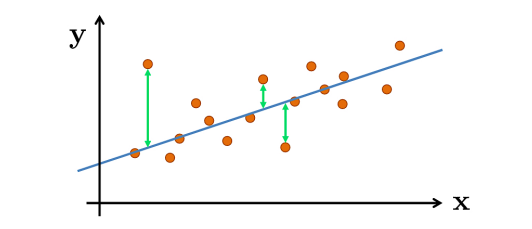
• 모델을 통해 계산된 선과 각 데이터 사이의 거리의 평균
• Loss는 최소화되어야 한다.
  
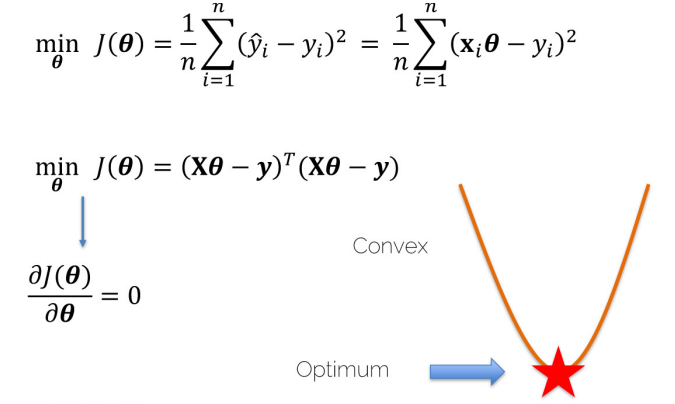
• Loss가 최소인 값을 구하기 위해서 Loss Function의 미분 값이 0인 점을 찾는다.

Logistic Regression

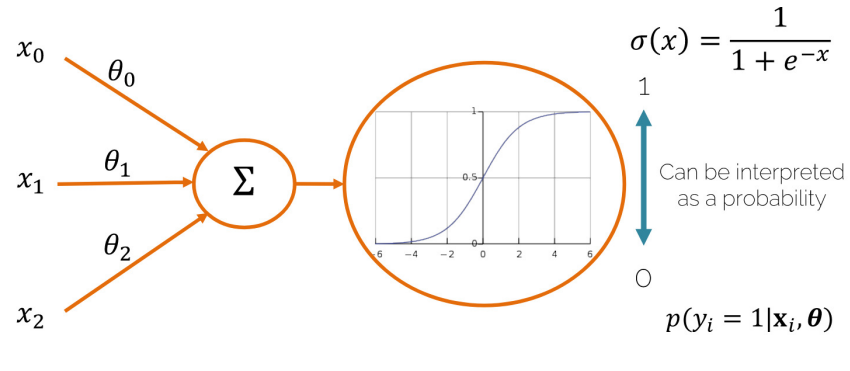
• Sigmoid(시그모이드) : 모든 값을 0과 1사이의 값으로 변환한다.
• Sigmoid 함수를 통해 회귀식의 결과를 0~1사이의 값으로 변환하고, 이를 이진 분류에 활용할 수 있다.

Loss Function & Optimization (in Logistic Regression)

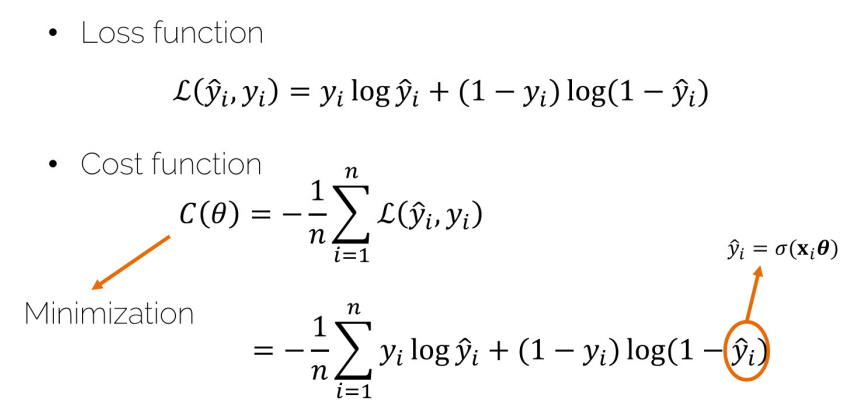
Linear Classifier

• f(x,W)를 통해 x에 대한 target score를 산출
• label에 맞는 target score를 향상시키는 Weight를 찾는 것이 목표

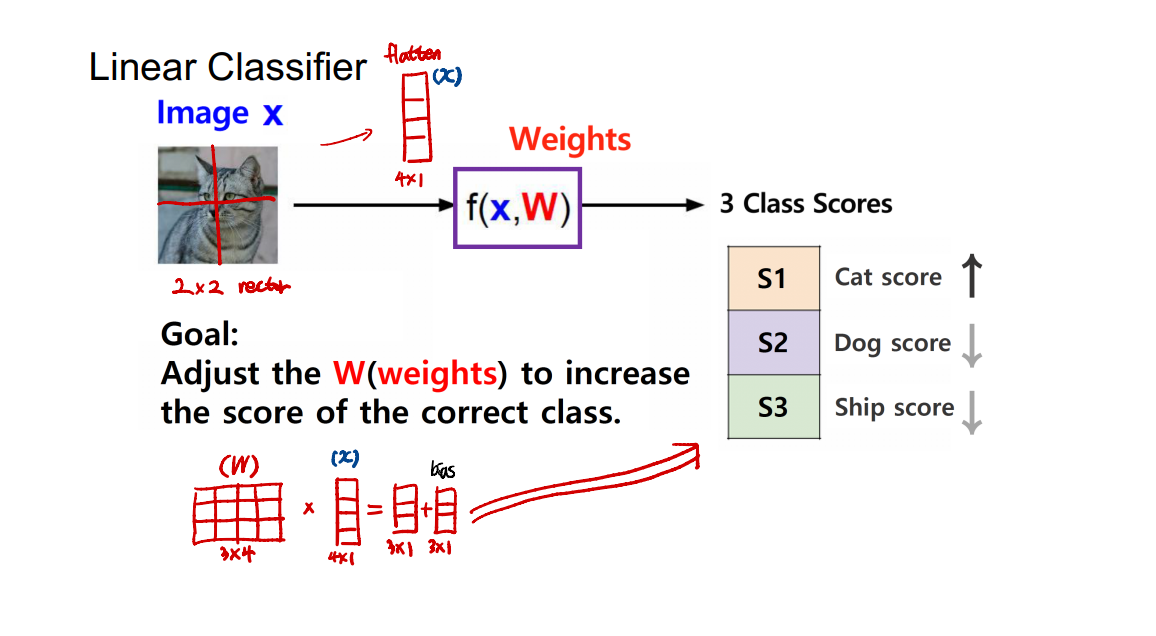
• 더 나아가 Target Score를 설정하여 그 차이를 구하는 Loss Function을 활용한다.
• Loss Function을 줄이는 W를 찾는 것이 목표
  

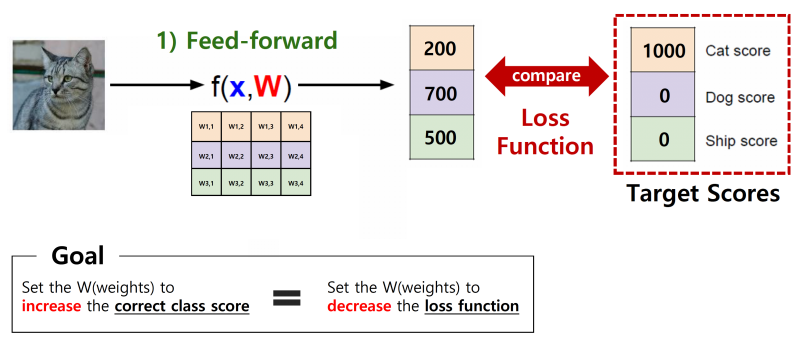
SVM Classifier

• 3가지 class를 분류하는 모델이며, f(x,W)를 통해 위와 같은 이미지에 대한 score를 산출한 모습이다.
  

★ Loss Function

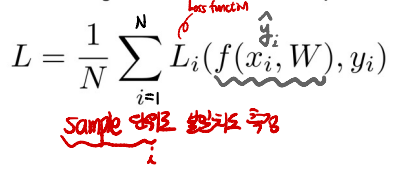
• sample 단위로 불일치도를 측정하여 전체 Loss Function을 계산한다.
• SVM에서 sample 단위의 Loss Function을 계산하는 방법은 아래와 같다.

정답O와 정답X의 차이가 k보다 작으면(정답O가 정답X+k 보다 더 크면) loss=0이다.(k는 하이퍼 파라미터)

• max(0, 정답X1 - 정답O + k)

• max(0, 정답X2 - 정답O + k)

• ...

• 위 값들을 더해준 값이 각 이미지의 Loss가 된다.
  

• max(0, 5.1-3.2+1) + max(0, -1.7-3.2+1) = 2.9

• max(0, 1.3-4.9+1) + max(0, 2.0-4.9+1) = 0

• max(0, 2.2-(-3.1)+1) + max(0, 2.5-(-3.1)+1) = 12.9

• 위 3개의 Loss의 평균 = 5.27

• 아래 문제 풀어보기
  

• Q1. 이 training 예제에서 Car score가 0.5 감소하면 손실은 어떻게 됩니까?

• Q2. 각 이미지 별 가능한 최소/최대 SVM 손실 L은 얼마입니까?

• Q3. 초기 score는 모두 0에 가까운 작은 값이라 할 때, N개의 예제와 C 클래스를 가정할 때 손실 L은 얼마입니까?
  

Linear vs SVM

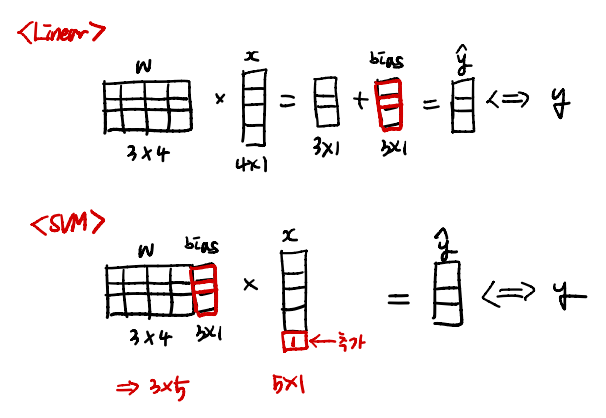
• 두 모델의 연산 결과는 같으나, SVM은 곱하기 하나로 target y를 구할 수 있으므로 연산 과정이 줄어든다.

Softmax Classifier

• 다중 분류에서 계산된 Score 값의 크기를 고려하여 합이 1이 되도록 변환해준다.

• ① y = exp(x) → 값의 양수화 + 큰 값은 더 커지고, 작은 값은 더 작아진다.
  

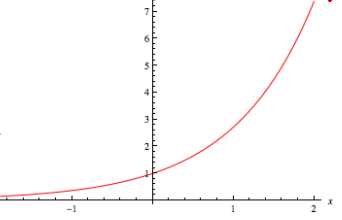
• ② Normalize : Sum to 1
  - logits : input x가 수많은 Weight층을 거쳐서 나오는 값(raw score)
  - logits을 확률값으로 변환한다.
  

Loss Function

• Softmax에서는 주로 Cross-entropy라는 Loss Function을 사용한다. Cross-entropy는 바로 아래에서 설명한다.
  

Cross-entropy

Information Theory

• 정보이론은 Cross-entropy의 전제 조건이다.
  
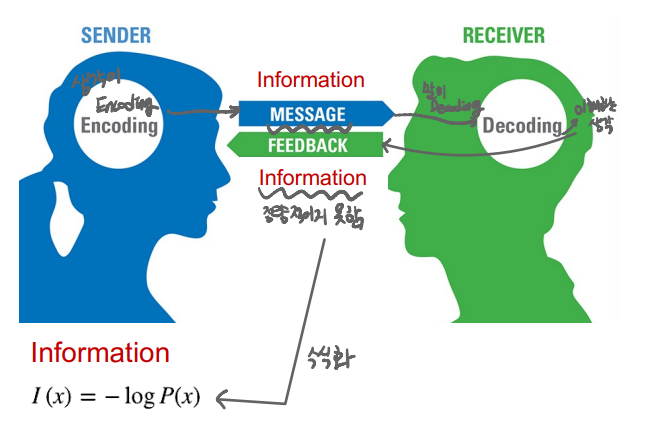
• 사람과 사람 사이에서 정보를 주고 받을 때, 정보를 보내는 사람은 생각(정보)를 메세지로 표현하는 Encoding을, 받는 사람은 메세지를 생각으로 변환하는 Decoding을 한다.
• 이러한 정보는 Encoding과 Decoding을 거치면서 완벽하게 일치하는 정보를 공유할 수 없으며, 내가 얻은 정보에 대한 불확실성이 존재한다.
• 주고 받는 정보를 정량적으로 표현하면 정보 I(x) = -logP(x)과 같다. 여기서 x를 sofmax를 거치고 난 뒤의 확률이라고 하자.
  
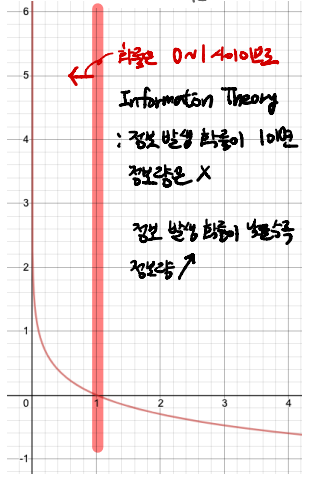
• 정보 발생 확률이 1이면 확실한 값이기 때문에 이로 인해 얻을 수 있는 정보량은 존재하지 않는다.
• 정보 발생 확률이 낮을수록 정보량은 높아진다.

(Shannon) Entropy vs Cross Entropy

• Entropy : 불확실성, 무질서도, 값을 예측하기 힘든 정도

• 동전 던지기를 생각해보자. 앞면과 뒷면이 나올 확률이 반반이지만, 항상 50%의 확률이 아니기 때문에 값을 예측하기 힘들다.

• 주사위 던지기를 생각해보면, 동전 던지기보다 값을 예측하기 더 힘들다. 이 때 주사위 던지기의 Entropy가 더 크다고 할 수 있다. 계산 식은 아래와 같다.
  

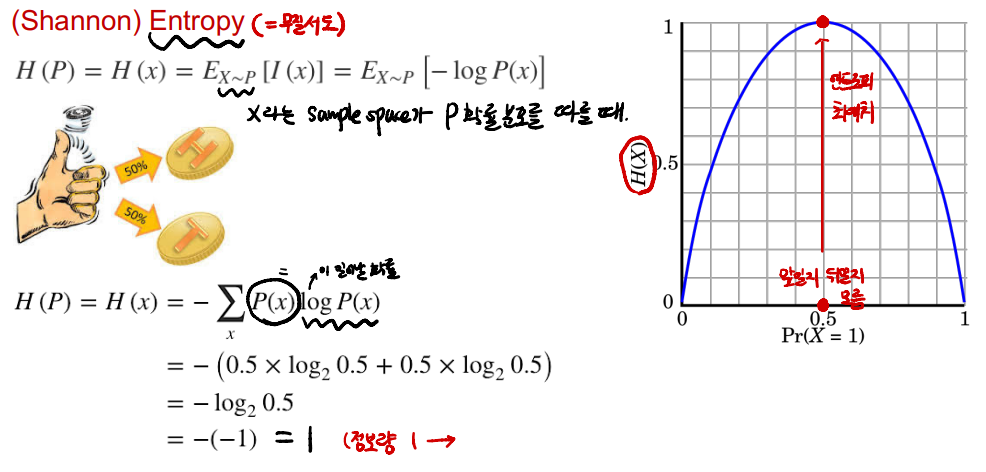
• Cross Entropy는 두 확률 분포를 모두 고려하여 확률 분포의 차이를 산출한다.
  

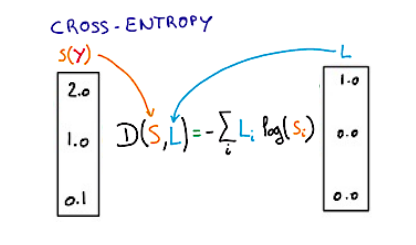
• ★ 불일치 척도를 계산하는 3가지 방법이 있다.
  

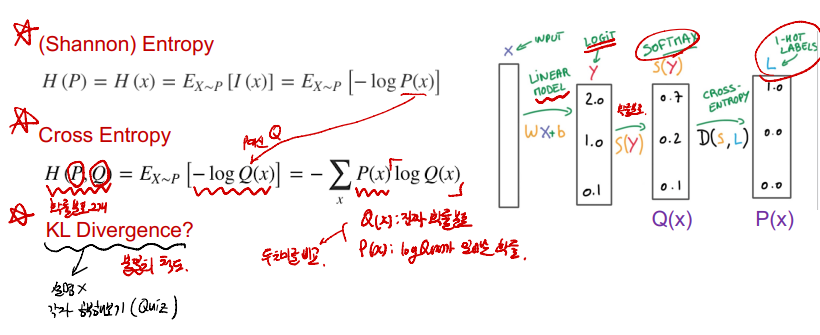
• KL Divergence(쿨백-라이블러 발산)
  

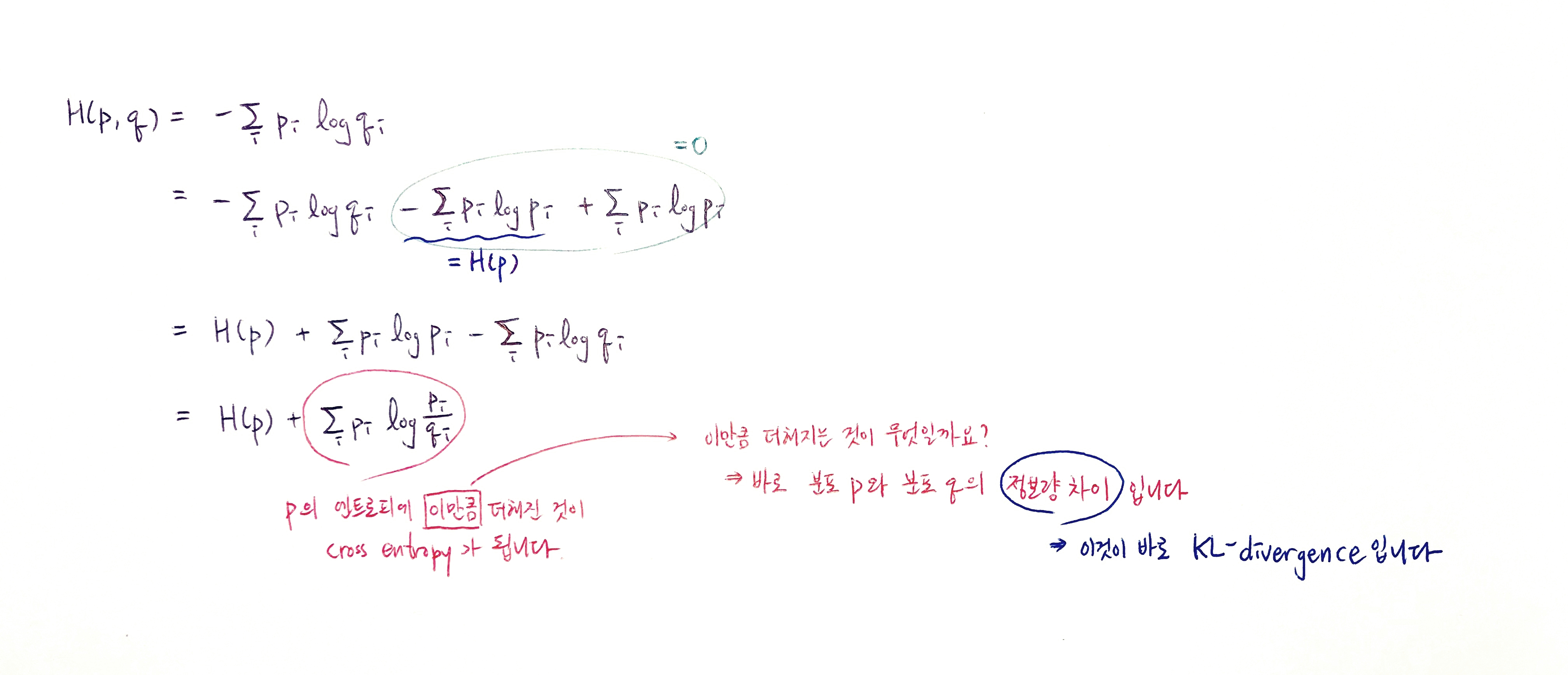
• p의 엔트로피(H(p))에 Cross-Entropy를 더한 것.
  

  출처 : https://hyunw.kim/blog/2017/10/27/KL_divergence.html

Softmax vs SVM

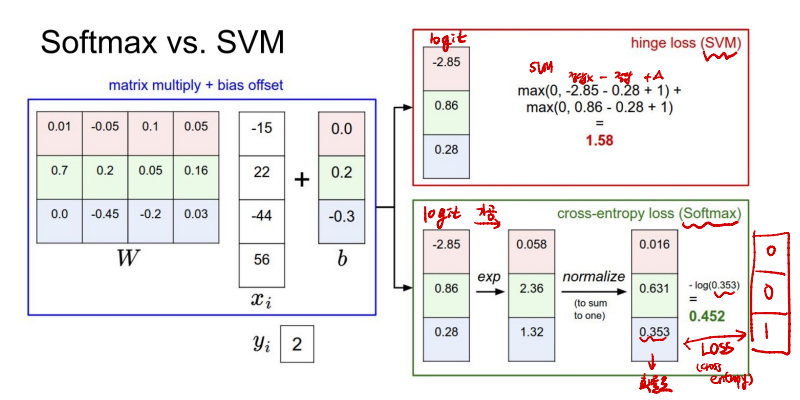
• SVM은 정답이 아닌 값과의 차이를 더한 값을 Loss로 사용한다.
• Softmax는 logits(raw score)를 가공(exp, Sum to 1)한 뒤, 정답 class를 1로한 확률과 Loss를 Cross Entropy를 통해 산출한다.