[AIAS] 4. Gradient Descent

본 내용은 인하대학교 정보통신공학과 홍성은 교수님의 인공지능응용 강의내용을 기반으로 작성한 내용입니다.

앞이 안 보이는 사람이 하산을 해야 한다면?

• 경사가 급한 방향으로 한 발자국 씩 가는 방법이 있을 것이다.
• 이를 기계 학습에 적용한 것이 경사 하강법(Gradient Descent)

Gradient

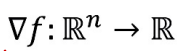
• 편미분들로 구성된 벡터
• f의 그레디언트
• 입력 : n차원 → 출력 : 1차원

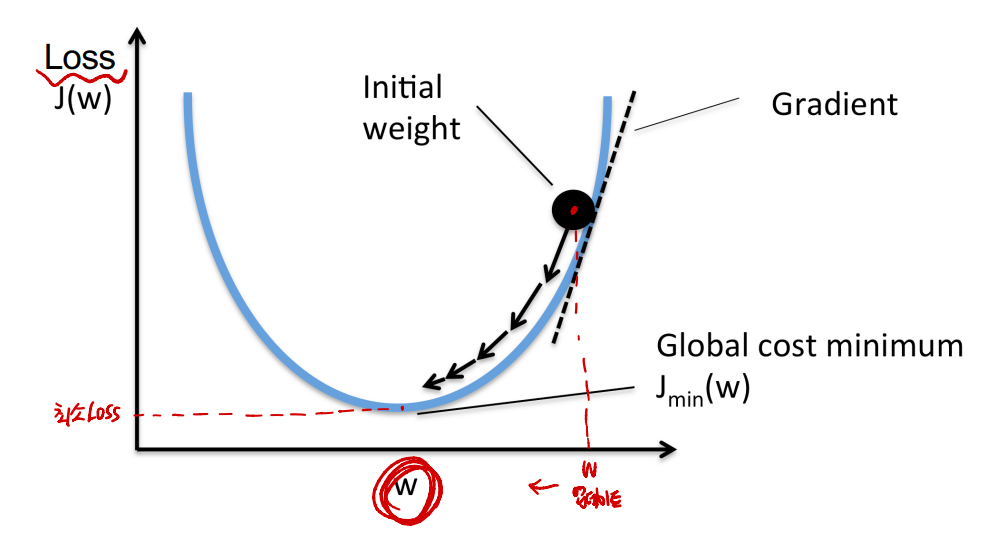
• 오목한 곳으로 들어가게 하여 최소 loss를 찾는다.

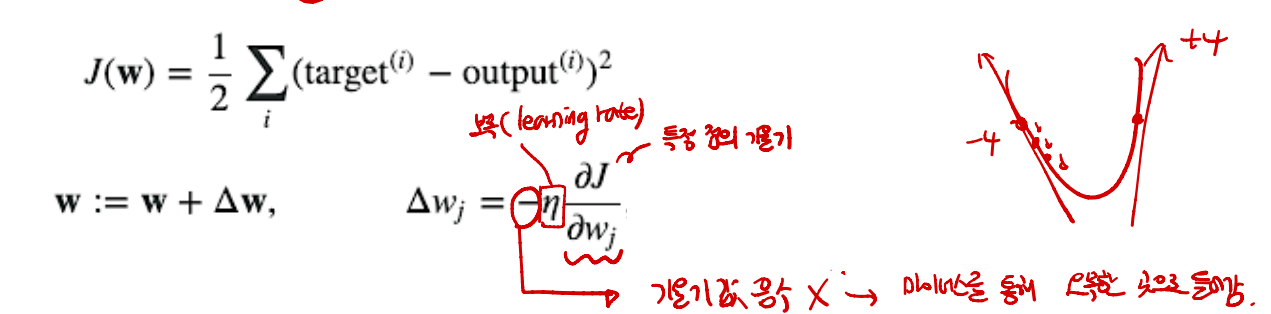
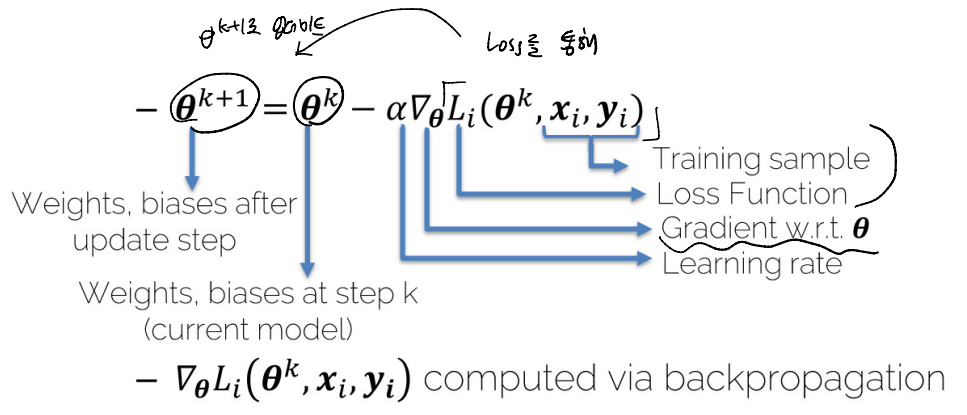
• J(w)가 Loss를 구하는 식, w는 weight
• Loss를 weight에 대해 편미분 한 뒤, Learning rate를 곱해준다. 이후 이를 (-)하여 바깥쪽으로 뻗는 것이 아닌 안쪽으로 들어가도록 한다.
• gredient 식을 구했다면, delta W를 구하고, 이를 통해 W를 지속적으로 update한다.

example

• 2차원일 때,
  
• f(x, y)는 Loss Funtion을 나타냄.
• f(x, y) = 3x^y일 때, , (x, y)는 epoch 한 번 당 각 weight.
• (1,1)에서 gradient(기울기)?
• x에 대한 편미분 = 6xy
• y에 대한 편미분 = 3x^
• gredient f = [6xy, 3x^]
• gredient f(1,1) = [6, 3] (1,1에서의 gradient(기울기))
• delta Wx = -(learning rate=0.01)*6 = -0.06
• delta Wy = -(learning rate=0.01)*3 = -0.03
• Wx = 1 - 0.06 = 0.94
• Wy = 1 - 0.03 = 0.97
• 2차원 Weights = [0.94, 0.97]

Learning Rate

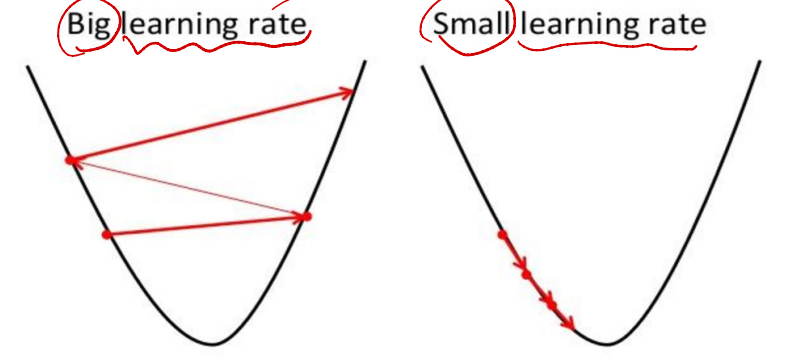
• gradient에 곱해지는 hyperparameter로 학습 시 Weight의 변화량을 조절한다.
• Learning Rate가 클 때, 최소 Loss를 찾지 못하고 왔다갔다 하거나 튕기는 현상 발생(overshooting)
• Learning Rate가 작을 때, 최소 Loss에 도달하지 못하는 문제 발생

Gradient Descent

• 경사하강법
  
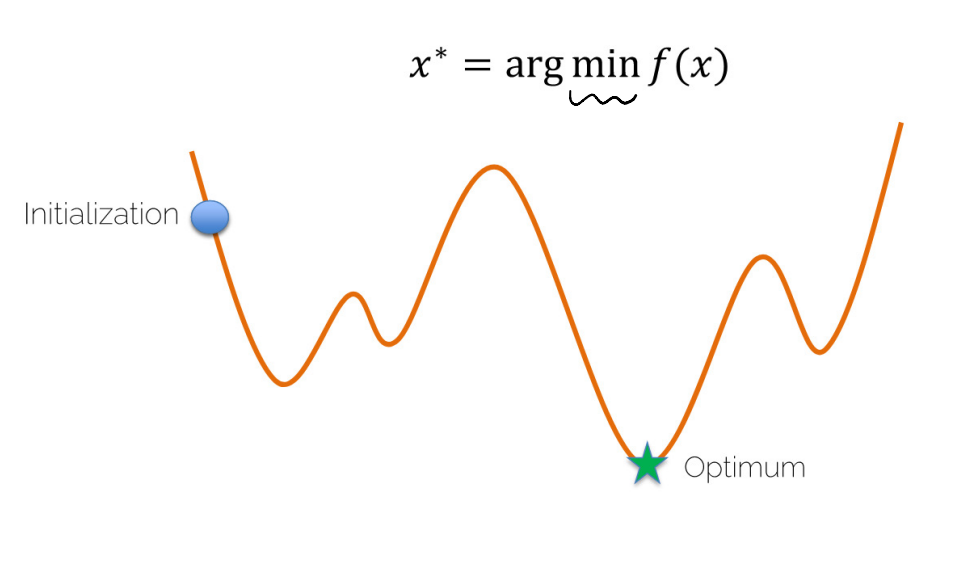
• 임의의 점을 "초기 Weight"로 지정하고, 주변 값들보다 자신이 작을 때, 이를 최저 Loss로 인식한다. 이는 미분을 통해 구할 수 있다.
  
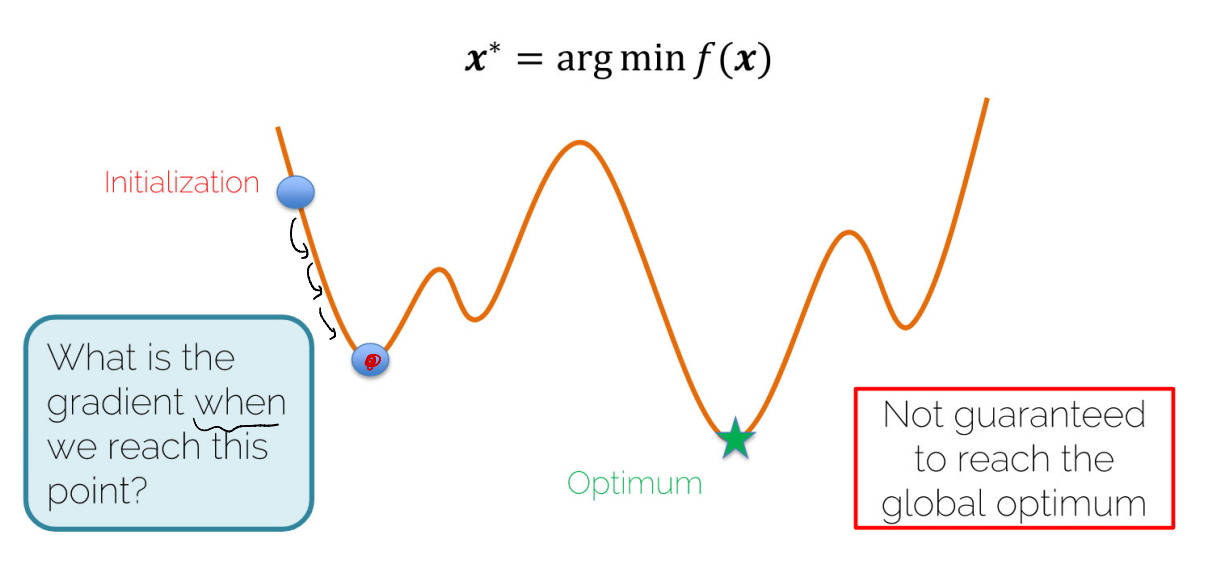
• 위 그림과 같은 상황일 때, 이상적인 최저 Loss와는 다른 값이 최저 Loss로 선정된다. 하지만, 이를 해결할 수 있는 방법은 없다.
  
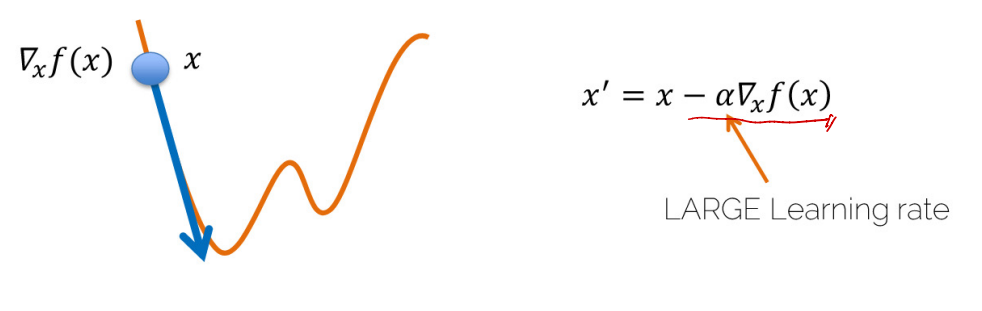
• 기울기가 감소되는 방향을 위해 Learning Rate 앞에 (-)를 붙여주고, Learning Rate의 커짐에 따라 한 Step의 크기가 커진다.

Single Traning Sample

• 아래는 Gradient Descent를 통해 Parameter를 업데이트하는 수식이다.
  

Multiple Training Sample

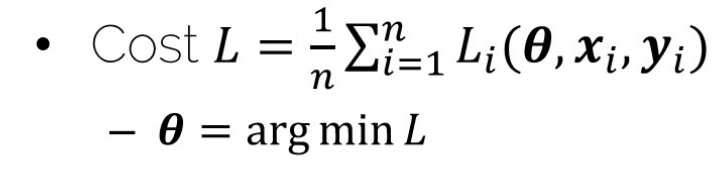
• Cost L은 각 Set에 대한 Cost의 평균을 측정하고, 그 Set Cost 평균의 최소값을 찾는다.
  
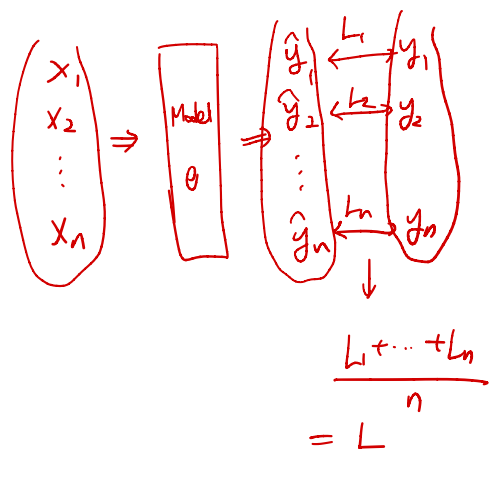
• Loss를 구하는 전체적인 flow는 위와 같다.
  
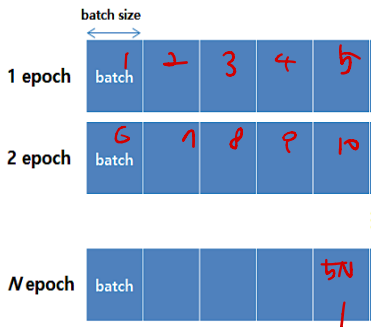
• sample의 개수 n이 너무 클 때, Memory Error가 발생하므로, GPU 성능을 고려하여 일정 개수로 Grouping하는데, 이 그룹을 Batch라고 한다.

여기서 중요한 단어 3가지!

• Epoch : 전체 데이터셋을 학습하는 횟수
• Batch : 메모리가 수용 가능한 데이터 개수만큼 자르는 단위
• Iteration : (=step) batch size만큼 학습하는 것을 1 Iteration이라고 한다.
  
• 위 그림을 통해 알 수 있는 정보는 아래와 같다.
• 전체 데이터를 메모리가 수용 가능한 batch size만큼 잘라, 5개의 batch가 만들어졌다.
• 5개의 batch를 학습. 전체 데이터를 학습하는 것이 1 epoch이다.
• 1개의 batch를 학습하는 것이 1 iteration이다.
• 1epoch는 5 iteration과 같다.

SGD(Stochastic Gradient Descent)

• Batch 단위로 Loss를 계산하는 Gradient Descent 기법으로, 데이터 전체를 한 번에 보고 Loss를 계산하는 batch gradient descent와 대비되는 개념이다.
  
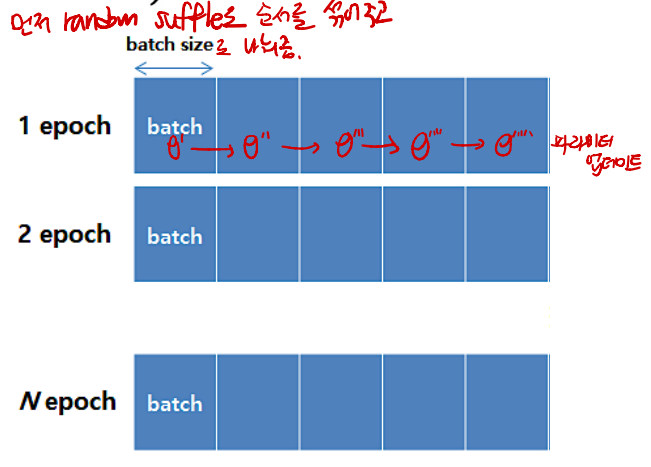
• 그림과 같이 전체 데이터를 random하게 섞어주고 batch size로 나눈다.(5개의 batch로 나누었음)
• 이로 인해 Local Minima에 쉽게 빠지지 않을 수 있다는 장점이 있다.
  
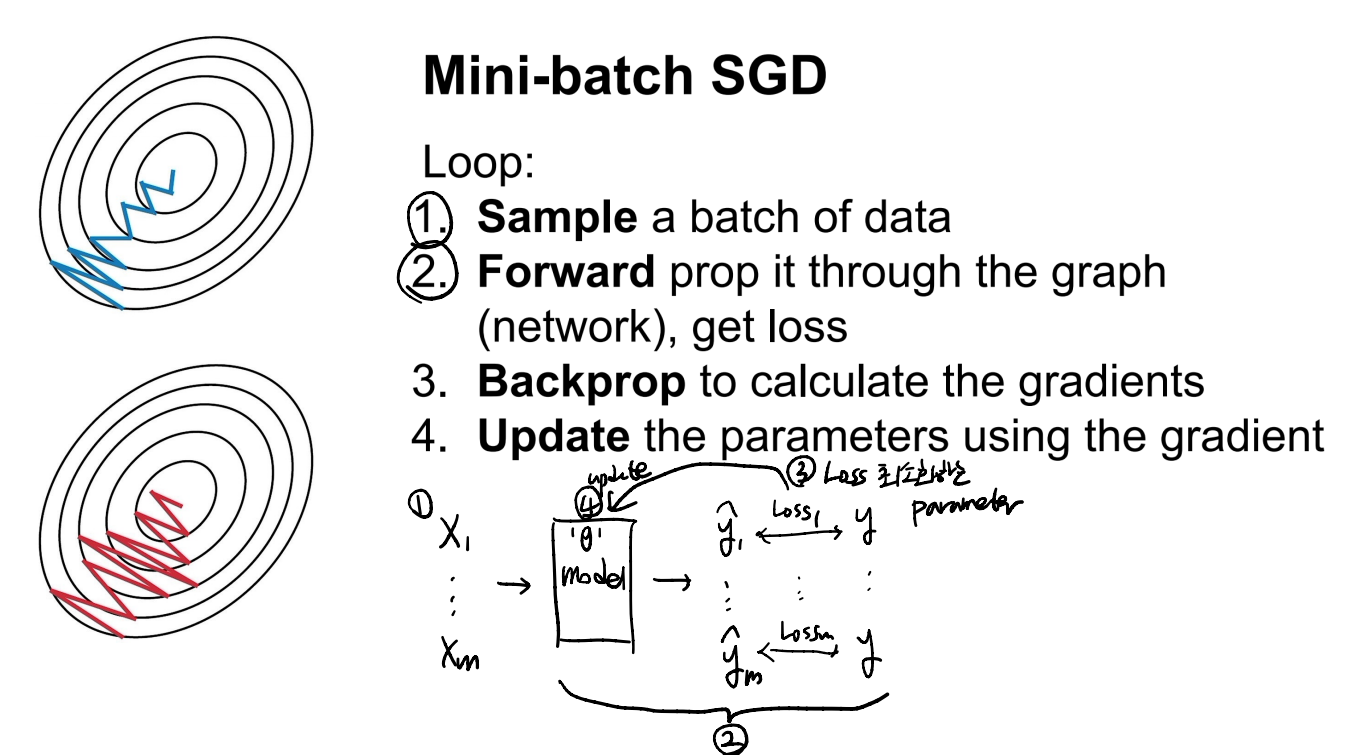
• ① 데이터를 batch size로 나눈다.
• ② 모델을 통해 target y를 예측한다.
• ③ Loss를 계산한다.
• ④ Loss를 최소화하는 parameter를 update 한다.
  
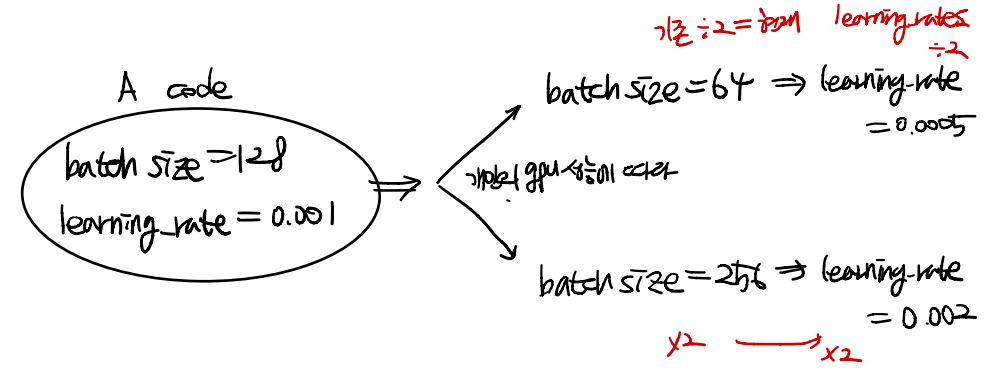
• batch size는 개인 GPU 성능에 따라 결정하며 2의 지수승으로 한다.
• batch size가 2배 커진다면, Learning Rate도 같이 2배 하는 것이 효율적이다.

Learning Rate Scheduling

• Q : 가장 적절한 Learning Rate는 몇일까?
  
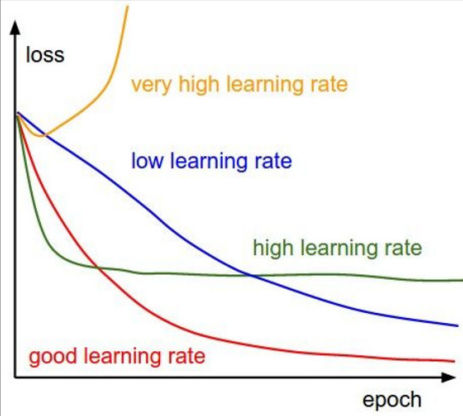
• 너무 클 때, Loss가 오히려 증가
• 적당히 클 때, Loss가 빠르게 증가하다가 최저점에 도달하지 못한다.
• 낮을 때, Loss가 너무 천천히 감소, local minima에 빠지게 되면 더이상 감소하지 않는다.
  
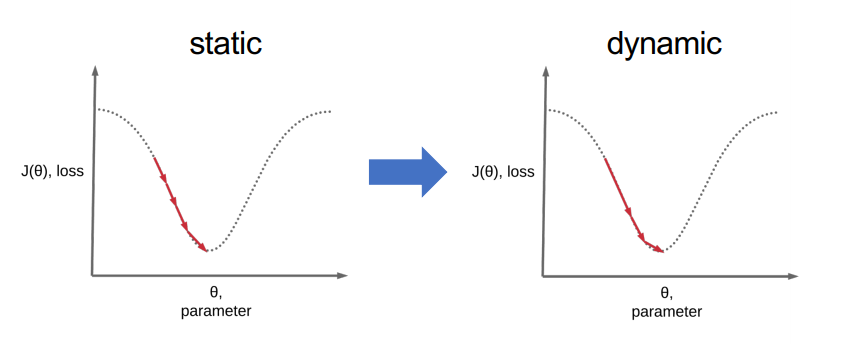
• A : 그런 것은 없다! 하지만, 초기의 Learning Rate를 크게 → 이후에 작게 하는 것이 좋다. (Dynamic하게)
  
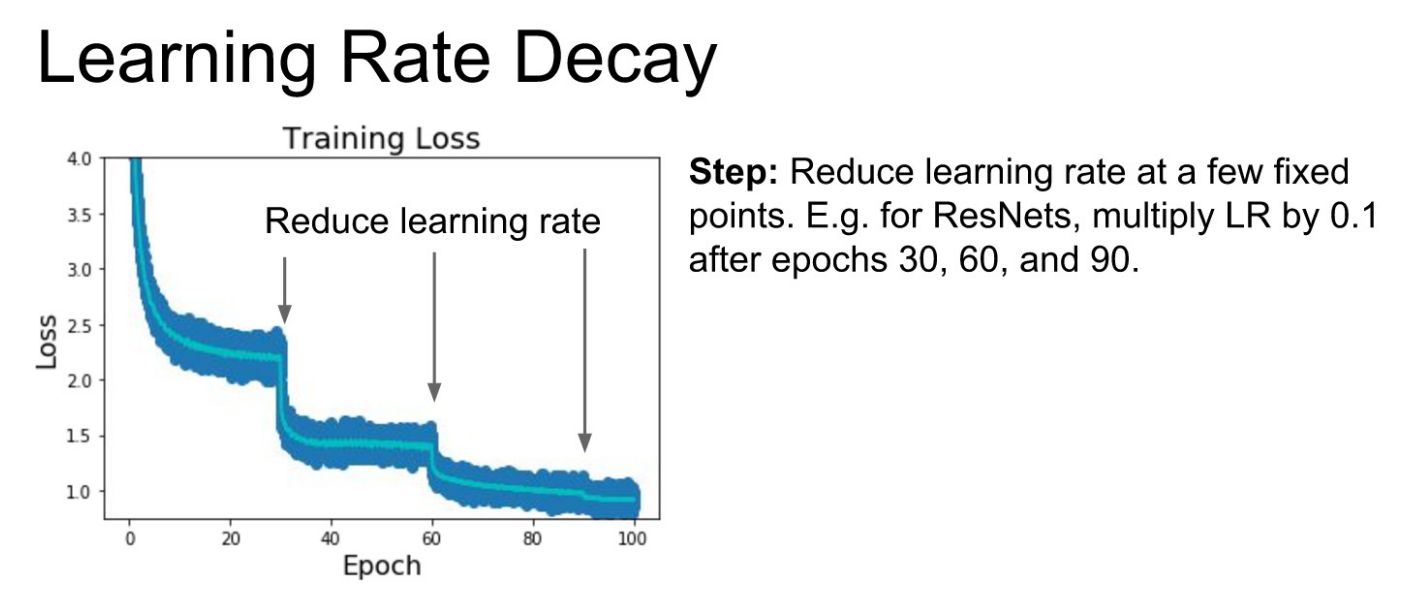
• 처음에는 Learning Rate를 크게 하고, 이후 30epochs, 60, 90 ,,, 마다 Learning Rate를 10으로 나누어 낮추는 방식.
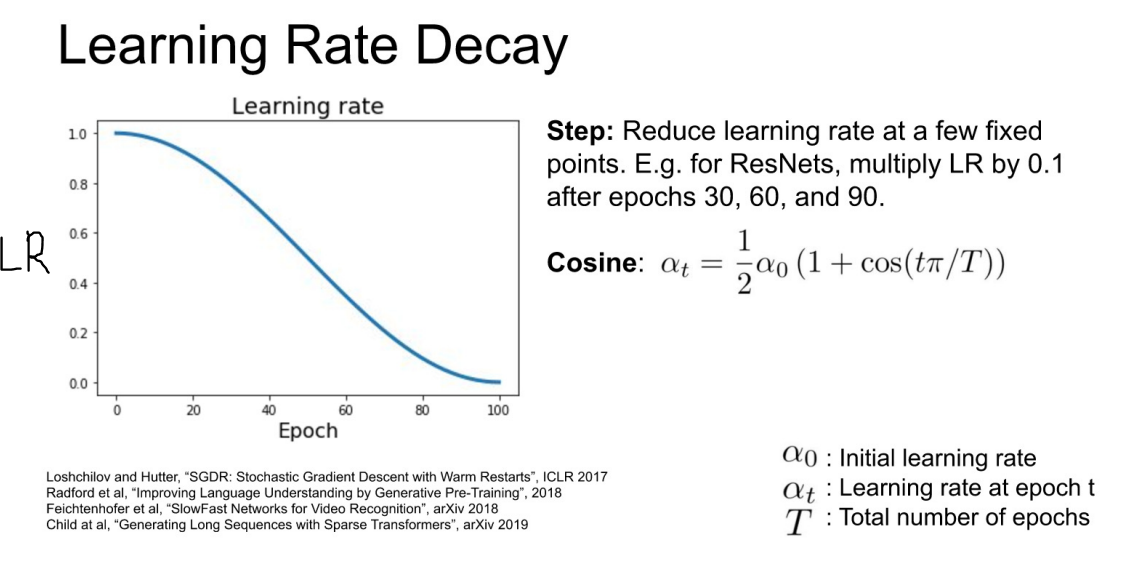
• 너무 Discrete 하다! 해서 나온게 아래 Cosine 그래프 방식
  
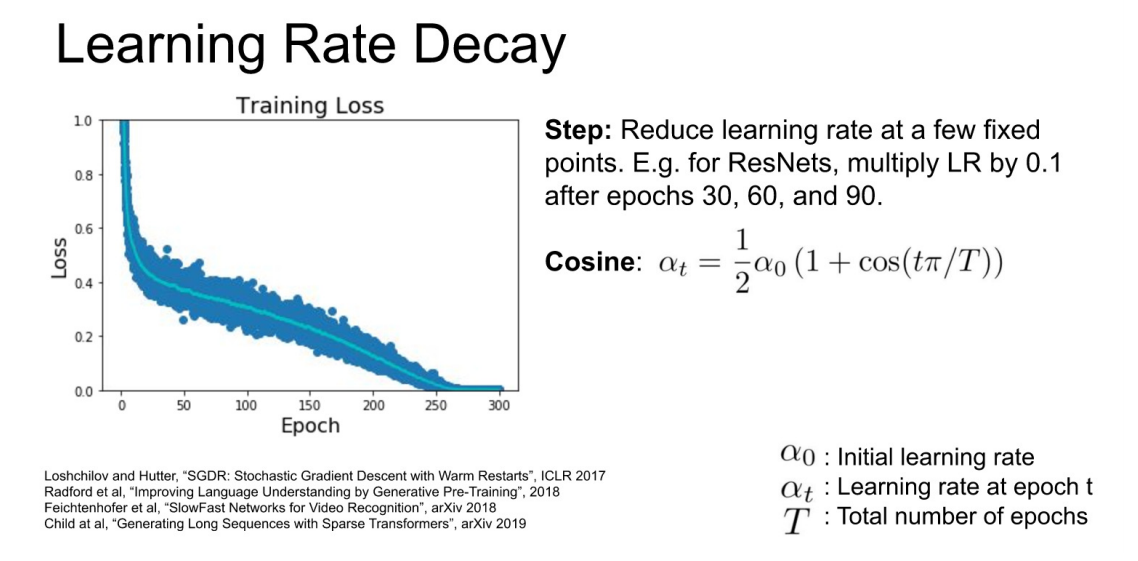
• 위의 Learning Rate로 학습을 시키면, 아래와 같은 Loss 그래프를 확인할 수 있다.
  
• 추가로 그냥 Linear하게 Learning Rate를 감소시키는 방법도 있다.(Inverse sqrt 등 방법이 있지만 잘 사용하진 않는다.)
• 특이한 개념 : Linear Warmup
  
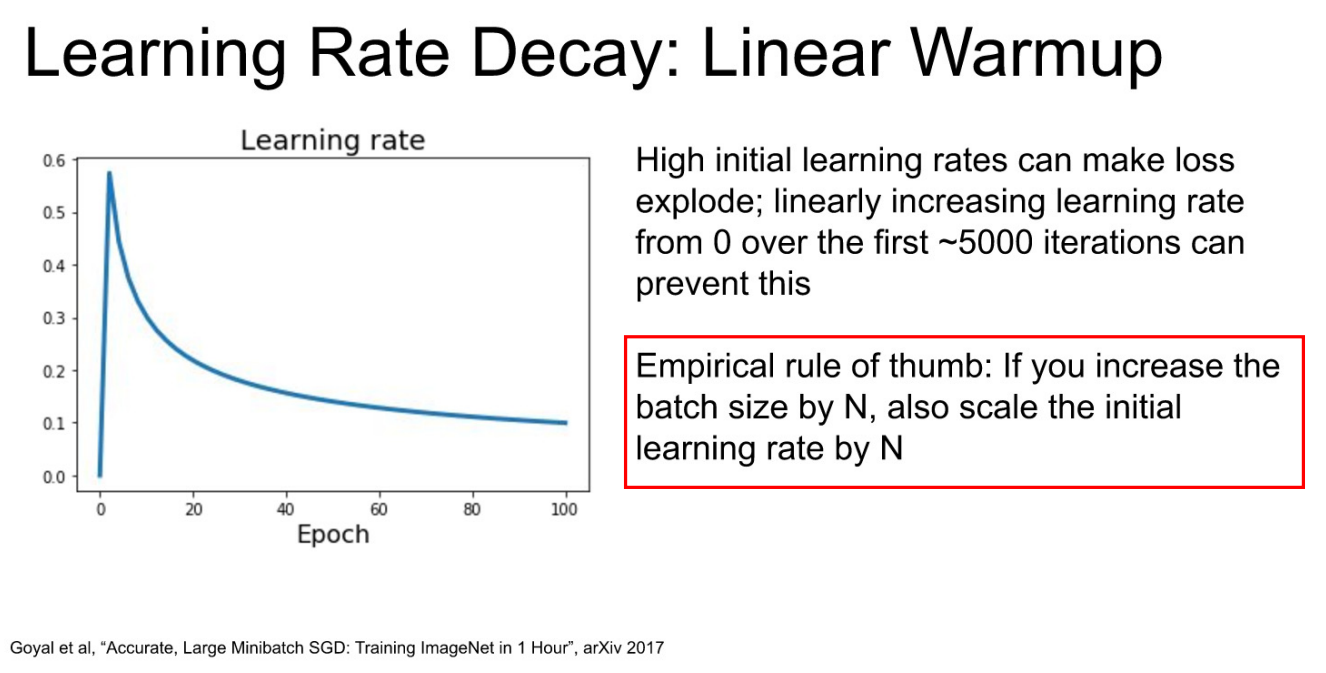
• 초반에 Learning Rate를 낮게 가져가서, 원하는 Learning Rate에 도달했을 때부터, Cosine처럼 서서히 감소 시킨다.
• Why? "Emprical rule of thumb"
  
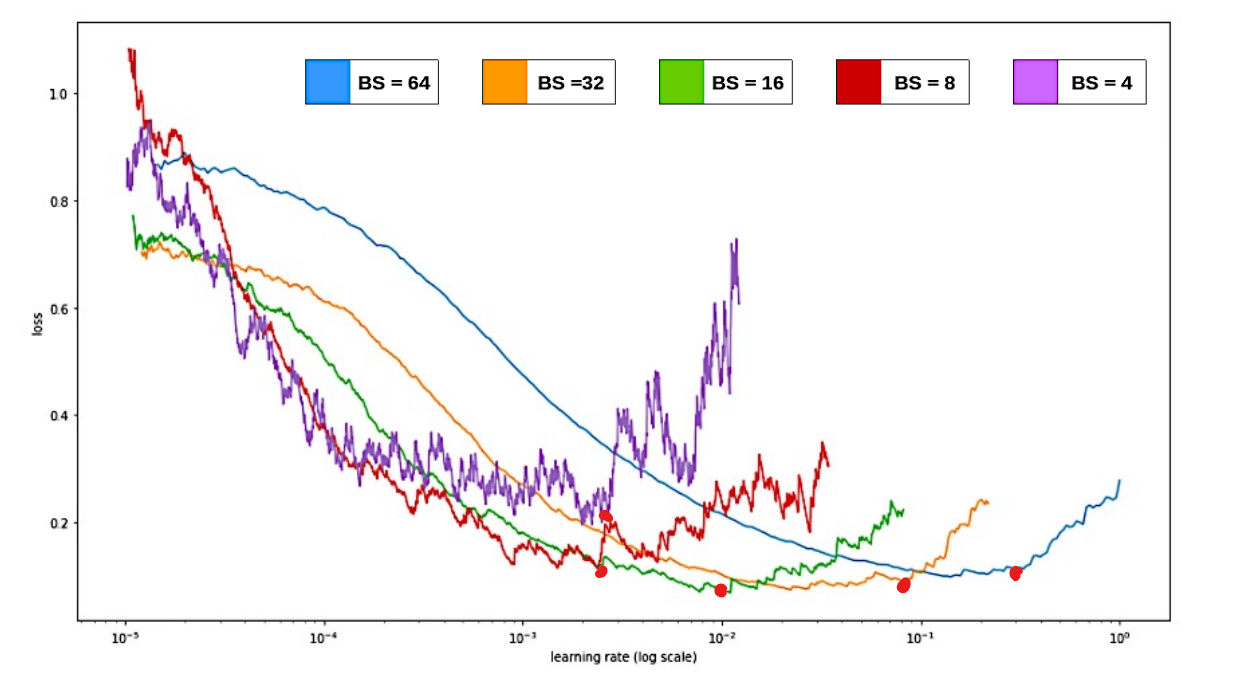
  • Emprical rule of thumb : Batch size가 N배 증가한다면, Learning Rate도 N배 증가 시켜야 같은 성능이 나온다.
• batch size 20, Learning Rate = 0.01 기반으로 학습된 코드. 내 GPU 성능이 좋아서 batch size 40으로 학습을 시킬 때, Learning Rate도 0.02로 설정하고 학습해야 한다.
• 하지만 batch size가 40인 것을 감안 하더라도 처음부터 Learning Rate를 0.02로 설정하면 발산 가능성이 존재한다.(Loss Curve의 시작점이 어디일지 모르기 때문에)
• 그렇기 때문에 처음에는 작은 Learning Rate부터 예정되어있던 Learning Rate까지 차근히 올린 뒤, 이를 낮추는 방식으로 하면 안정적으로 모델을 학습할 수 있다.