[AIAS] 5. Introduction to Neural Network(NN)

본 내용은 인하대학교 정보통신공학과 홍성은 교수님의 인공지능응용 강의내용을 기반으로 작성한 내용입니다.

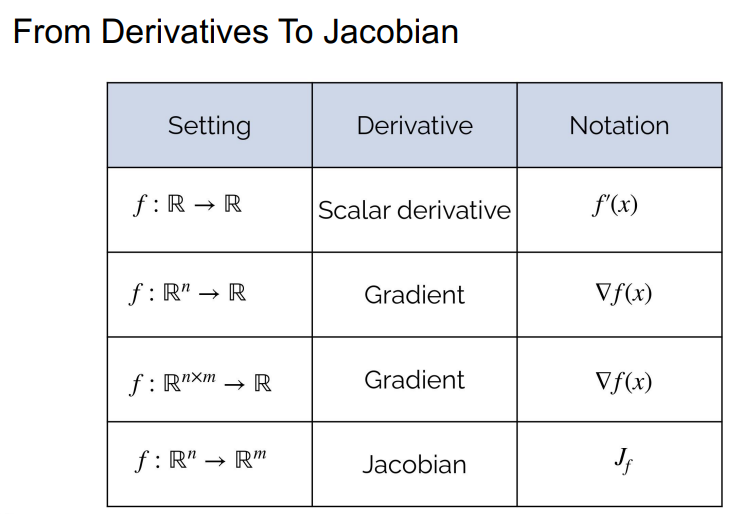
Tensor

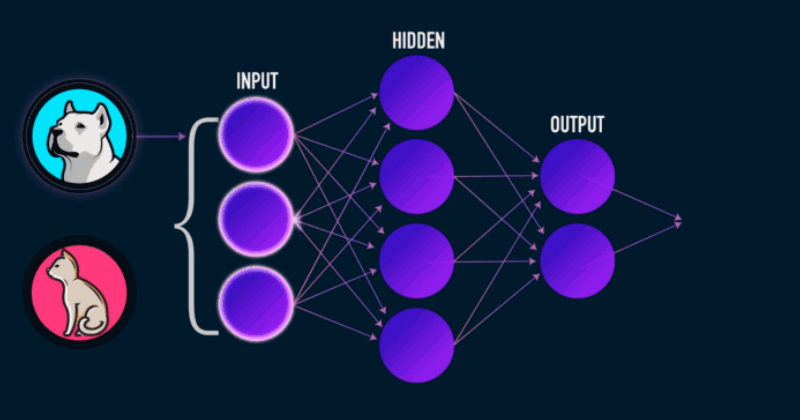
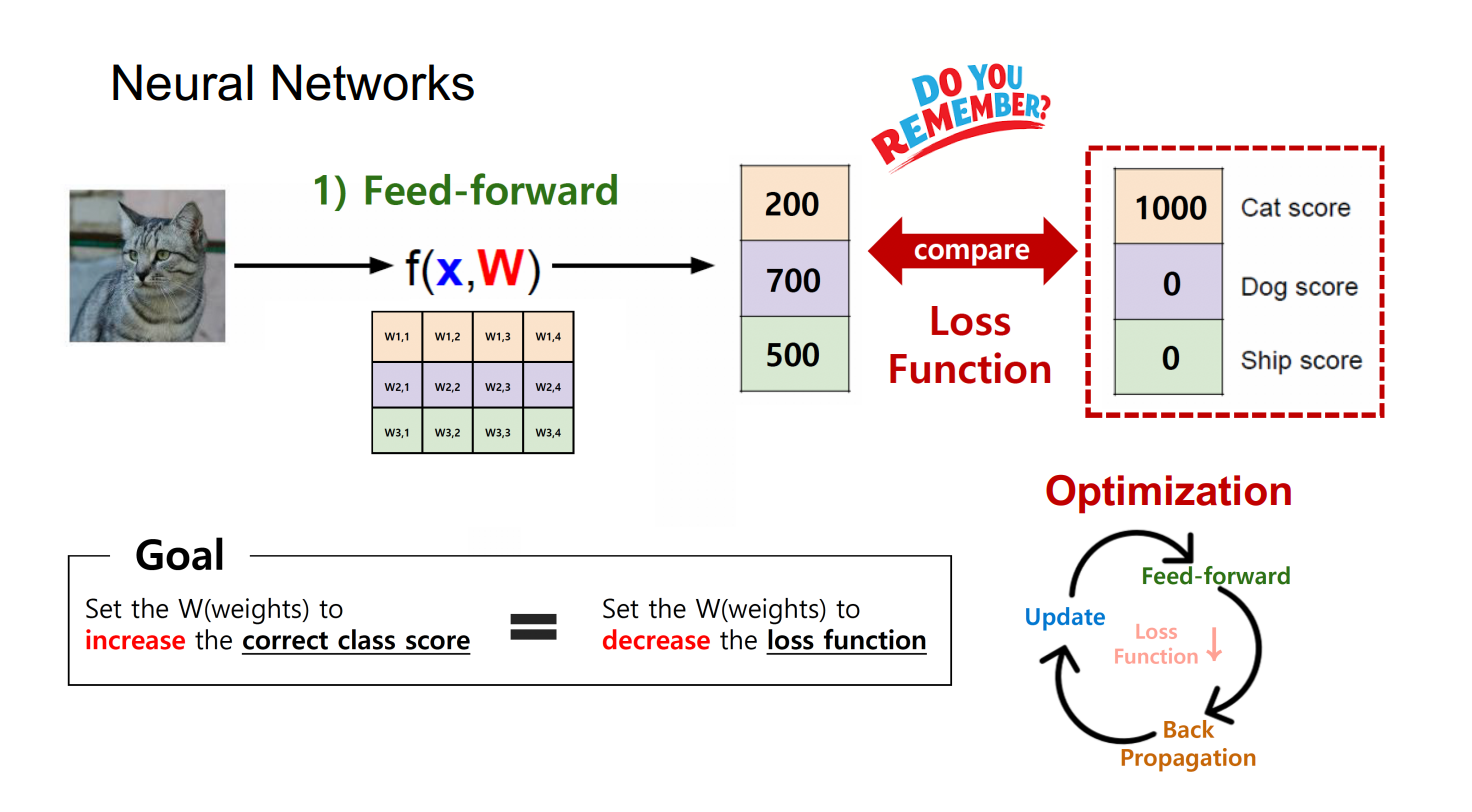
Neural Networks(NN)

• Artificial Neural Networks(ANN)이라고도 한다.
  
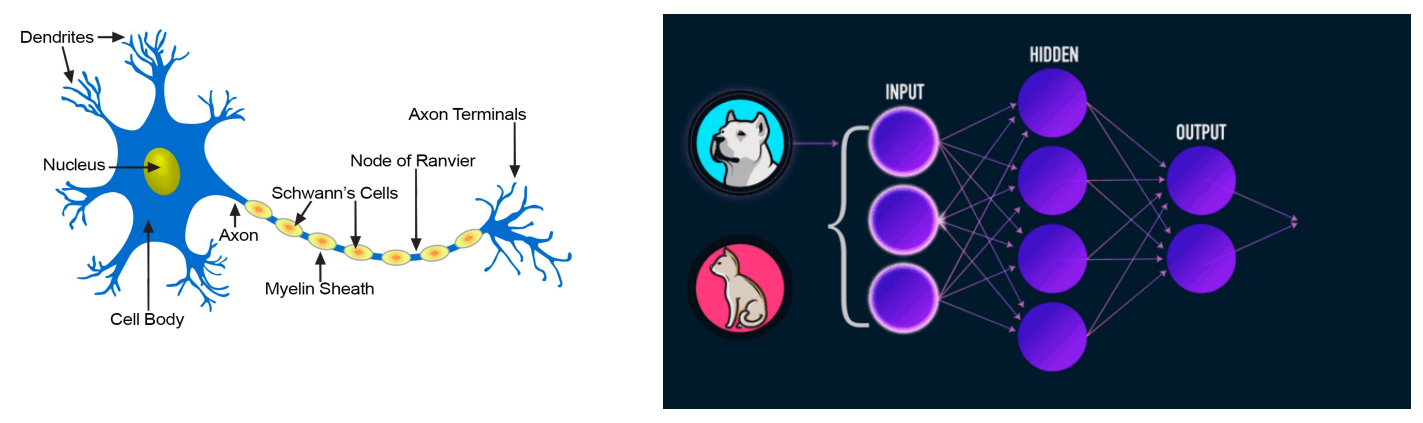
• input이 hidden layers를 거쳐서 output으로 나오는 구조

Linear (most simple)

• hidden layer의 개수가 1개(single layer)인 모델이다.
• 간단하게 f(x,W) = Wx로 표현하기도 한다.
  

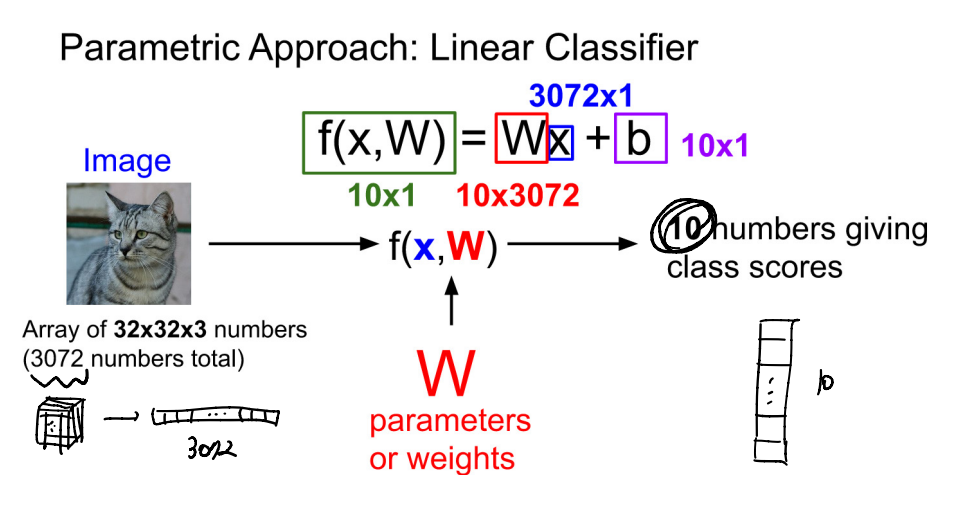
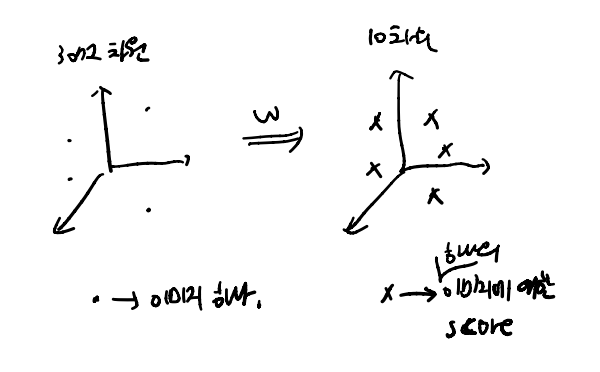
• 이미지가 score로 변하는 과정을 시각적으로 표현하면 위 그림과 같다.

2-layer or 3-layer NN

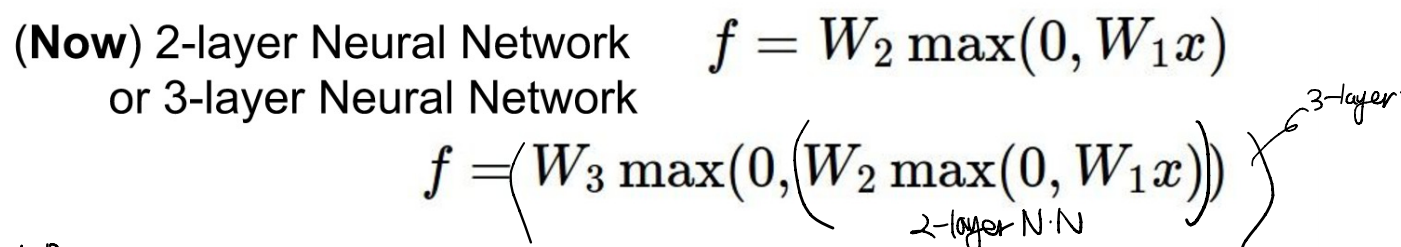
• 단순한 single layer의 결과값이 또 다른 layer의 input으로 들어가는 구조이다.
  
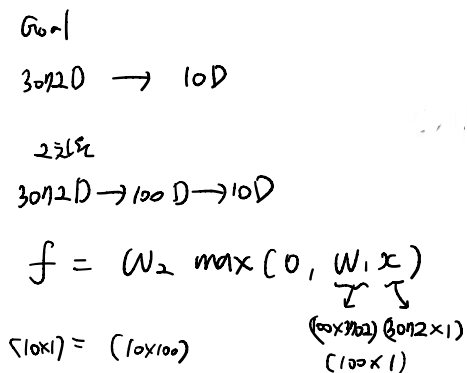
• 최종 목표가 10차원으로 줄이는 것일 때, hidden layer 개수에 따라 목표를 향해 순차적으로 줄여나갈 수 있다.

Code

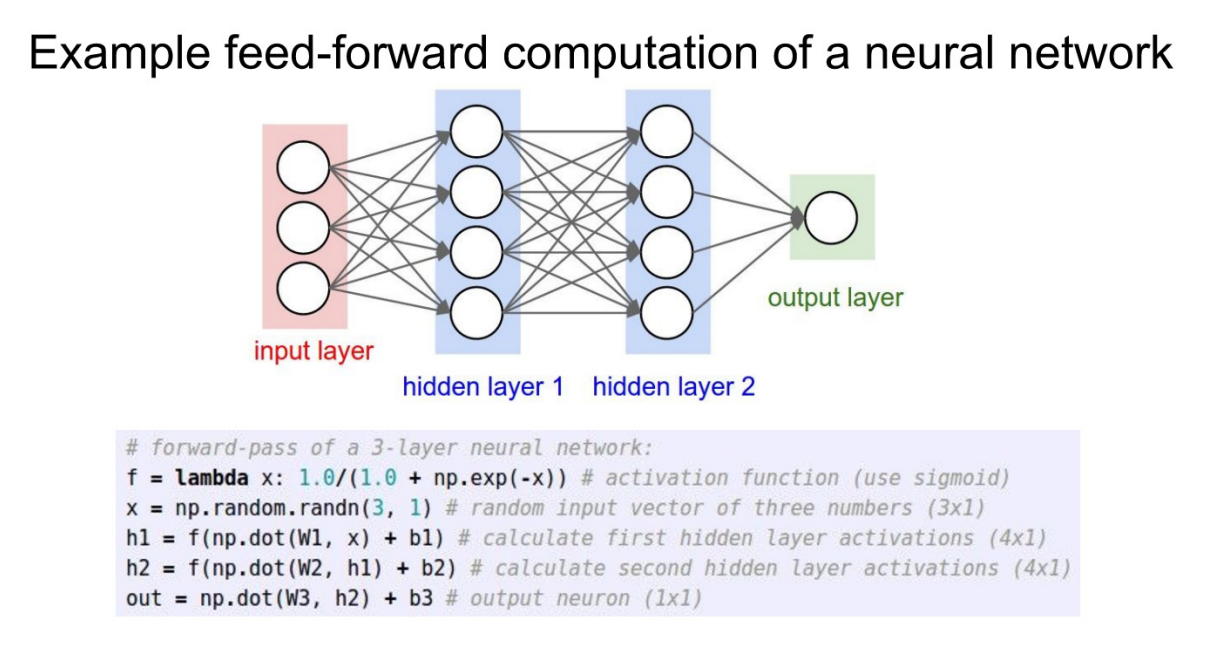
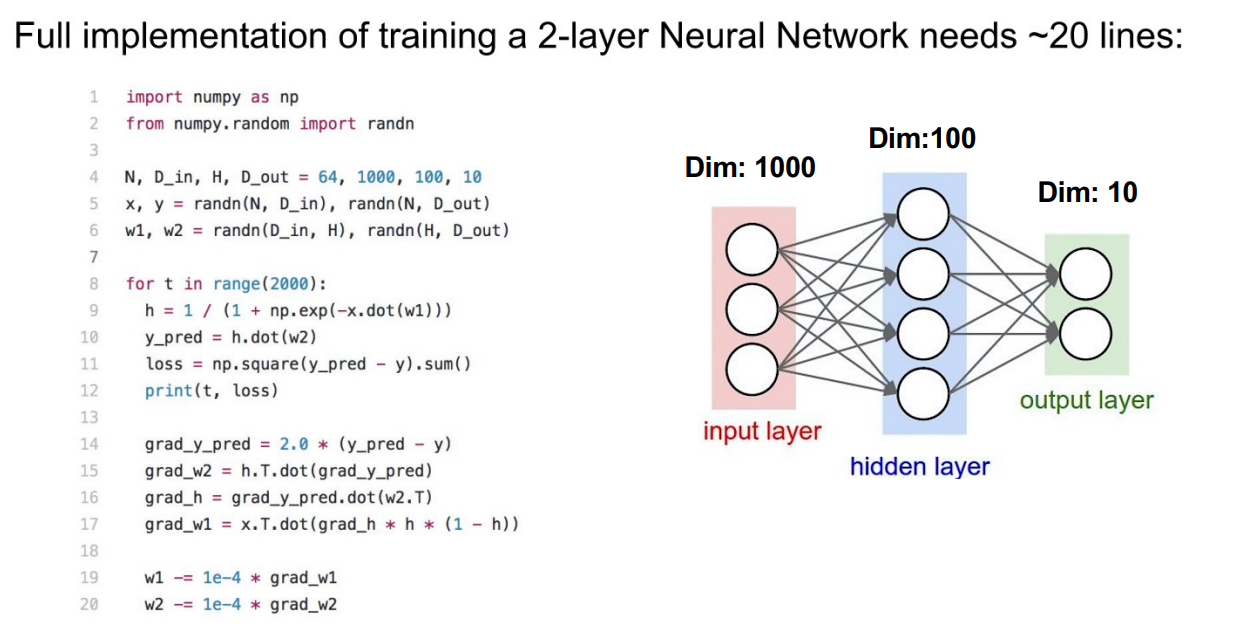
• w가 두개인 것으로, 2-layer NN(1-hidden layer)임을 알 수 있다.

Activate Function

• 활성화 함수 : 이전 Layer의 output을 다음 Layer의 input으로 넣는 과정에서 생길 수 있는 문제를 방지하는 역할을 한다.
  
• max(0, z)는 활성화 함수로, 이전 Layer의 output이 양수일 때, 그대로 다음 Layer의 input으로 넣고, 음수라면 0으로 바꿔주는 역할을 한다.
  
• 만약 활성화 함수가 없다면, 층을 아무리 깊게 쌓아도 결국 하나의 층으로 표현이 가능하게 되므로, 결국 Linear하게 된다.

다양한 활성화 함수

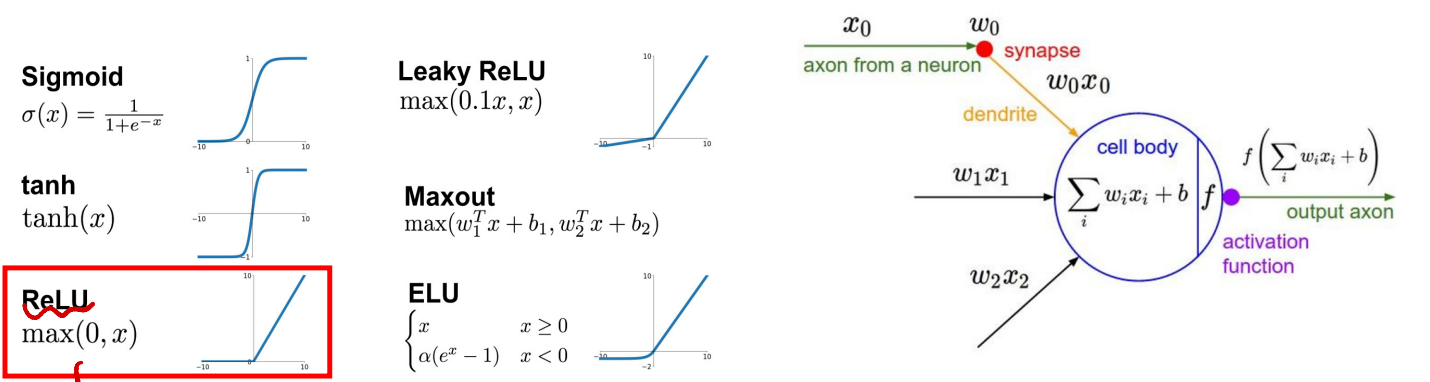
• Sigmoid : 값을 0~1사이로, 평균 주변 값이 다양한 y를 갖는다.
• ReLU : 음수 값은 다 0으로, 양수는 그대로 한다.(max(0, x))
• 주로 ReLU를 사용

Regularization

• 우리는 위 과정을 통해 Loss를 찾고 Loss를 최소화 하는 Weight를 찾는다.

• 만약 Loss=0이라면?
  

• Loss가 0이면, W를 2배 크게 해도 Loss가 변하지 않는다.
• 결국 서로 다른 Weight 값임에도 Loss가 0으로 같다면, 어떤 Weight가 더 좋은 Weight인지 알 수 없다.
• 그에 대한 기준이 될 수 있는 것이 Regularization 이다.

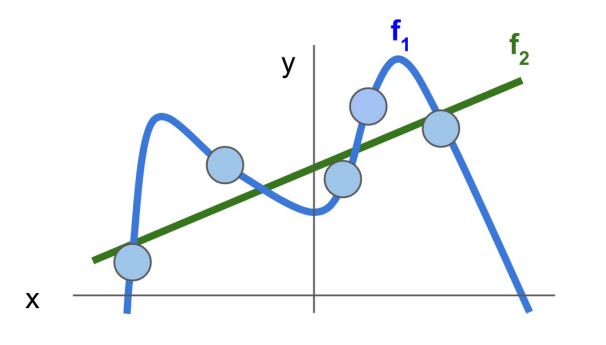
• train data에 대해 model을 fitting 한다고 할 때, f1이 train data에서 좋은 성능을 낼 수 있다.

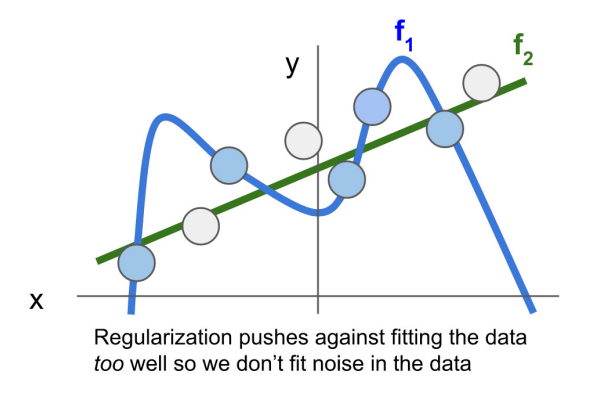
• 하지만 test data가 흰색과 같이 주어졌을 때, 더 잘 맞추는 것은 f2일 것이다. 이렇듯 train data에 fitting을 할 때, 모델이 좀 더 단순하게 학습하게 하는 것을 Regularization이라고 한다.

• 우리가 앞서 배웠던 Loss Function은 Data Loss(predicted y와 test y의 차이의 평균)이고, 여기에 Regularization Loss를 더한다.
• 두 Loss를 합할 때, 두 Loss의 영향도가 다를 수 있으므로 Regularization Strength를 hyperparameter로 한다.
• Data Loss를 낮추는 것이 더욱 중요하기 때문에 Regularization Strength는 0.001,,, 로 한다.

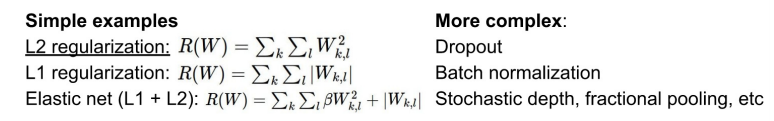
• Regularization Loss를 구하는 방식
• L2 Regularization은 Weight를 제곱하는데, 제곱은 작은 값을 더 작게 만들어 주므로, Weight가 작으면 Regularization Loss가 더 작아진다.

• 실제로 일반화 성능을 평가해보자.
• w1은 값이 한 쪽으로 쏠려 fitting 되어 있고, w2는 균등히 퍼져있다.
• 제시된 x와 w1, w2를 L2 Regularization을 통해 계산하면, x와 w2를 통해 계산한 값이 더 작으며, 이는 Regularization이 잘 되었음을 알 수 있다.

총 정리

• 우리에겐 x, y 데이터 쌍이 주어진다.
• 데이터(x)와 Weight(W)를 통해 데이터의 score를 산출할 수 있다.
• Loss function은 어떤 모델을 쓰느냐에 따라 달라지는데, 결국 전체 Loss에 대해 산출하기 위해서는 Data Loss와 Regularization Loss를 구한 뒤 합한다.
• 이 때, Regularization Loss는 hyperparamter를 통해 Regularization의 Strength를 조절한다.
• Data Loss : W, x를 통해 예측된 y^과 y 간의 차이
• Regularization Loss : 모든 W에 대한 계산(L1, L2 Regualrization)
  
• 결론 : Regularization의 목적 = 모델을 간단하게 만들자! = W가 작을수록 모델이 간단하다!

Backpropagation

• 역전파
  
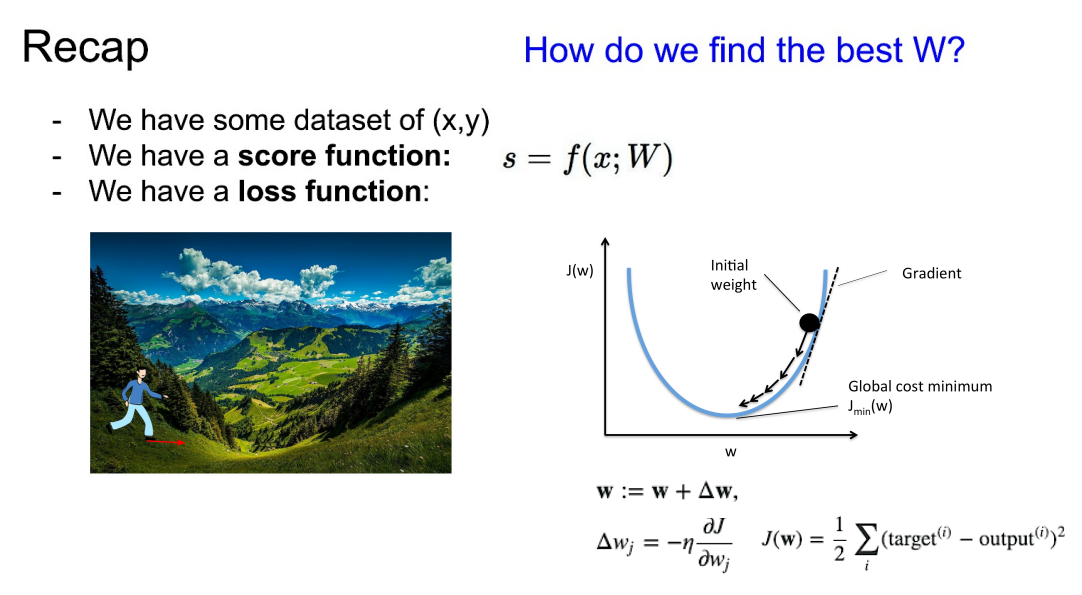
• 복습을 해보면, 최소 Loss를 가지는 w를 찾기 위해 경사 하강법을 사용한다.
• 이는 Loss Funtion을 Weight에 대한 함수로 볼 수 있다.
• 모델이 너무 깊거나 or Loss Funtion이 너무 복잡하면 -> 차원별로 편미분 -> 한 번의 Weight에 대한 Loss를 구하는 것이 -> Trick으로 쓰는 것이 Backpropagation

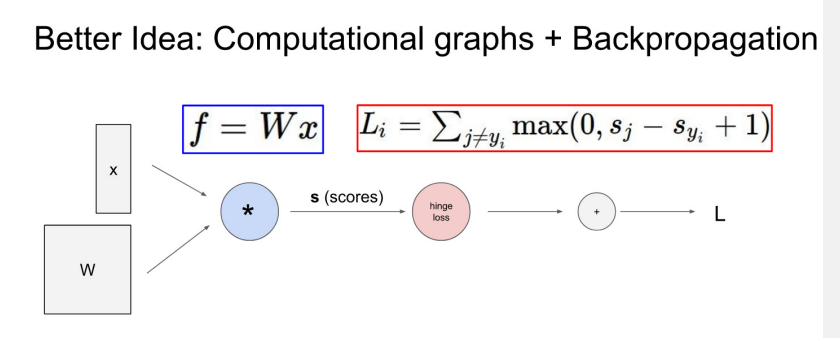
• i는 index, j는 class의 종류 -> Li = SVMClassifier를 사용할 때의 Loss Function, Neural Network는 Linear하다.
• 여기에서 W가 L에 주는 영향도를 파악하기 위해 backpropagation이 필요하다.

Simple Example

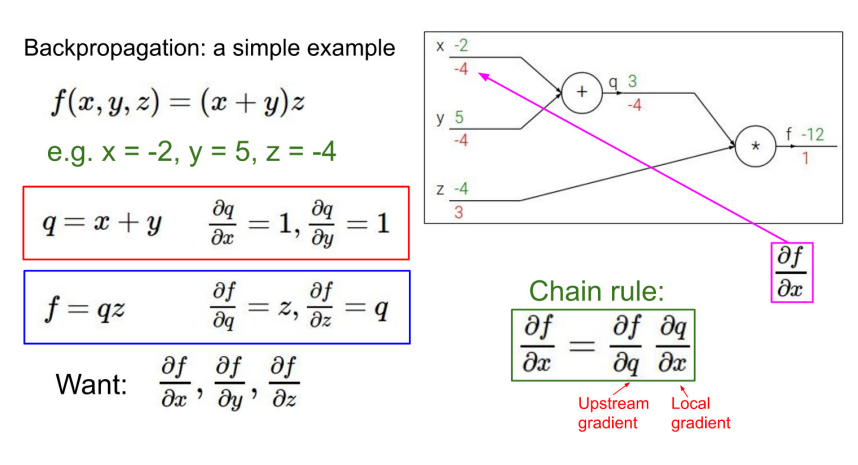
• 간단한 식을 통해 이해해보자.
• f를 x에 대해 편미분 한 값 = f라는 Function에 x가 얼만큼 영향을 주는가.
• 역전파를 하는 이유 : 각 단계에서 편미분 값을 구하면, 한 번에 계산하기엔 복잡하더라도, 출력에서 입력 방향으로의 미분인 Upstream gradient과 Chain Rule에 의해 계산이 가능하다.
• 이를 통해 아무리 복잡한 문제도 쪼개고 쪼개다 보면 문제를 해결할 수 있다는 Backpropagation의 철학을 알 수 있다.

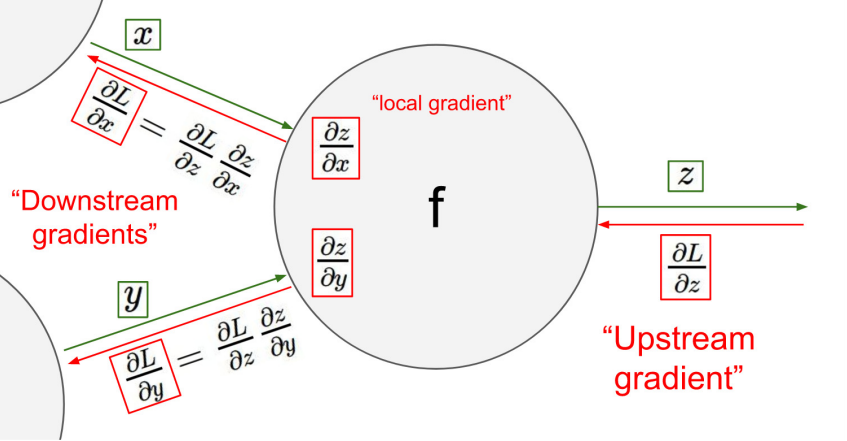
• Downstream gradients = Upstream gradient x Local gradient 를 통해 구할 수 있다.
• Downstream gradients는 이전 단계의 관점에서 보면 Upstream gradient가 되기 때문에 쭉쭉 앞으로 가면서 Downstream gradients를 계산할 수 있다.

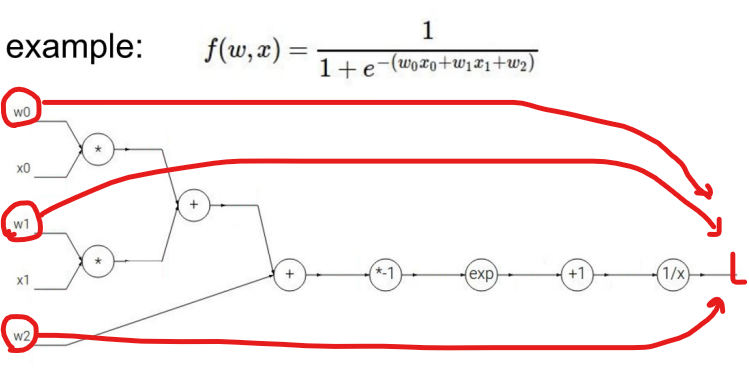
• 더 복잡한 식으로 이해해보자.
• w0,w1 -> 입력 차원 2개(w2는 bias), Linear한 case
• sigmoid 식 : 1/(1+exp(-x))
• 전체 식을 아래 그래프로 표현한 것이다.
• 영향력은 gradient고, gradient descent 방식으로 w' = w + delta w
• Loss에 대해서 backpropagation을 통해 w0, w1, w2가 Loss에 미치는 영향력을 구하고, gradient 구하는 식에 대입하여, Weight를 update 한다.

• ★ gradient 직접 계산해보기

• 내가 계산하고 있는 값이 local gradient인지 upstream gradient인지 잘 구분하여 downstream gradient 구하기
  
  
  
  
  
  
  

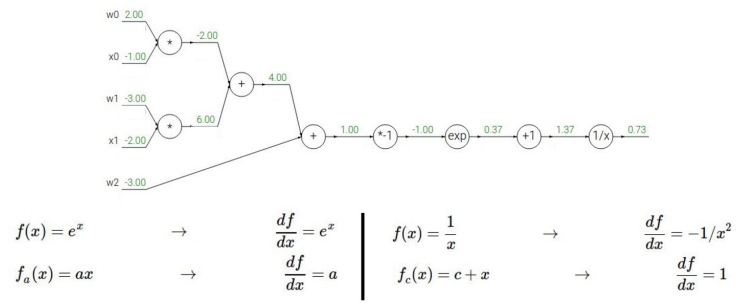
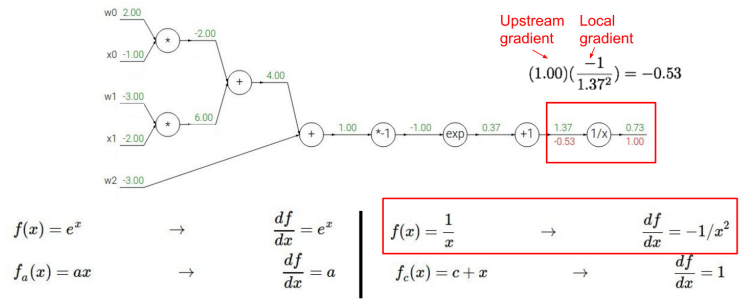
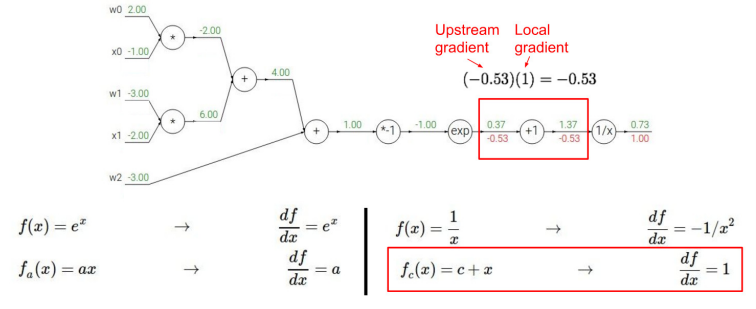
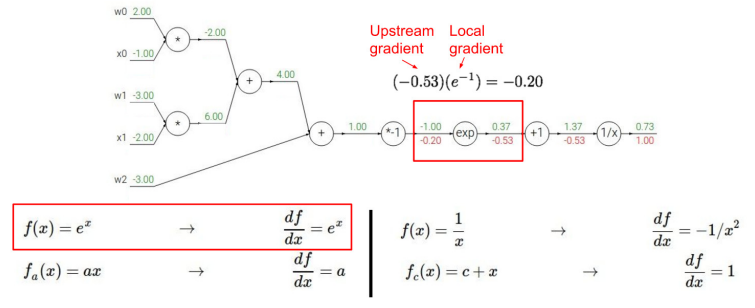
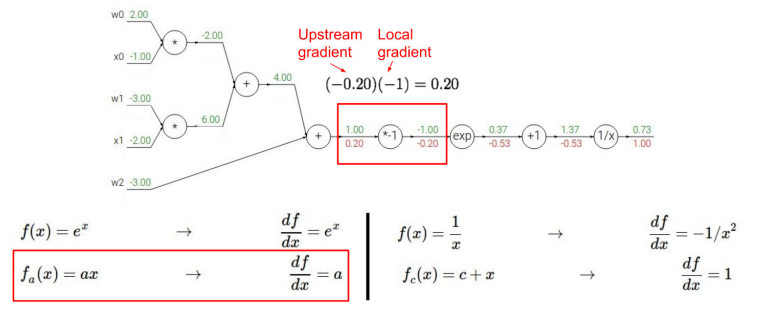
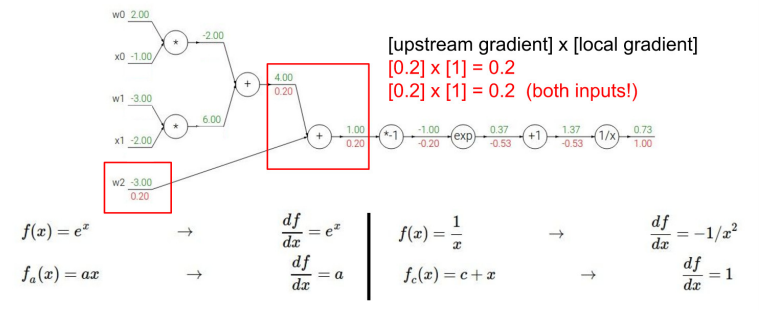
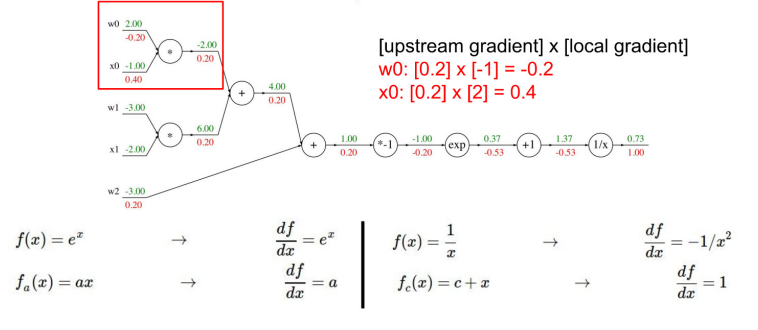
• 이를 크게 보면 1/(1+exp(-x))(sigmoid 식)과 같은데, 각각의 단계에서 미분하지 말고, 전체 식을 미분하면 아래와 같다.
  

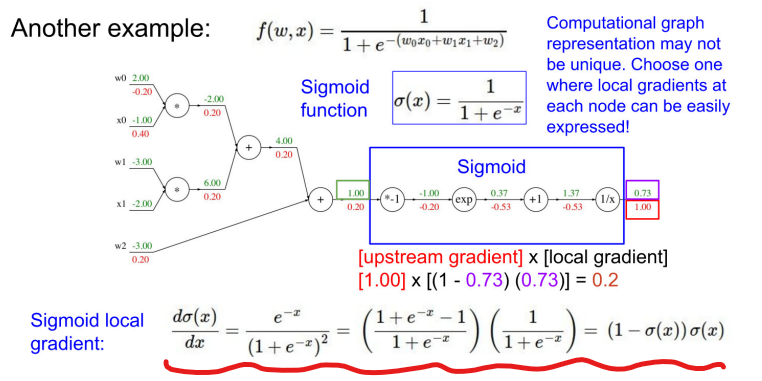
• 모듈화 하여 간결해졌음에도 결과는 0.2로 같음을 알 수 있다.

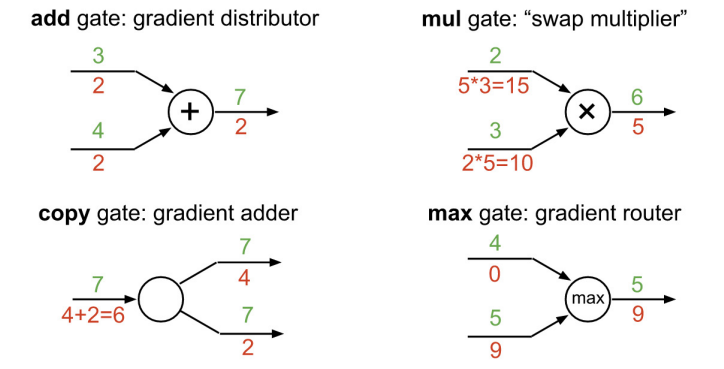
• add 특징 : gradient가 같음
• mul 특징 : w(local gradient)에 upstream gradient를 곱해주면 downstream gradient가 나옴.