Reformer

손기훈·2024년 9월 3일

논문리뷰

목록 보기

2/4

Reformer

제안 배경

트랜스포머에 사용되는 데이터와 모델의 크기를 대략적으로 계산해보자면 트랜스포머 레이어가 대략 2GB 정도 소요하고 embedding크기가 1024인 64K 토큰에 배치 사이즈가 8인 Activations를 계산해보자면 역시 2GB가 소요된다. 또한, 실제로 버트를 파인튜닝하기 위해서는 사용된 데이터가 17GB인 걸 감안하면 한 개의 GPU에서 충분히 올릴 수 있는 크기의 사이즈이다. 하지만 이는 다음과 같은 트랜스포머의 메모리 사용을 감안하지 않은 것이다.
- 레이어의 개수가 N개가 될 때 필요로 하는 메모리 역시 N 배가 된다.
- Feed Forward 레이어의 깊이가 어텐션 activations의 깊이보다 훨씬 크다.
- 어텐션 시퀀스의 연산 복잡도가 $O(L^2)$ 이다.
이는 논문에서 제안하는 다음 세 가지의 기법을 통해서 해결이 가능하다.
- Reversible Layers
- FeedForward Chunking
- LSH attention

메카니즘

LSH Attention

Hashing Attention
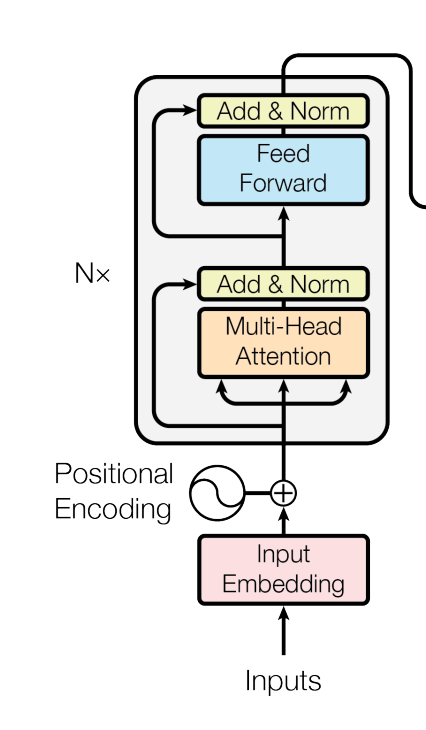
- 트랜스포머가 Q,K,V를 생성하기 위해서는 각각 서로 다른 3개의 선형 레이어를 필요로 하게 된다.
  1. ReFormer에서 LSH 어텐션을 활용하기 위해 Q와 K를 같게 만든다. 이를 위해서는 Q와 K가 동일한 레이어를 통과하면 되므로, 2개의 선형 레이어만을 필요로 하게 된다.
  2. 멀티 헤드 어텐션에서 가장 많은 연산을 사용하는 파트는 QK^T 이므로 이를 memory-efficient attention으로 대체한다. 이는 $softmax(\frac{q_iK^T}{\sqrt d_k})$ 로 만드는 것이다.
  3. 여기서 K 벡터와 가까운 q_i를 만들기 위해서 사용되는 기법이 LSH이다.
Local Sensitive Hashing
- Angular LSH
- $h(x) = arg max([xR; −xR])$
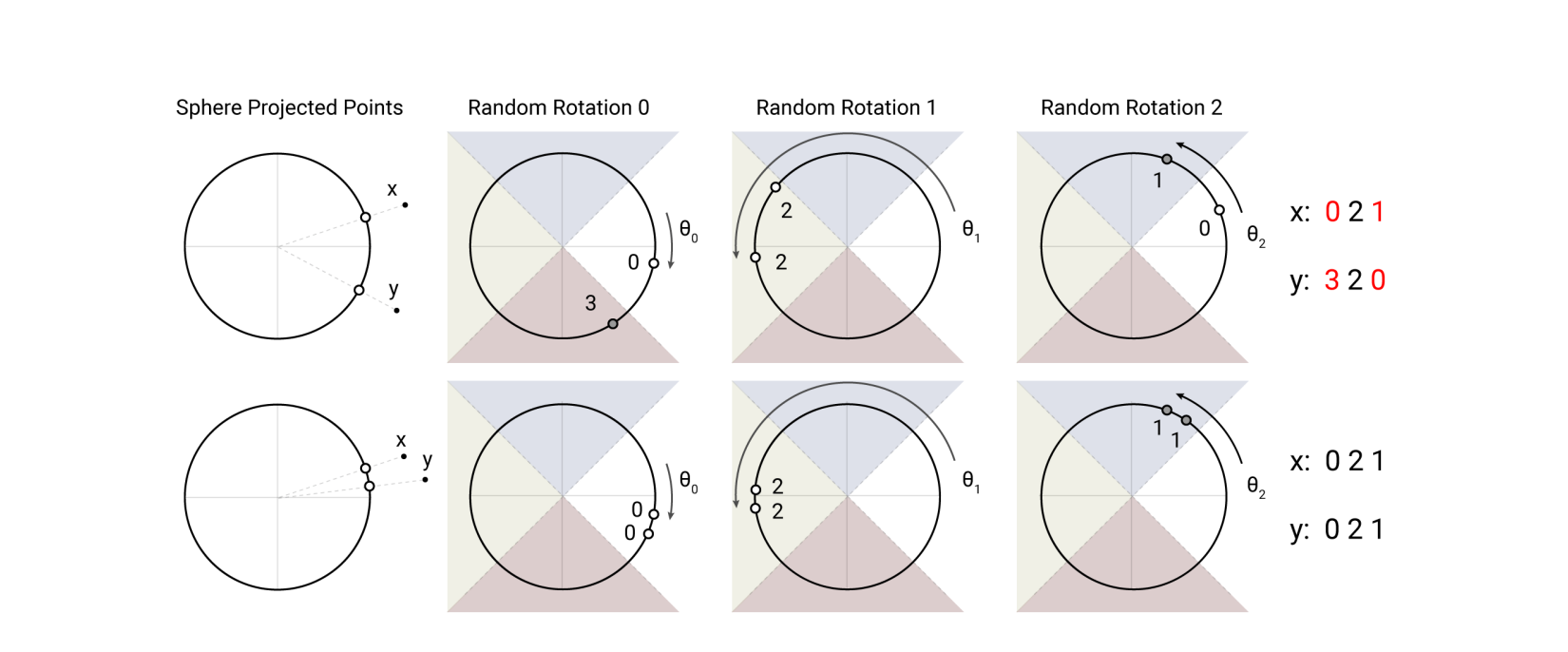
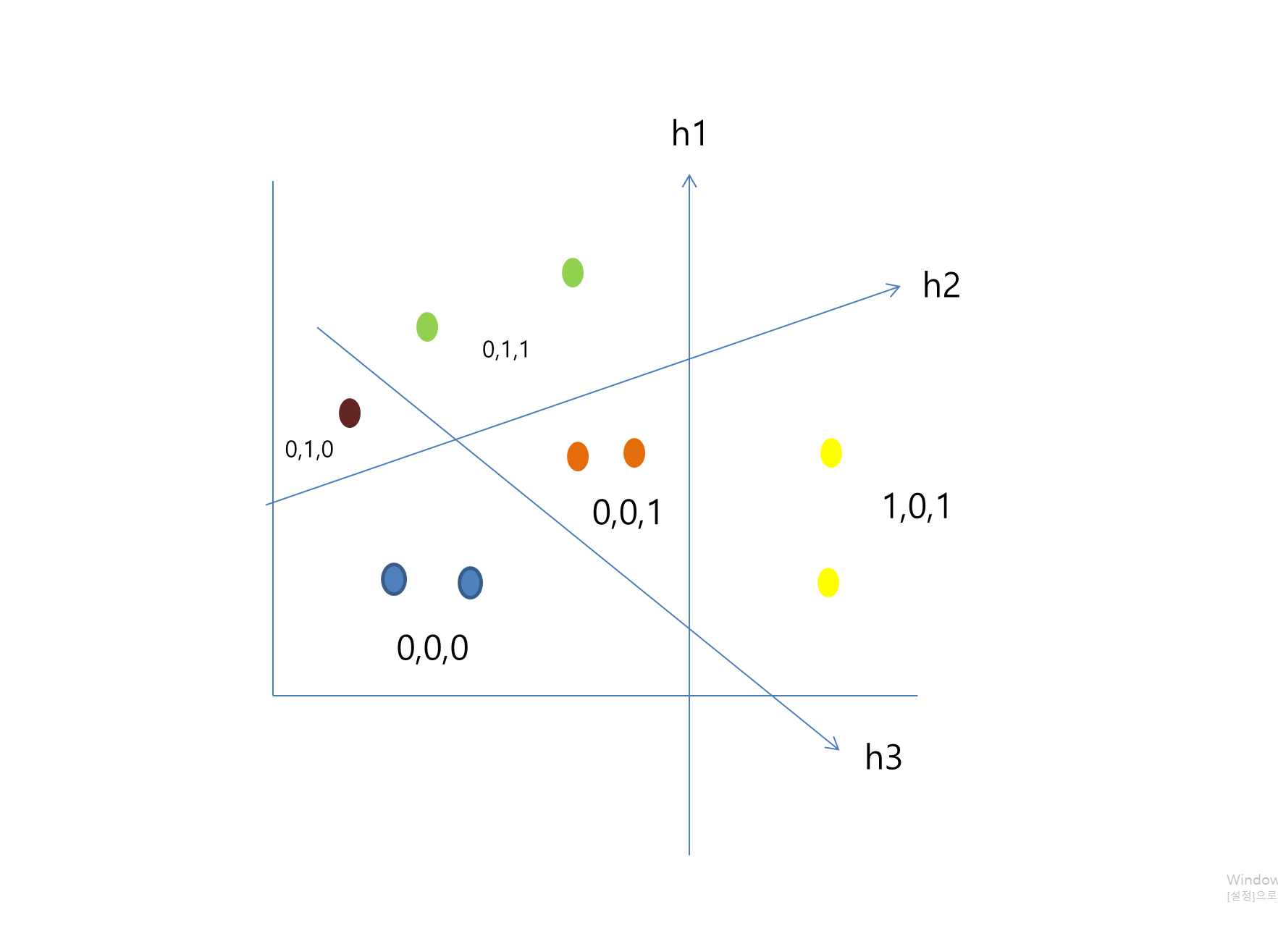
- $R$ 은 랜덤한 $[d_k, b/2]$ 의 행렬 d_k 는 키 벡터의 차원이고 b는 해쉬의 차원이다.
- 벡터 간의 거리가 가까운 벡터에 대해서는 같은 해쉬 함수를 통과했을 때 높은 확률로 같은 해쉬 값을 갖게 되는 해쉬 기법이다.
LSH attention

$o_i = \sum_{j \in P_i} exp(q_i\cdot k_j - z(i, P_i))v_j$

$where P_i = {\{i: i \geq j \}}$
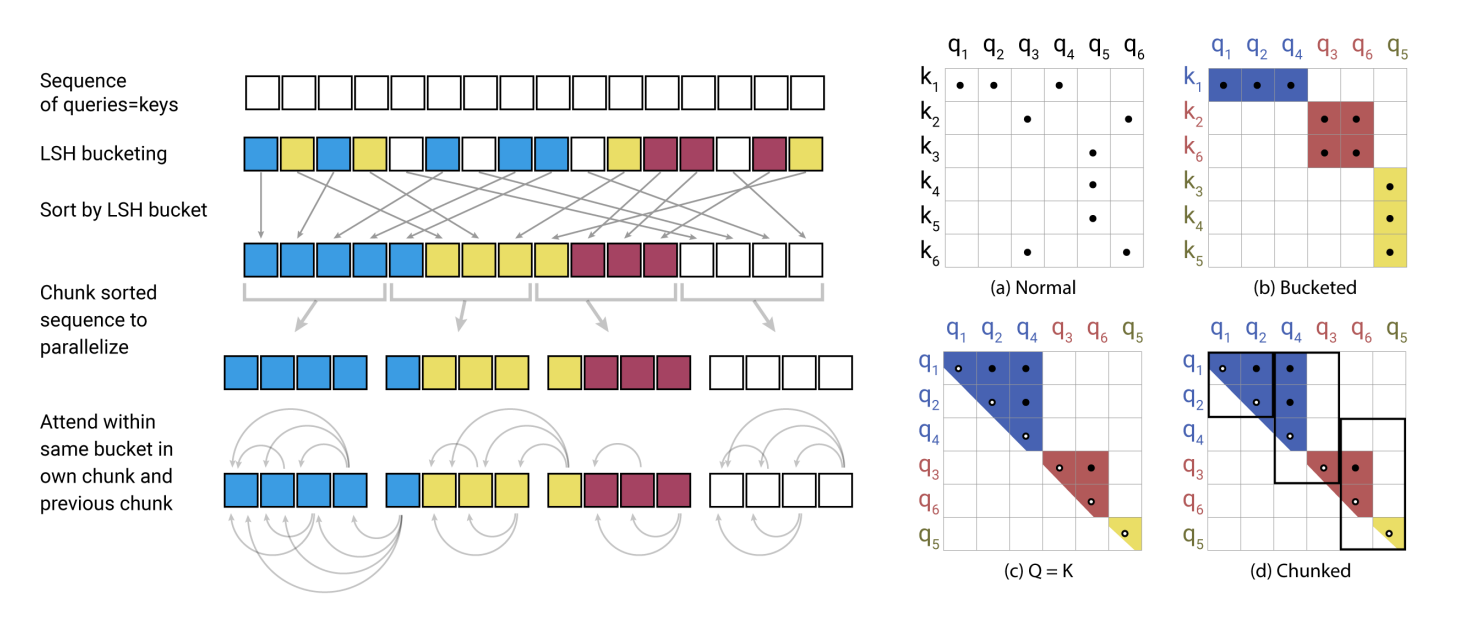
- P_i 는 i번째에 있는 쿼리이다. z는 파티션 함수이거나 노말라이징 함수이다.
1. 키 쿼리 시퀀스를 같은 해쉬 버켓에 넣는다.
2. 해쉬 버켓 넘버에 따라 소팅을 진행한다. 같은 버켓에서는 시퀀스의 순서에 따라
3. 해쉬 버켓을 일정한 청크로 나눈다.
4. 같은 해쉬 버켓에 있는 q_i, 끼리 어텐션을 계산한다. 혹은 바로 앞의 버켓에 있는 경우의 키 토큰에만 진행한다. 이때 자신과 이전의 쿼리에 대해서만 어텐션을 진행한다. ⇒ 극단적인 경우, 모든 토큰이 같은 해쉬 값을 가지고 있을 때 모든 토큰에 대해서 어텐션을 계산할 수도 있기 때문에.
multi-round LSH attention
- 비슷한 거리의 벡터에도 불구하고 때로는 다른 버켓에 떨어지게 되는 경우가 있다. 이를 해결해주기 위해서 여러번의 LSH 어텐션을 진행한다.
- 여러번의 LSH 어텐션을 통과한 후에는 결과를 모두 concat하여 내보낸다.

Reversible Transformer

Reversible Network이란?
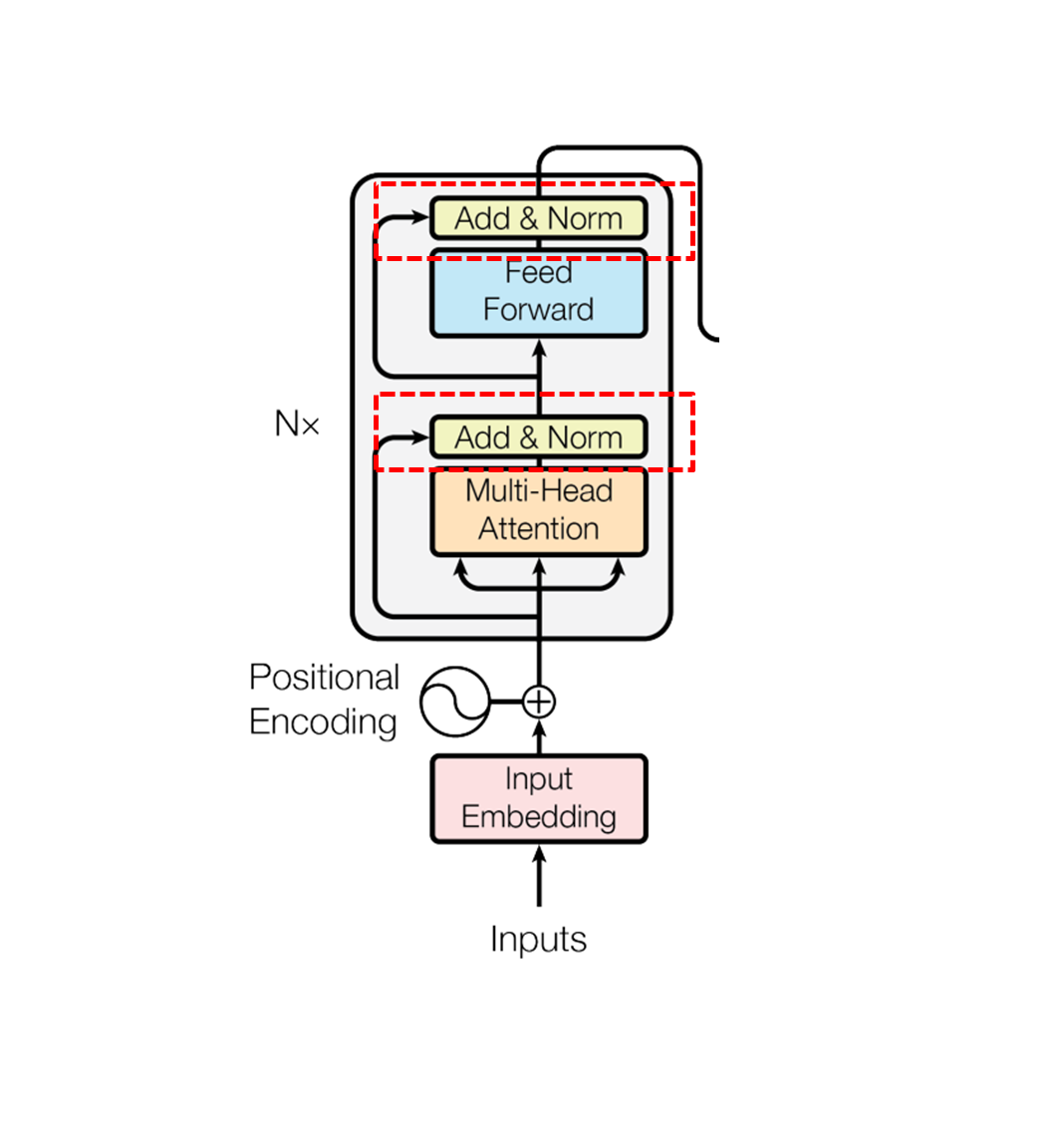
- Residual Network의 단점인, 역전파 시에 중간 결과를 전부 저장하여 메모리가 커지는 문제점을 해결하기 위해서 제안된 모델
  
  $y_1 = F(x_2) + x_1\\y_2 = G(x_1) + x_2$ $x_1 = y_1 - F(x_2)\\x_2 = y_2 - G(x_1)$
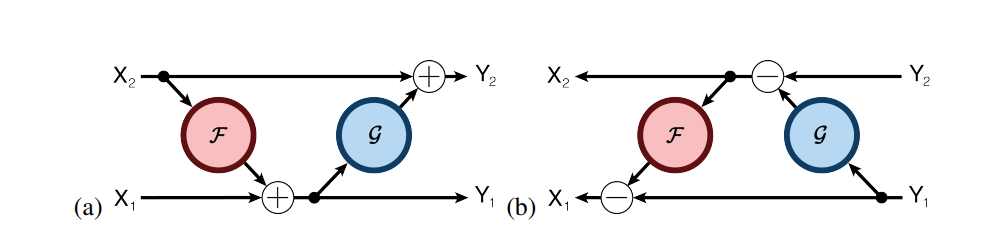
- 위의 식은 Residual Block과 상당히 유사하지만, 바로 input 값을 복원하기 위해 연산을 바로 적용하여 Back Computation이 가능하다는 장점이 있다. 따라서, Residual Block 처럼 중간 결과를 저장할 필요가 없게 된다.
Reversible Transformer
- 입력값 x를 복사하여, Reversible Network를 통과한 결과값 y_1, y_2를 평균값을 내어 결과를 반환한다. $Y_1 = X_1 + Attention(X_2)\\Y_2 = X_2 + FeedForward(Y_1)$

FeedForward Chunking

feedforward 레이어는 멀티헤드 어텐션을 적용하고 나온 결과를 확장해주는 리니어 레이어 1개와 다시 원래 차원으로 축소해주는 리니어 레이어 1개로 총 두개로 이루어져있다. 따라서 매우 연산량이 크다.
하지만, 어텐션과는 다르게 feedforward 레이어는 시퀀스에서 토큰의 위치가 독립적이므로여러개의 청크로 나눠서 계산 될 수 있다.