뉴런과 신경망의 기본 개념
-
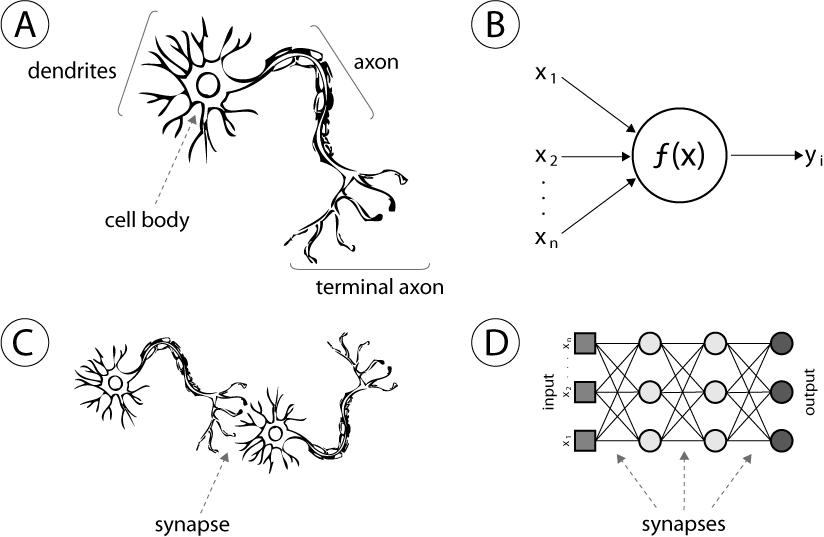
1944년, Warren McCullough와 Walter Pitts가 처음으로 인공 신경망(Neural Network)의 개념을 제안했습니다.
- 이 아이디어는 인간의 뇌가 수많은 신경세포(Neuron) 를 통해 신호를 주고받는 구조를 수학적으로 모방한 것이었습니다.
-
오늘날 이 개념은 여러 층(Layer)의 신경망을 쌓은 딥러닝(Deep Learning) 으로 발전해, 음성 인식, 이미지 분류, 번역 등 다양한 인공지능 응용 기술의 기반이 되고 있습니다.
1. 활성화 함수 (Activation Functions)
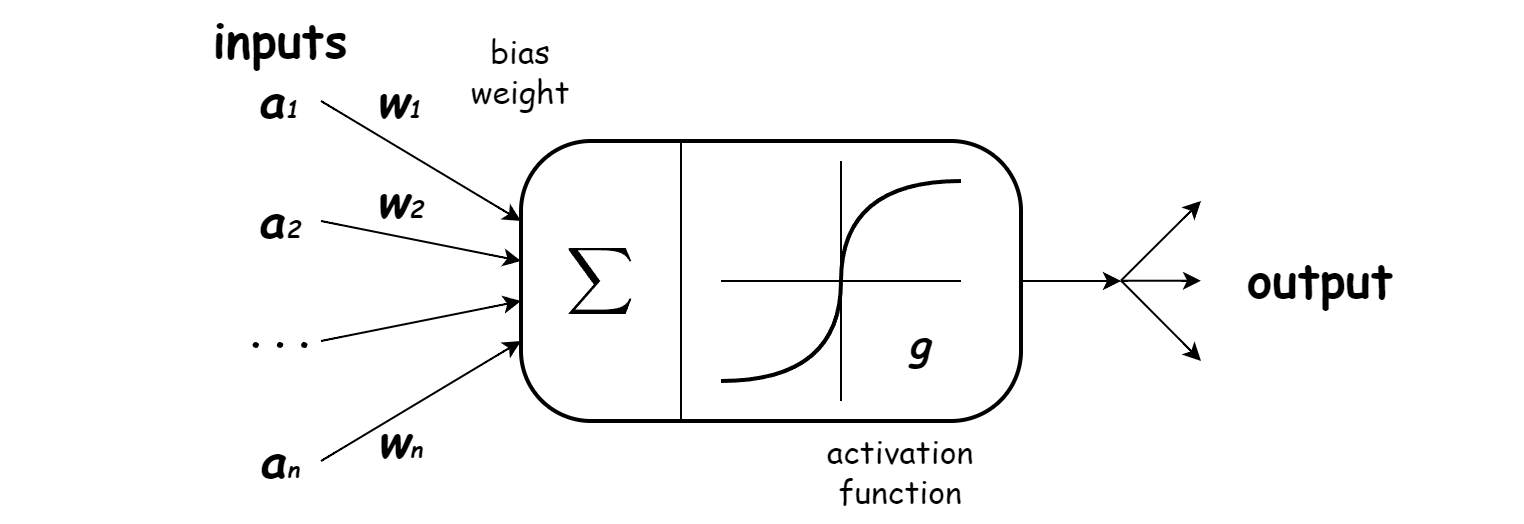
활성화 함수는 아래와 같이 다양한 종류가 있고 신경망을 개발할 때 사람이 선택 가능합니다. 활성화 함수의 선택은 신경망의 예측 성능에 영향을 미칩니다, 논문을 보니 보통은 하나씩 다 해봐서 성능이 좋은것을 선택하는 것 같습니다.

-
마지막 활성화 함수는 전체 뉴럴넷의 출력값을 결정하기 때문에 중요한 의미를 갖습니다.
-
예를 들어 1장에서 말씀드린 회귀문제 예측하기 위한 신경망의 경우 Sigmoid와 같이 0~1사이의 범위만을 갖는 활성화 함수를 사용하면 트레이닝을 아무리 진행해도 오차(Error)가 감소가 되지 않을 것 입니다.
-
일반적으로 이중 분류문제 True(1), False(0)를 예측하는 경우 마지막 레이어의 활성화 함수를 Sigmoid를 사용해서 두개중 어느 클래스에 가까운지 예측합니다.
-
주택가격 예측과 같은 회귀문제의 경우 마지막 퍼셉트론에 활성화 함수를 사용하지 않고 가중합하여 예측값를 계산하거나, ReLU와 같이 값이 무한한 활성화 함수를 사용할 수 있습니다.
-
최소한 활성화 함수 출력 범위내에 라벨값(Y)들이 포함되어 있어야 정상적인 학습이 진행됩니다.
-
활성화 함수(Activation Function)는 뉴런이 입력 신호를 받아 출력 신호로 변환하는 과정에서, 비선형성을 부여하는 수학적 함수이다.
-
신경망(Neural Network)은 본질적으로 입력과 가중치의 선형 결합을 수행하지만, 활성화 함수가 없다면 전체 네트워크는 단일 선형 변환과 다를 바 없게 된다.
- 따라서 비선형 활성화 함수의 도입은 신경망이 복잡한 데이터 패턴과 비선형 경계를 학습할 수 있게 하는 핵심 요소이다.
2. 활성화 함수의 필요성
-
활성화 함수가 없다면 다음과 같은 문제가 발생한다.
-
여러 층을 쌓아도 선형 변환이 반복될 뿐, 결과적으로 하나의 행렬 곱으로 단순화된다.
-
즉, 은닉층이 존재해도 “비선형성”이 없다면 표현력(Representation Power) 이 증가하지 않는다.
사실 딥러닝으로 해결하려는 문제들은 대부분 단순한 문제들이 아닙니다. 굉장히 복잡하고 난잡한 문제들이기 때문에 데이터속에 숨겨저 있는 진짜 회귀 선, 경계면은 입력데이터(X)의 다차원 공간에서 굉장히 해괴한 곡선(비선형)의 모습을 보여줍니다.
- 만약 활성화 함수를 사용하지 않고 입력데이터(X)에 가중합만 이용한다면 복잡하고 유연한 함수를 생성 것이 아니라 데이터의 선형 변형(Transformation)만을 하기 때문에 복잡한 진짜 회귀 선, 경계면에 핏팅하기가 어렵습니다.
-
-
반면, 활성화 함수는 각 층이 다른 비선형 변환을 수행하도록 하여, 네트워크 전체가 “입력 공간에서 고차원적 특징을 단계적으로 학습”할 수 있게 만든다.
-
이로써 신경망은 선형 분리가 불가능한 데이터조차 구분할 수 있다.
3. 좋은 활성화 함수의 조건
-
활성화 함수가 신경망 학습에 적합하려면 다음 성질들을 가지는 것이 이상적이다.
-
비선형성(Non-linearity): 복잡한 함수 근사를 위해 필요
-
연속성과 미분 가능성(Differentiability): 역전파(Backpropagation) 계산을 위해 필요
-
적절한 출력 범위(Boundedness): 출력이 너무 커지거나 작아지는 것을 방지
-
단조성(Monotonicity): 학습의 안정성 확보
-
원점 근처에서의 동일성(Identity near origin): 초기 가중치가 작을 때 효율적 학습 가능
-
4. 주요 활성화 함수의 발전 과정
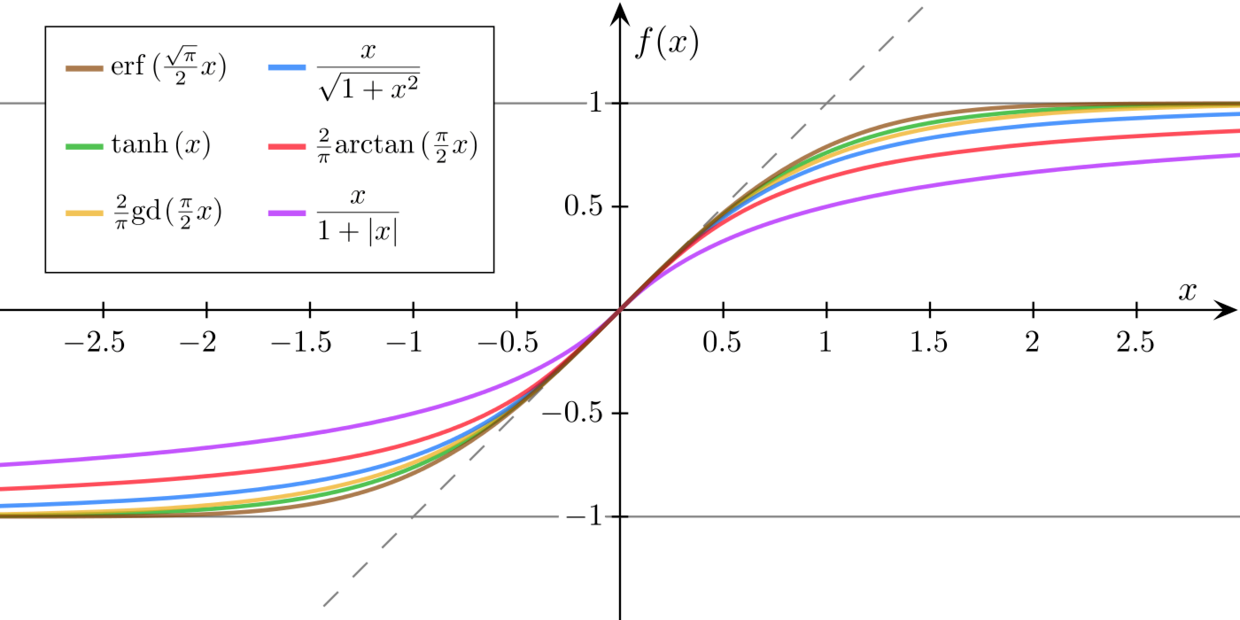
1) Sigmoid Function
-
초기 신경망에서 가장 널리 사용된 함수로, 출력 범위가 (0, 1)이다.
-
뉴런의 출력을 확률로 해석할 수 있다는 장점이 있다.
-
그러나 깊은 네트워크에서는 기울기 소실(Vanishing Gradient) 현상이 심각하게 발생한다.
-
-
장점: 단순하며 직관적 확률 해석 가능
-
단점: 출력이 0 중심이 아니고, 기울기가 작아지면서 학습이 정체됨
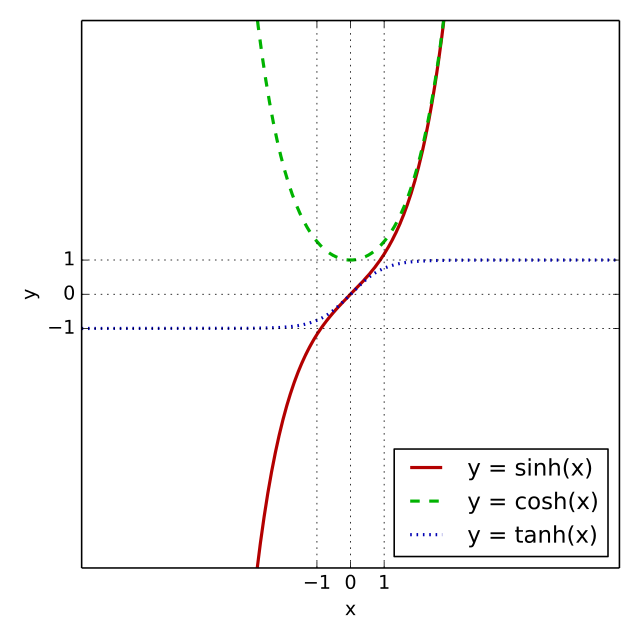
2) Hyperbolic Tangent (tanh)
-
Sigmoid의 단점을 보완한 형태로, 출력 범위가 (-1, 1)이다.
- 입출력의 평균이 0에 가까워 학습 속도는 개선되지만, 여전히 기울기 소실은 남아 있다.
-
장점: Zero-centered, Sigmoid보다 안정적
-
단점: 여전히 깊은 층에서는 기울기 문제 존재
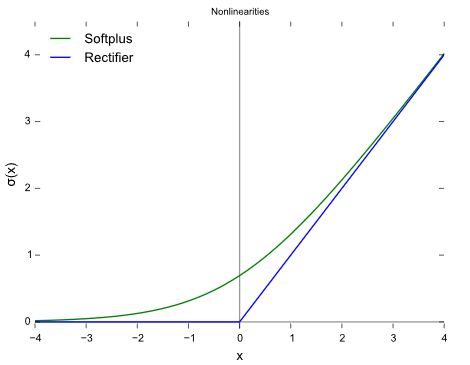
3) ReLU (Rectified Linear Unit)
-
현재 가장 널리 사용되는 활성화 함수이다.
-
입력이 0보다 작으면 0, 크면 그대로 통과시킨다.
-
단순한 형태지만 학습 속도가 빠르고, 기울기 소실 문제가 대폭 줄어든다.
-
장점
-
계산 효율 높음 (비교만으로 구현 가능)
-
기울기 소실 문제 완화
-
희소 활성화(Sparse Activation)로 연산 효율 향상
-
-
단점
- 입력이 음수일 경우 gradient가 0이 되어 뉴런이 영구적으로 “죽는” 현상 발생 (Dying ReLU 문제)
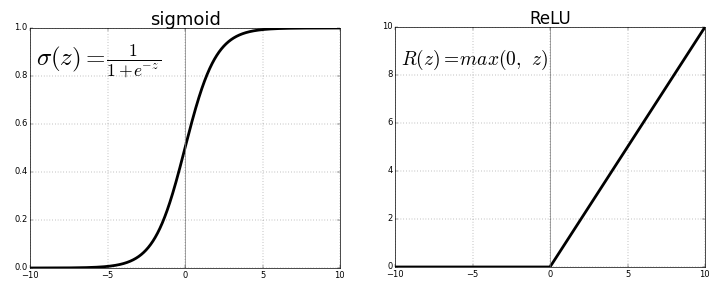
4) Leaky ReLU
-
ReLU의 단점을 보완하기 위해 고안된 함수
-
음수 영역에도 작은 기울기를 허용하여 뉴런이 완전히 죽지 않도록 한다.
-
장점: Dying ReLU 완화
-
단점: α 값이 고정되어 학습 데이터에 따라 최적이 아닐 수 있음
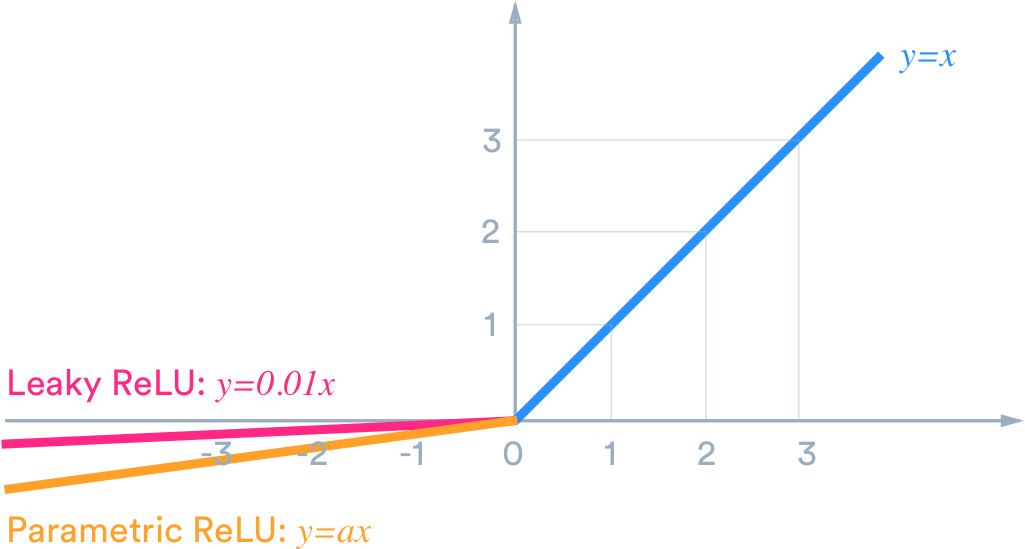
5) Parametric ReLU (PReLU)
-
Leaky ReLU의 α 값을 학습 가능한 파라미터로 바꾼 형태.
- 즉, 음수 구간의 기울기(a)를 데이터 기반으로 자동 조정한다.
-
장점: 데이터 특성에 맞춰 음수 기울기를 최적화
-
단점: 학습 파라미터 증가로 모델 복잡도 상승
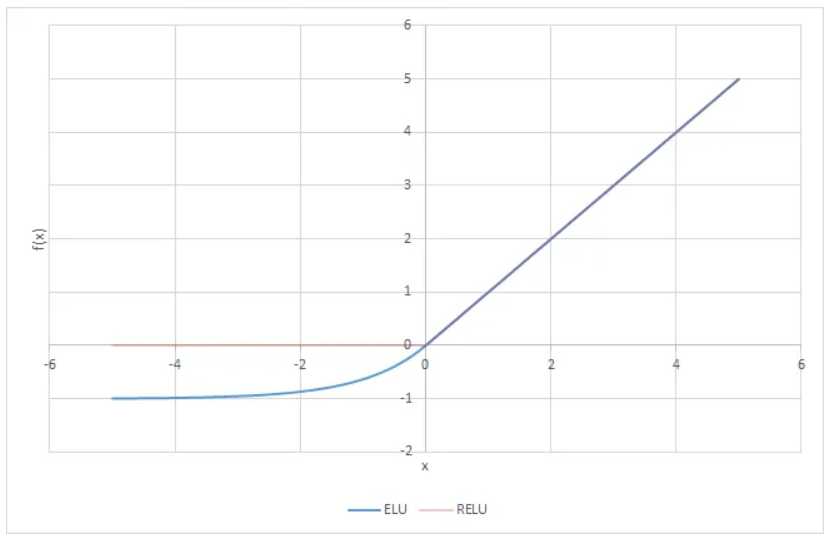
6) ELU (Exponential Linear Unit)
-
지수 형태의 완만한 곡선을 가지며, 평균 활성화를 0에 가깝게 유지한다.
-
ReLU보다 부드럽게 동작하고, 수렴 속도가 빠르다.
-
장점: 0 평균 유지 → 학습 안정성 향상
-
단점: 지수 연산으로 계산 비용 증가
7) Threshold ReLU (TReLU)
-
ReLU와 유사하지만, 임계값(Threshold) 을 추가한 형태이다.
-
입력이 일정 임계값(θ)보다 클 때만 활성화되며, 작은 음수 입력도 부분적으로 통과시킬 수 있다.
-
장점: ReLU보다 세밀한 활성 제어 가능
-
단점: 파라미터 θ, α 설정이 복잡함
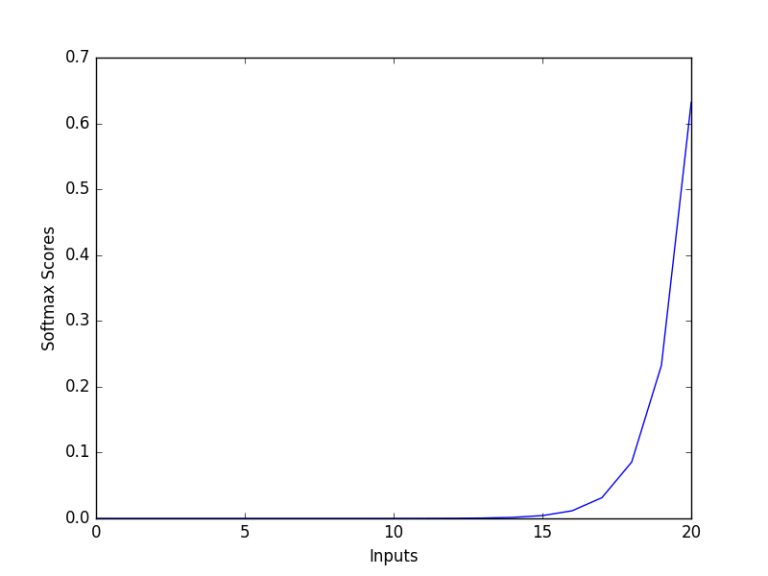
8) Softmax Function
-
출력층에서 자주 사용되는 함수
-
모든 출력을 [0, 1] 범위의 확률 분포로 변환한다.
-
다중 클래스 분류(Multiclass Classification)에 필수적이다.
-
장점: 확률 해석 가능, 다중 클래스 문제에 적합
-
단점: 입력이 큰 경우 overflow 방지를 위한 정규화 필요
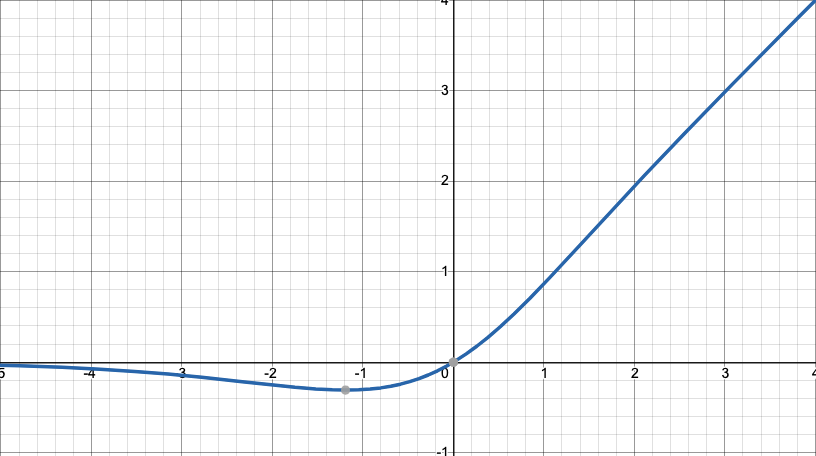
9) Mish Function
-
2019년에 제안된 새로운 활성화 함수로, ReLU 이후 세대의 대표적 비선형 함수이다.
-
Swish 함수와 유사하지만 더 부드럽고, ReLU나 Leaky ReLU에서 발생하던 “죽은 뉴런” 문제를 근본적으로 완화한다.
-
장점
-
Non-monotonic → 음수 값 일부 유지, 정보 손실 완화
-
Unbounded above, bounded below → 포화 방지 및 정규화 효과
-
부드러운 미분 특성으로 일반화 능력 향상
-
YOLOv4, EfficientNet 등에서 실제 정확도 개선
-
-
단점
- 계산량 많음 (log, tanh, exp 연산 포함)
5. 요약 및 비교
| 함수 | 출력 범위 | 주요 특징 | 장점 | 단점 |
|---|---|---|---|---|
| Sigmoid | (0, 1) | S자형 곡선 | 확률적 해석 가능 | 기울기 소실, 0 중심 아님 |
| Tanh | (-1, 1) | 대칭 S자형 | Zero-centered | 여전히 소실 존재 |
| ReLU | [0, ∞) | 절단형 | 빠르고 효율적 | Dying ReLU 발생 |
| Leaky ReLU | (-∞, ∞) | 음수 기울기 추가 | Dying 완화 | α 고정 |
| PReLU | (-∞, ∞) | 학습형 음수 기울기 | 데이터 적응형 | 복잡도 증가 |
| ELU | (-α, ∞) | 지수형 완화 | 0 평균 유지 | 계산량 많음 |
| TReLU | 제한적 | 임계값 적용형 | 세밀 제어 가능 | 파라미터 조정 필요 |
| Softmax | (0, 1), 합=1 | 확률 분포 | 다중 분류용 | Overflow 가능 |
| Mish | (-0.31, ∞) | 부드러운 비단조형 | 표현력·정확도 향상 | 계산량 높음 |
6. 결론
-
활성화 함수는 단순히 “출력을 변환하는 도구”가 아니라, 신경망이 학습할 수 있는 세계의 복잡도를 결정하는 핵심 설계 요소이다.
-
ReLU는 단순성과 속도로 표준이 되었지만, Leaky ReLU, PReLU, ELU 등은 그 한계를 보완한 발전형이다.
-
Mish는 이 계보의 최신 함수로, 부드러움과 안정성을 동시에 제공한다.
-
결국 활성화 함수의 선택은 문제의 특성(데이터, 모델 구조, 손실 함수) 에 따라 달라지며, 현대의 딥러닝에서는 ReLU 계열과 Mish가 가장 널리 쓰인다.
