신경망(Neural Network): 신경망의 기본 구조

신경망(Neural Network)

• 신경망은 인간의 뇌가 수많은 신경세포(뉴런) 들이 서로 연결되어 정보를 주고받는 구조를 모방한 수학적 모델입니다.

• 뉴런들은 입력 신호를 받아 가중치(Weight) 를 적용한 후, 활성화 함수(Activation Function) 에 따라 출력을 계산하고 다음 층으로 전달합니다.

  • 즉, 신경망은 노드(뉴런)들을 계층적으로 연결한 거대한 네트워크이며, 노드들의 연결 방식에 따라 다양한 형태의 신경망이 존재합니다.

2. 신경망의 계층 구조

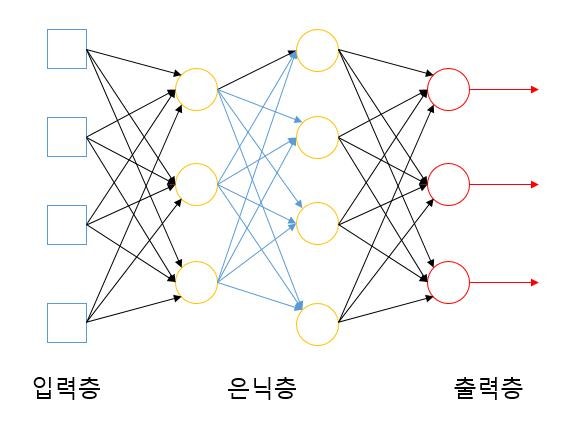
1) 입력층 (Input Layer)

• 입력 데이터를 받는 창구 역할을 합니다.

• 입력층의 노드는 단순히 데이터를 전달할 뿐, 가중합이나 활성화 함수를 적용하지 않습니다.

2) 은닉층 (Hidden Layer)

• 입력층과 출력층 사이에 존재하는 계층입니다.

• 신경망의 외부에서는 직접 접근할 수 없기 때문에 ‘은닉층’이라 불립니다.

• 실제로 가중합 계산과 활성화 함수 적용이 이루어지는 핵심 부분입니다.

3) 출력층 (Output Layer)

• 신경망의 최종 결과값을 출력하는 계층입니다.

• 회귀 문제에서는 선형함수, 분류 문제에서는 Softmax나 Sigmoid 등의 활성화 함수를 사용합니다.

3. 신경망의 종류

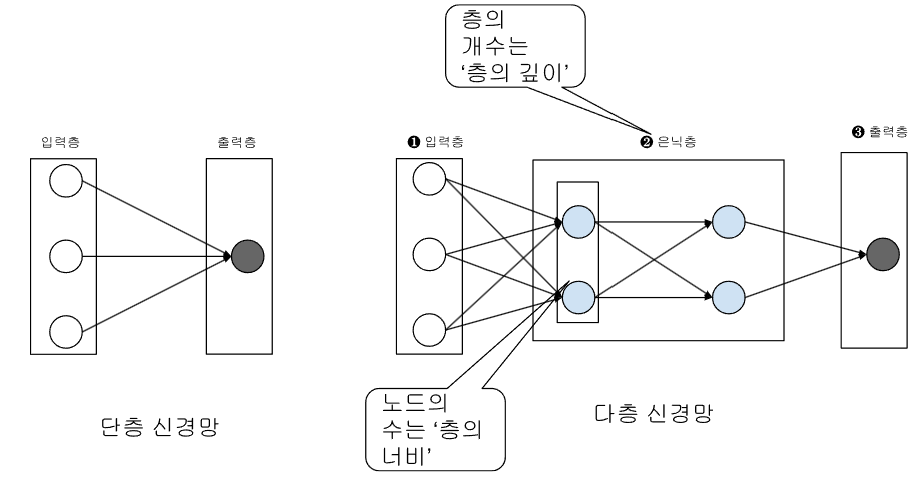
구분	구성	특징
단층 신경망	입력층 - 출력층	가장 단순한 형태
다층 신경망	입력층 - 은닉층(1개) - 출력층	복잡한 패턴을 학습 가능
심층 신경망 (DNN)	입력층 - 은닉층(2개 이상) - 출력층	현대 딥러닝의 기본 구조

• 신경망은 단층 구조에서 시작해 은닉층이 추가되며 복잡도가 증가했습니다.

• 2000년대 중반부터 심층 신경망(Deep Neural Network) 이 등장하면서, 기존의 단층·얕은 신경망과 구분하기 위해 “은닉층이 두 개 이상인 네트워크”를 ‘심층 신경망’이라 부르게 되었습니다.

4. 신호의 흐름 (Forward Propagation)

• 계층형 신경망에서 신호는 다음과 같은 흐름으로 전달됩니다.
  입력층 → 은닉층(가중합 계산 + 활성화 함수) → 출력층
  

• 같은 층의 노드들은 동시에 신호를 입력받고, 처리한 결과를 동시에 다음 층으로 전달합니다.
  

• 이 과정이 바로 순전파(Forward Pass) 입니다.

5. 수학적 표현

• 하나의 노드 계산은 다음과 같습니다.

  $v = W \cdot x + b$
  $y = \rho(v)$

  • $x$: 입력 벡터

  • $W$: 가중치 행렬

  • $b$: 바이어스 벡터

  • $\rho$: 활성화 함수 (예: ReLU, Sigmoid 등)

• 이를 계층 단위로 적용하면 전체 신경망의 순전파 계산을 수식으로 표현할 수 있습니다.

예시: 입력 2 – 은닉 2 – 출력 2 신경망의 행렬 표현

(1) 구조 요약

• 입력층: 2개 노드 (x₁, x₂)

• 은닉층: 2개 노드 (h₁, h₂)

• 출력층: 2개 노드 (y₁, y₂)

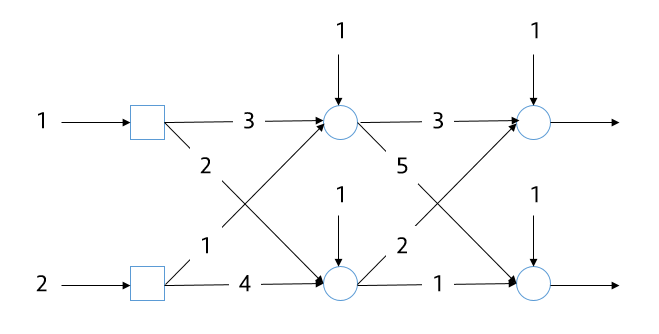
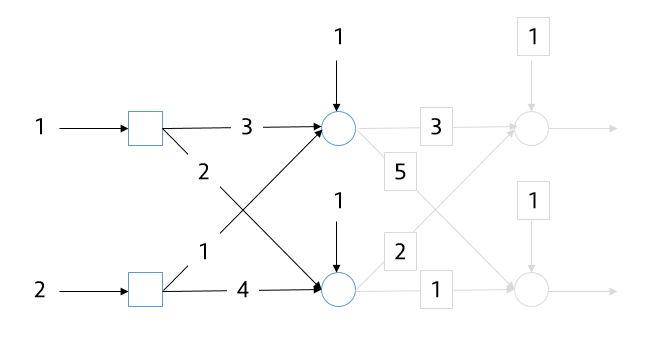
(2) 입력 → 은닉층 가중치 행렬3

그림에서 주어진 가중치 관계는 다음과 같습니다.

연결	가중치
x₁ → h₁	3
x₂ → h₁	1
x₁ → h₂	2
x₂ → h₂	4

따라서 가중치 행렬과 바이어스 벡터는

(3) 은닉 → 출력층 가중치 행렬

연결	가중치
h₁ → y₁	3
h₂ → y₁	2
h₁ → y₂	5
h₂ → y₂	1

이에 따라

(4) 순전파 식

입력 벡터를

이라 하면 전체 연산은 다음과 같습니다.

즉,

(5) 실제 예시 계산

입력을

이라고 하면,

1. 은닉층 계산

2. 출력층 계산

따라서 최종 출력은

(6) 형태 요약

항목	기호	크기
입력 벡터	x	(2×1)
입력 → 은닉 가중치	W₁	(2×2)
은닉층 바이어스	b₁	(2×1)
은닉 → 출력 가중치	W₂	(2×2)
출력층 바이어스	b₂	(2×1)
출력 벡터	y	(2×1)

이 구조는 그림에서 보인 모든 대각선 및 교차 가중치 연결을 포함한 완전 연결(fully connected) 신경망입니다.

6. 활성화 함수의 필요성

• 만약 활성화 함수를 선형 함수로만 사용하면, 은닉층을 여러 개 추가하더라도 결과적으로 단층 신경망과 동일한 효과만 얻습니다.

  • 즉, 다음과 같은 관계가 성립합니다.

    $y = W_2 (W_1 x + b_1) + b_2 = (W_2 W_1) x + (W_2 b_1 + b_2)$

• 이처럼 선형함수만 사용하면 두 층을 하나로 “접을 수” 있습니다.

  • 따라서 비선형 활성화 함수(ReLU, Sigmoid 등) 가 반드시 필요합니다.

7. 순전파 계산 예시 (Python)

• 아래 코드는 위의 개념을 그대로 구현한 간단한 예제입니다.

• 은닉층이 한 개인 신경망을 만들고, 선형 활성함수를 사용할 때와 ReLU를 사용할 때의 차이를 비교합니다.

import numpy as np

def forward(x, W1, b1, W2, b2, activation="linear"):
    v1 = W1 @ x + b1
    if activation == "linear":
        h = v1
    elif activation == "relu":
        h = np.maximum(0, v1)
    else:
        raise ValueError("activation must be 'linear' or 'relu'")
    v2 = W2 @ h + b2
    return h, v2

def collapse_linear_two_layers(W1, b1, W2, b2):
    W_eq = W2 @ W1
    b_eq = W2 @ b1 + b2
    return W_eq, b_eq

x  = np.array([1.0, 2.0])
W1 = np.array([[3.0, 1.0],
               [2.0, 4.0]])
b1 = np.array([1.0, 1.0])
W2 = np.array([[1.0, 1.0]])
b2 = np.array([0.0])

print("=== 순전파: 선형 활성 ===")
h_lin, y_lin = forward(x, W1, b1, W2, b2, activation="linear")
print("입력:", x)
print("은닉층 출력:", h_lin)
print("출력층 출력:", y_lin)

W_eq, b_eq = collapse_linear_two_layers(W1, b1, W2, b2)
y_eq = W_eq @ x + b_eq
print("\n=== 등가 단층 계산 ===")
print("W_eq =", W_eq)
print("b_eq =", b_eq)
print("y_eq =", y_eq)

print("\n=== 순전파: ReLU 활성 ===")
h_relu, y_relu = forward(x, W1, b1, W2, b2, activation="relu")
print("은닉층 출력(ReLU):", h_relu)
print("출력층 출력(ReLU):", y_relu)

실행 결과 예시

=== 순전파: 선형 활성 ===
입력: [1. 2.]
은닉층 출력: [ 6. 11.]
출력층 출력: [17.]

=== 등가 단층 계산 ===
W_eq = [[5. 5.]]
b_eq = [2.]
y_eq = [17.]

=== 순전파: ReLU 활성 ===
은닉층 출력(ReLU): [ 6. 11.]
출력층 출력(ReLU): [17.]

• 선형 활성(linear) 은 두 층을 하나로 합쳐도 결과가 동일함을 보입니다.

• ReLU 활성(ReLU) 을 쓰면 더 이상 선형 결합으로 단층으로 표현할 수 없습니다.

8. 정리

• 신경망은 입력층 – 은닉층 – 출력층으로 구성된 계층적 네트워크이다.

• 은닉층이 많을수록 복잡한 비선형 관계를 학습할 수 있다.

• 활성화 함수가 선형이면 계층을 추가해도 의미가 없다.

• 현대의 대부분의 신경망(딥러닝 모델)은 심층 신경망(Deep Neural Network) 구조를 사용한다.