노름(Norm)

노름(Norm) 이란?

• 노름(Norm)은 벡터나 행렬의 크기(길이 혹은 크기)를 측정하는 값입니다.

• 수학적으로, 노름은 벡터 공간에서 특정 벡터가 원점(제로 벡터)에서 얼마나 "멀리" 떨어져 있는지 나타냅니다.

• 노름은 벡터의 크기(= 거리 측정)를 특정 방식으로 나타내는 함수이며, 다양한 방식으로 계산할 수 있습니다.

표준 조건

• 노름 ($||\mathbf{v}||$)은 아래 조건을 만족해야 합니다.

1. 양의 정부호성

   • ($||\mathbf{v}|| \geq 0$) (항상 0 이상).

   • ($||\mathbf{v}|| = 0$) 은 $\mathbf{v}$가 영벡터일 때에만 성립.

2. 균등성

   • ($||c\mathbf{v}|| = |c| \cdot ||\mathbf{v}||$): 벡터 크기를 상수배하면, 노름은 상수의 절댓값만큼 변화.

3. 삼각 부등식

   • ($||\mathbf{u} + \mathbf{v}|| \leq ||\mathbf{u}|| + ||\mathbf{v}||$): 두 벡터의 합의 크기는 각각의 크기의 합보다 크지 않음.

4. 영벡터의 크기

   • ($||\mathbf{0}|| = 0$): 영벡터의 노름은 항상 0.

주요 노름 종류

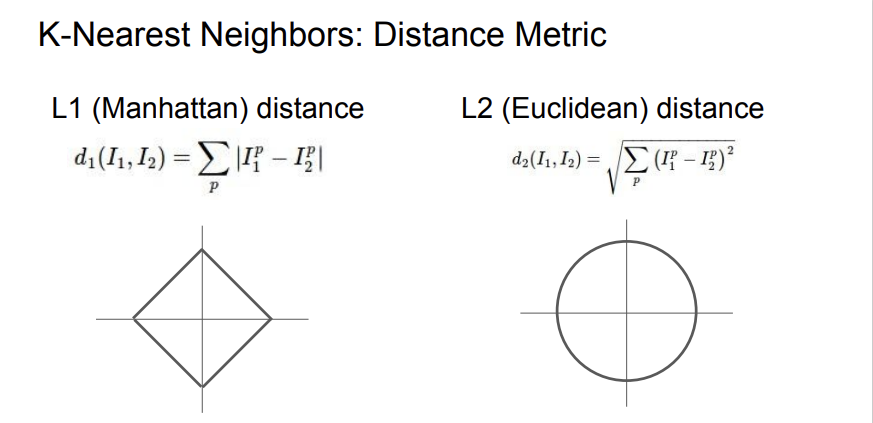
(1) $\ell_1$ 노름 (맨해튼 노름, Manhattan Norm)

• 벡터 각 성분의 절댓값의 합.

  $||\mathbf{v}||_1 = \sum_{i=1}^n |v_i|$

• 특징

  • 맨해튼 거리라고도 하며, 도시의 직각 거리를 측정하는 방식에서 이름이 유래.

  • 이상치(outlier)에 둔감.

• 활용 예: 데이터를 희소하게 만들거나(sparse 모델링) 이상치가 있는 경우.

(2) $\ell_2$ 노름 (유클리드 노름, Euclidean Norm)

• 벡터 성분의 제곱합의 제곱근.

  $||\mathbf{v}||_2 = \sqrt{\sum_{i=1}^n v_i^2}$

• 특징

  • 공학과 물리에서 직관적인 유클리디안 거리(유클리드 거리)를 나타냄.

  • 모든 성분 크기를 고르게 반영하며, 이상치에 민감.

• 활용 예: 선형 회귀, 거리 기반 알고리즘(예: K-최근접 이웃(KNN)).

(3) $\ell_\infty$ 노름 (최대 노름, Maximum Norm)

• 정의: 벡터에서 성분 값의 최대 절댓값.

  $||\mathbf{v}||_\infty = \max_i |v_i|$

• 특징

  • 벡터에서 "가장 큰 절댓값"만을 반영.

  • 계산 비용이 적음.

• 활용 예: 컴퓨팅 성능을 향상시키기 위해 간단한 계산 필요시 사용.

(4) 일반화된 $\ell_p$ 노름

• 정의

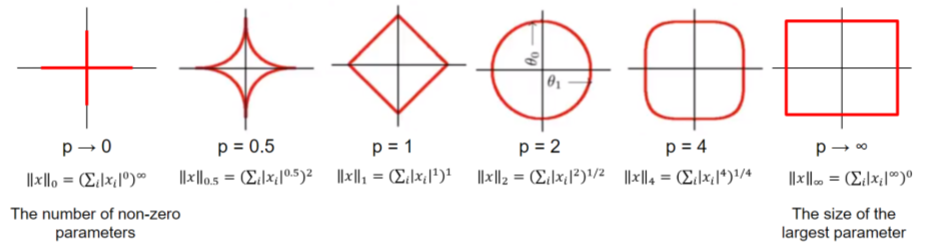
  $||\mathbf{v}||_p = \left( \sum_{i=1}^n |v_i|^p \right)^{1/p}$

  • ( p = 1 ), ( p = 2 ), ( p = \infty )는 각각 ($\ell_1$), ($\ell_2$), ($\ell_\infty$) 를 의미.

  • ( p )가 증가할수록 큰 성분에 더 많은 가중치를 둠.

• 특징

  • 일반화를 통해 다양한 상황에서 거리 또는 크기를 측정.

노름의 활용

1. 거리 계산

   • 벡터 간의 거리 측정 방식에 따라 노름을 선택.

   • $\ell_2$ 노름은 유클리드 거리, $\ell_1$ 노름은 맨해튼 거리로 활용.

2. 모델 정규화(Regularization)

   • 머신러닝에서 과적합을 방지하기 위해 $\ell_1$ 또는 $\ell_2$ 노름을 정규화 항으로 사용.

   • $\ell_1$ 정규화: 희소 모델 생성(Lasso).

   • $\ell_2$ 정규화: 모델 가중치 크기 최소화(Ridge).

3. 안정성 평가

   • 숫자나 매트릭스 크기의 안정성을 측정.

요약 표

노름 종류	정의	특징	활용
$\ell_1$ 노름	성분의 절댓값의 합	이상치에 둔감, 희소 모델 활용	선형 회귀(Lasso), 이상치 처리
$\ell_2$ 노름	성분 제곱의 합의 제곱근	유클리드 거리, 이상치에 민감	선형 회귀(Ridge), KNN 등
$\ell_\infty$ 노름	성분 절댓값 중 최대값	계산 비용 적음	단순 계산, 최댓값 기반 분석
$\ell_p$ 노름	성분 절댓값의 ( p )제곱의 합의 ( 1/p )승	$\ell_1$, $\ell_2$, $\ell_\infty$ 로 확장 가능	다양한 거리 기반 계산