오차 지표 설명: MSE, RMSE, MAE

참고

언제 MSE, MAE, RMSE를 사용하는가?

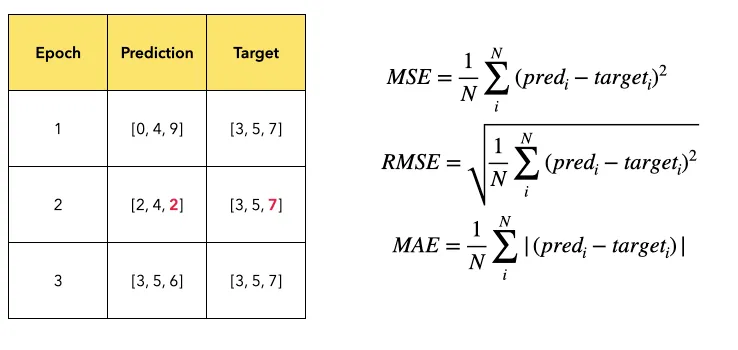
• 어떤 모델이 학습 데이터를 입력받아 아래 테이블 내 수치들을 예측했다고 해보자.

  • target은 prediction이 맞춰야 할 정답이고, epoch은 학습의 횟수를 가리킨다.

  • Epoch 2에서, Prediction의 3번째 값인 2는 그것이 근접했어야 할 Target의 3번째 값인 7과 크게 벗어나게 예측했다는 의미에서 Outlier라는 점에 주목하자.

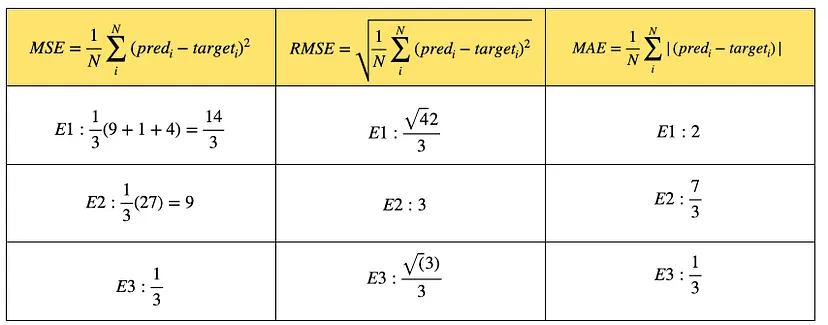
• 이들 값을 가지고 MSE, RMSE, MAE를 계산해보면 아래와 같다.

• jupyter notebook 실행

cd ml
.\env\Scripts\activate
jupyter notebook

• 실행 코드

import numpy as np

def MSE(pred, target, epochs=None):
    if epochs is None:
        epochs = len(pred)  # 함수 내부에서 pred 길이를 설정
    losses = []
    for i in range(epochs):
        losses.append(np.sum((pred[i] - target[i])**2) / len(pred[i]))
    return losses

def RMSE(pred, target, epochs=None):
    if epochs is None:
        epochs = len(pred)
    losses = []
    for i in range(epochs):
        losses.append(np.sqrt(np.sum((pred[i] - target[i])**2) / len(pred[i])))
    return losses

def MAE(pred, target, epochs=None):
    if epochs is None:
        epochs = len(pred)
    losses = []
    for i in range(epochs):
        losses.append(np.sum(np.abs(pred[i] - target[i])) / len(pred[i]))
    return losses

# 입력 데이터
pred = np.array([[0, 4, 9], [2, 4, 2], [3, 5, 6]])
target = np.array([[3, 5, 7], [3, 5, 7], [3, 5, 7]])

# 함수 호출
print("MSE:", MSE(pred, target))
print("RMSE:", RMSE(pred, target))
print("MAE:", MAE(pred, target))

• 개선 코드

  • len(pred)와 len(pred[i])

    • len(pred)는 전체 배열의 행 개수, len(pred[i])는 각 행의 열 개수입니다. 여기서는 len(pred[i])로 계산해야 맞습니다.

  • epochs와 데이터 길이 체크

    • epochs가 데이터보다 클 경우, 이를 처리하기 위해 min(epochs, len(pred))를 사용하는 것이 좋습니다.

import numpy as np

def MSE(pred, target, epochs=None):
    if epochs is None:
        epochs = len(pred)
    losses = []
    for i in range(min(epochs, len(pred))):  # epochs와 pred 길이 중 작은 값 사용
        losses.append(np.sum((pred[i] - target[i])**2) / len(pred[i]))
    return losses

def RMSE(pred, target, epochs=None):
    if epochs is None:
        epochs = len(pred)
    losses = []
    for i in range(min(epochs, len(pred))):
        losses.append(np.sqrt(np.sum((pred[i] - target[i])**2) / len(pred[i])))
    return losses

def MAE(pred, target, epochs=None):
    if epochs is None:
        epochs = len(pred)
    losses = []
    for i in range(min(epochs, len(pred))):
        losses.append(np.sum(np.abs(pred[i] - target[i])) / len(pred[i]))
    return losses

# 입력 데이터
pred = np.array([[0, 4, 9], [2, 4, 2], [3, 5, 6]])
target = np.array([[3, 5, 7], [3, 5, 7], [3, 5, 7]])

# 함수 호출
print("MSE:", MSE(pred, target))
print("RMSE:", RMSE(pred, target))
print("MAE:", MAE(pred, target))

• 결과

MSE: [np.float64(4.666666666666667), np.float64(9.0), np.float64(0.3333333333333333)]
RMSE: [np.float64(2.160246899469287), np.float64(3.0), np.float64(0.5773502691896257)]
MAE: [np.float64(2.0), np.float64(2.3333333333333335), np.float64(0.3333333333333333)]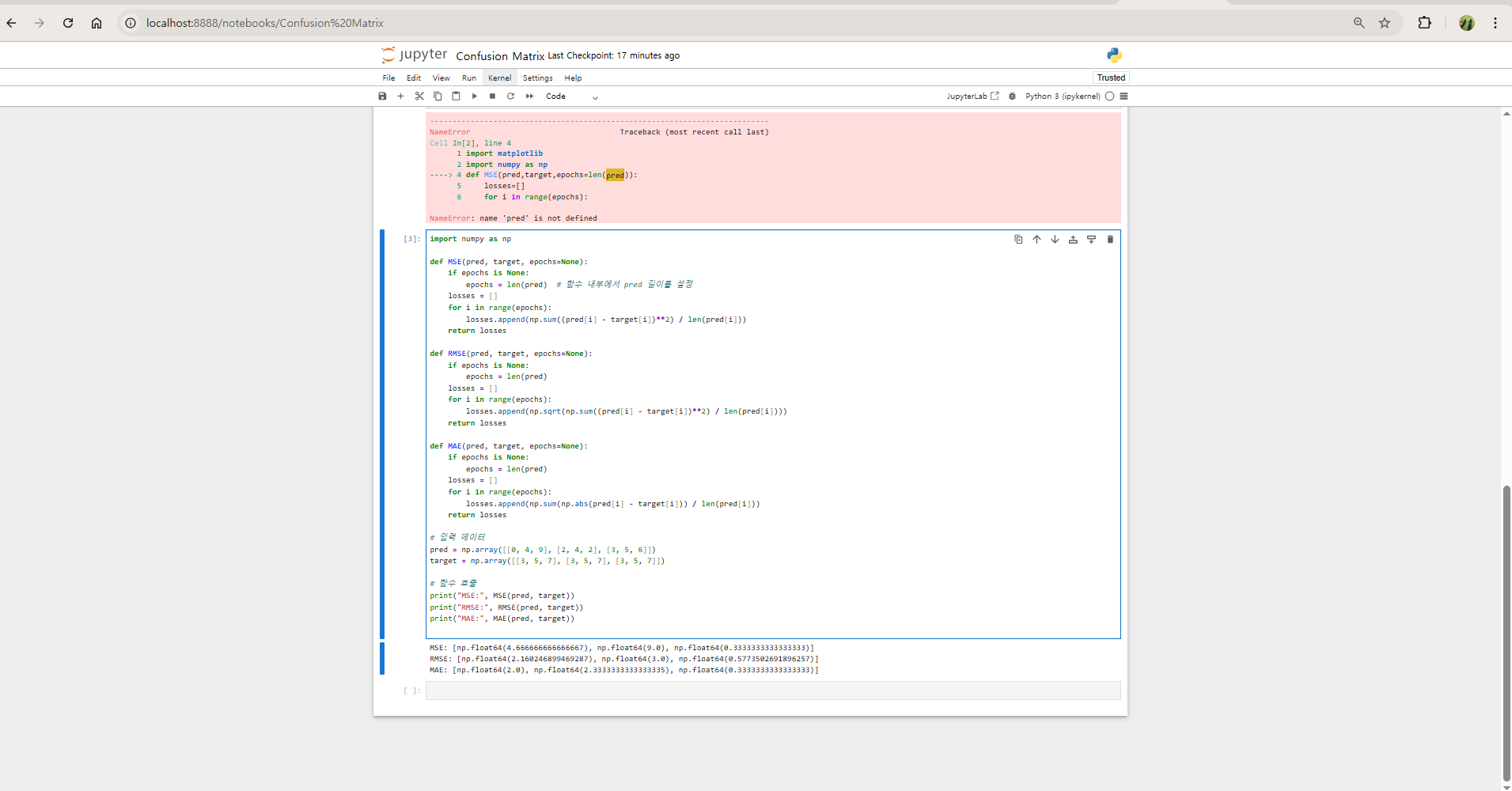

1. 평균 제곱 오차 (MSE, Mean Squared Error)

• MSE는 예측값과 실제값 간의 차이를 제곱하여 평균을 낸 값으로, 모델의 예측 성능을 측정하는 대표적인 지표입니다.

공식

$MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$

• $y_i$: 실제 값

• $\hat{y}_i$: 예측 값

• $n$: 데이터의 개수

특징

1. 큰 오차에 민감

   • 모든 오차를 제곱하여 평균을 내므로, 이상치(large outliers)가 결과에 큰 영향을 미침.

   • 작은 오차보다 큰 오차를 더 강조하고, 모델이 큰 오차를 줄이도록 유도.

2. 단위의 왜곡

   • 오차를 제곱하므로 MSE 값의 단위는 원래 데이터 단위의 제곱(예: "cm" → "cm²")이 됩니다.

   • 단위 왜곡으로 인해 해석이 직관적이지 않을 수 있음.

응용 분야

• 머신러닝 회귀 모델 성능 평가

  • 주택 가격, 온도, 판매량 등 연속형 데이터를 예측하는 모델 평가에 자주 사용됨.

• 최적화 알고리즘

  • 경사 하강법(Gradient Descent)에서 손실 함수(Loss Function)로 활용되어 모델 학습 시 MSE 값을 최소화하게 함.

예제

• 실제 값 $y = [3, 7, 5]$, 예측 값 $\hat{y} = [2.5, 8.2, 4.9]$이 있을 때

  $y$ (실제 값)	$\hat{y}$ (예측 값)	$y - \hat{y}$ (오차)	$(y - \hat{y})^2$ (제곱 오차)
  3	2.5	0.5	0.25
  7	8.2	-1.2	1.44
  5	4.9	0.1	0.01

• $MSE = \frac{1}{3} \times (0.25 + 1.44 + 0.01) = \frac{1.7}{3} \approx 0.566$
  • 따라서 MSE = 0.566.

2. 평균 제곱근 오차 (RMSE, Root Mean Squared Error)

• RMSE는 MSE의 제곱근을 취한 값으로, 결과의 단위를 원래 데이터 단위와 같게 만들어 해석을 더 직관적으로 할 수 있도록 설계된 지표입니다.

공식

$RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}$

특징

1. 큰 오차에 민감

   • MSE와 동일하게, 큰 오차의 영향을 많이 받음(오차를 제곱하므로).

   • 따라서 오차가 큰 데이터나 이상치를 더 중요하게 다룸.

2. 단위 일관성

   • 제곱근을 씌우기 때문에 RMSE의 결과는 원래 데이터와 같은 단위로 표현됩니다.

   • 예: 데이터가 "°C"라면, RMSE 결과 또한 "°C".

응용 분야

• 정밀도가 중요한 분야

  • 금융(주가 예측), 의료(질병 예측), 에너지(소비량 예측) 등 오차를 세밀하게 파악해야 하는 경우 사용.

• 손실 함수

  • 회귀 문제에서 모델 최적화를 위해 사용. 특히 수치적인 목표 예측 모델의 성능 평가에 도움을 줌.

예제

• 위의 MSE 사례에서 계산된 $MSE = 0.566$이라면

• $RMSE = \sqrt{MSE} = \sqrt{0.566} \approx 0.752$

  • 따라서 RMSE = 0.752.

3. 평균 절대 오차 (MAE, Mean Absolute Error)

• MAE는 각 데이터의 예측값과 실제값 간의 절대적인 차이(오차)를 평균낸 값으로, 결과를 직관적으로 이해하기 쉬운 지표입니다.

공식

$MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|$

특징

1. 이상치에 덜 민감

   • MSE와 달리 오차를 제곱하지 않으므로, 큰 오차가 평균에 미치는 영향이 더 적음.

2. 단순하고 직관적

   • 계산이 간단하고 결과 해석이 쉬움.

   • 실제 값과 예측 값의 평균적인 절대 오차 크기를 그대로 보여줌.

응용 분야

• 이상치 많은 데이터

  • 이상치가 많은 데이터에서 안정적인 평가가 필요할 때 적합.

  • 예: 소셜 미디어 사용량 데이터 분석, 오류가 많은 IoT 센서 데이터.

• 모델 비교

  • 여러 모델을 비교할 때 RMSE보다 이상치의 영향을 덜 받는 성능 평가 지표로 사용.

예제

• 실제 값 $y = [3, 7, 5]$, 예측 값 $\hat{y} = [2.5, 8.2, 4.9]$

  $y$ (실제 값)	$\hat{y}$ (예측 값)	$
  3	2.5	0.5
  7	8.2	1.2
  5	4.9	0.1

• $MAE = \frac{1}{3} (0.5 + 1.2 + 0.1) = \frac{1.8}{3} \approx 0.6$

  • 따라서 MAE = 0.6.

RMSE vs MSE vs MAE 비교

특징	MSE	RMSE	MAE
오차 민감도	큰 오차에 매우 민감	큰 오차에 민감	큰 오차에 덜 민감
단위의 직관성	데이터 단위의 제곱	원래 데이터 단위	원래 데이터 단위
계산 복잡성	계산이 비교적 간단	MSE에 제곱근 추가	계산 과정이 가장 간단
활용 분야	큰 오차를 중점적으로 다룰 때 필요	결과의 직관성이 필요한 경우 활용	이상치 영향을 줄이고 안정적인 평가가 필요할 때 사용

결론

• MSE: 큰 오차를 강조하고 오차를 최소화하는 데 적합.

• RMSE: 결과의 단위 일관성을 유지하면서 큰 오차를 강조. 정밀성과 직관성을 모두 요구하는 경우 사용.

• MAE: 이상치에 덜 민감하며, 안정성과 단순성이 필요한 경우 적합.

Tip: 한 가지 지표만 보지 말고, MSE, RMSE, MAE를 모두 사용하여 모델의 성능을 다각도로 평가하세요!