최소제곱법(Ordinary Least Squares, OLS): 최소제곱법(OLS)과 평균제곱오차(MSE)의 관계

calico·2025년 12월 11일

Artificial Intelligence

목록 보기

139/161

1. 최소제곱법(OLS)과 평균제곱오차(MSE)의 관계

최소제곱법(Ordinary Least Squares, OLS)은 선형 회귀 모델의 파라미터를 추정하기 위해 사용되는 대표적인 최적화 기법이다.
- OLS의 목적은 데이터의 오차 제곱합(SSE) 또는 평균제곱오차(MSE)를 최소화하는 파라미터 조합을 찾는 것이다.
한편 MSE(Mean Squared Error)는 모델이 데이터를 얼마나 잘 설명하는지를 나타내는 평가 지표이다.
- MSE는 학습 과정에서는 목표 함수(손실 함수) 로 사용되고, 학습된 모델을 평가할 때는 성능 지표(metric) 로 사용된다.

2. OLS(Ordinary Least Squares)의 개념

2.1 선형 회귀 모델

선형 회귀는 다음과 같은 모델을 가정한다.

y_i = \beta_0 + \beta_1 x_i + \varepsilon_i

여기서

$\beta_0$ : 절편
$\beta_1$ : 기울기
$\varepsilon_i$ : 오차(잔차)

모델의 예측값은 다음과 같다.

\hat{y}_i = \beta_0 + \beta_1 x_i

2.2 잔차 제곱합(SSE)

각 데이터의 오차는 다음과 같다.

e_i = y_i - \hat{y}_i

OLS는 다음의 잔차 제곱합(SSE)을 최소화한다.

SSE(\beta_0, \beta_1) = \sum_{i=1}^n (y_i - (\beta_0 + \beta_1 x_i))^2

따라서 OLS의 최적화 문제는 다음과 같다.

\min_{\beta_0,\beta_1} \sum_{i=1}^n (y_i - (\beta_0 + \beta_1 x_i))^2

3. MSE(Mean Squared Error)의 역할

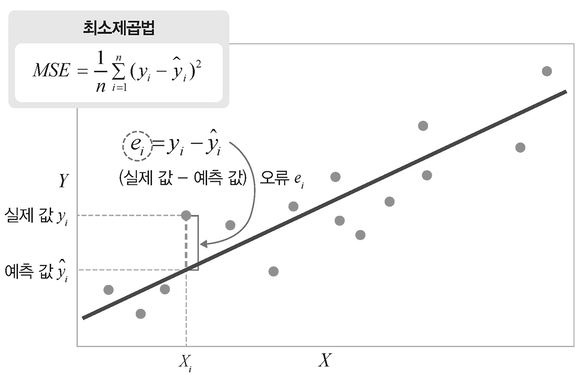
목적 함수로서의 MSE

MSE는 다음과 같이 정의된다.

MSE(\beta_0, \beta_1)=\frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2

또한 SSE와의 관계는 다음과 같다.

MSE = \frac{1}{n} SSE

따라서 SSE 또는 MSE 둘 중 무엇을 최소화하더라도 최적 파라미터는 동일하다.

학습 중에는 OLS 최적화가 곧 MSE 최소화 문제와 동일하기 때문에, MSE는 목적 함수 또는 손실 함수로 사용된다.

평가 지표로서의 MSE

최적화가 완료되면, MSE는 새로운 데이터(검증/테스트)의 모델 성능을 평가하는 지표로 사용된다.

즉 MSE는

학습 중: 최소화해야 하는 목적 함수
학습 후: 모델이 데이터를 얼마나 잘 맞추는지 측정하는 평가 지표

라는 두 가지 역할을 수행한다.

4. 예제: OLS 추정 및 MSE 계산

데이터

다음과 같은 데이터가 주어졌다고 하자.

i	$x_i$	$y_i$
1	1	1
2	2	2
3	3	2
4	4	4

OLS를 통한 파라미터 추정

평균은 다음과 같다.

\bar{x} = 2.5, \qquad \bar{y} = 2.25

기울기와 절편은 다음을 통해 구할 수 있다.

\hat{\beta}_1 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2}, \qquad \hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x}

계산 결과,

\hat{\beta}_1 = 0.9, \qquad \hat{\beta}_0 = 0

따라서 회귀식은 다음과 같다.

\hat{y} = 0.9x

학습 과정의 SSE 및 MSE 계산

데이터별 예측값 및 잔차는 다음과 같다.

i	$y_i$	$\hat{y}_i$	$e_i$	$e_i^2$
1	1	0.9	0.1	0.01
2	2	1.8	0.2	0.04
3	2	2.7	-0.7	0.49
4	4	3.6	0.4	0.16

SSE는 다음과 같다.

SSE = 0.01 + 0.04 + 0.49 + 0.16 = 0.70

MSE는 다음과 같다.

MSE = \frac{0.70}{4} = 0.175

이는 학습 시 최소화하려 했던 목적 함수의 값이다.

평가용 MSE 계산 예

테스트 데이터가 다음과 같다고 하자.

i	$x_i^{(test)}$	$y_i^{(test)}$
1	1.5	1.5
2	3.5	3.0

예측값은 다음과 같다.

\hat{y}^{(test)}_1 = 0.9 \times 1.5 = 1.35, \qquad \hat{y}^{(test)}_2 = 0.9 \times 3.5 = 3.15

오차 제곱은 다음과 같다.

0.15^2 = 0.0225, \qquad (-0.15)^2 = 0.0225

따라서 MSE는 다음과 같다.

MSE_{test} = \frac{0.0225 + 0.0225}{2} = 0.0225

이는 모델의 예측 성능을 나타내는 평가 지표로 사용된다.

5. 결론

OLS는 SSE 또는 MSE를 최소화하는 파라미터를 찾는 최적화 방법이다.
MSE는 학습 단계에서는 목표 함수(손실 함수) 로 사용되며, 학습 이후에는 모델의 성능을 평가하는 지표(metric) 로 사용된다.
동일한 MSE가 학습과 평가에서 각각 다른 역할을 수행한다는 점이 핵심이다.