[ML] Gaussian Mixture Model

바서기·2024년 3월 11일

ML

목록 보기

3/5

본 포스트는 서울대학교 데이터사이언스를 위한 머신러닝 및 딥러닝 2 이상학 교수님 수업과 수업 자료를 기반으로 작성하였습니다.
MLDL2 2번째 강의에서는 오늘 포스트의 주제인 Gaussian Mixture Model에 대해 배웠다. 저번 Bayesian Network보다 내용이 어려워 중간에 뛰쳐나갈까 싶었지만 차마 13학점 들으면서 학교 다닐 순 없어서 끝까지 버티긴 했다. 추가로 Hidden Markorv Model(HMM)에 대해서도 배웠지만 아직 Learning 파트가 남아서 다음주에 포스트를 올릴 것 같다. 오늘은 GMM까지

0. Intro.

Gaussian Mixture Model, 줄여서 GMM은 실제 생활의 확률 분포가 Gaussian distribution의 합성으로 이루어져있다고 가정한다. 따라서 몇 개의 Gaussian distribution으로 이루어져있는지 안다면 혹은 추정한다면 이를 기반으로 파라미터를 업데이트 해 데이터를 clustering한다.(혹은 clustering을 기반으로 k를 역으로 추적가능하다.)
먼저, multivariate Gaussin distribution models에서 vector $\mathbf{x}$ 의 PDF는 다음과 같다.

p(\mathbf{x}; \mu, \Sigma) = \frac{1}{(2\pi)^{\frac{d}{2}}\vert\Sigma\vert^\frac{1}{2}}exp(-\frac{1}{2}((\mathbf{x}-\mu)^T\Sigma^{-1}(\mathbf{x}-\mu)) \\\space \\ \mathbf{x}=\{x_1, x_2, ..., x_m\} \\\space \\ \mu= \frac{1}{m}\sum_{i=1}^{m}x_i \\\space \\ \Sigma= \frac{1}{m}\sum_{i=1}^{m}(x_i-\mu)(x_i-\mu)^T

여기서 $\Sigma$ 는 covariance matrix를 의미한다.
또한 확률에서 존재하는 |와 ;의 차이는 둘 다 given의 의미이지만 ;뒤의 변수들을 함수를 생성하는 parameter의 의미가 있다.

1. Gaussian Mixture Model(GMM)

1.1 GMM Intro

GMM이 나타내는 $\mathbf{x}$ 의 확률 분포는 다음과 같다.

p(\mathbf{x})=\sum_{k=1}^K\pi_k\cdot\mathcal{N}(\mathbf{x};\mu_k,\Sigma_k)

여기서 $\pi_k$ 는 mixing coefficients로

\sum_{k=1}^K\pi_k=1, and\space \pi_k\ge0

를 만족한다.
GMM을 density estimator이라 하는데 이는 주어진 데이터의 확률 밀도 함수(PDF)를 추정하기 때문이다. 그래서 다른 말로 universal approximators of densities라고도 한다.

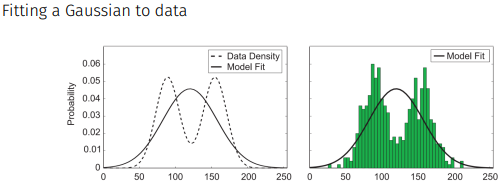
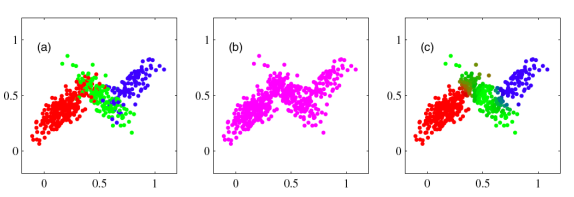
이렇게 data의 분포가 생겼을 때 하나의 gaussian으로는 전체를 잘 표현하지 못하지만

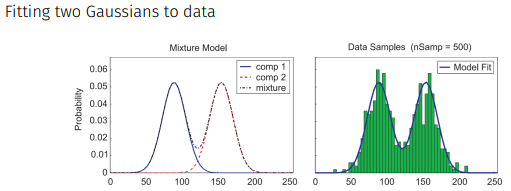
두 개의 gaussian으로는 야무지게 표현한다.

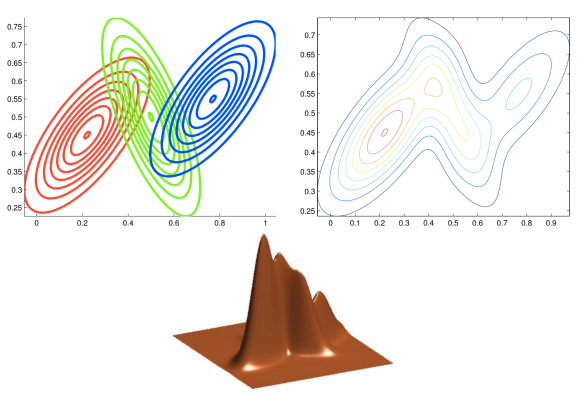
이는 2D에서도 마찬가지

1.2 Fitting GMMs: Maximum Likelihood

Maximum likelihood, 최대 우도는 통계학에서 매개변수적 모델의 매개변수 값을 추정할 때 주어진 데이터가 관찰될 확률을 최대화하는 매개변수의 값을 찾는 것으로 GMM에 maximum likelihood를 적용하는 것은 mixing coefficients과 gaussian distributions의 평균과 공분산을 찾는 것이다.
즉, Maximum likelihood는

\ln P(\mathbf{X};\pi, \mu, \Sigma)=\sum_{i=1}^N\ln(\sum_{k=1}^K\pi_k\mathcal{N}(\mathbf{x}^{(i)};\mu_k,\Sigma_k)) \\ w.r.t \space \Theta=\{\pi_k,\mu_k, \Sigma_k\}

를 최대화하는 것이다.(작을 수 있어 ln씌움.)
+ 여기서 헷갈릴 수 있는 부분이 GMM의 목표는 X가 나타날 '확률'을 최대화하는 것이 아니라 '확률 밀도(그 값 근처에서 관찰될 데이터의 밀도
)'를 최대화 하는 것, 따라서 확률 밀도 함수의 값을 가중합해준 것을 최대화한다.
하지만 여기서 2가지 문제점이 발생하는데
1. Singularities(특이성): gaussian 분포가 하나의 point를 설명하면 공분산이 매우 작아져 likelihood가 무한히 커질 수 있는 현상(노이즈에 과하게 적응하게 만들기 때문에 문제)
2. Identifiability(식별성): GMM의 파라미터에 대한 추정이 순열에 대해 달라질 수 있음 = 특정 데이터 세트를 설명할 수 있는 여러 개의 파라미터 세트가 존재함
들이다. 따라서 각각을 공분산의 최소 크기에 제약을 두는 것 + 모델 선택 기준을 사용하여 적절한 클러스터 수를 결정하는 것과 특정 클러스터에 대한 해석이나 라벨링을 수행할 때 이러한 속성을 이해하는 것으로 해결하거나 완화해야 한다.(kmeans랑 유사하다...)

1.3 Trick: Introduce a Latent Variable

우리는 GMM을 simplify하기 위해 hidden varible인 $Z$ 를 도입할 것인데 $Z$ 는 위에서 소개한 missing coefficients를 확률로 가지면서 관측값 $x$ 가 어떤 가우시안에서 생성되었는지를 나타낸다.
즉, $Z\sim Categorical(\pi)$ (where $\pi_k\ge0, \sum_k\pi_k=1$ )이고

p(\mathbf{x})=\sum_{k=1}^Kp(\mathbf{x}, Z=k) \\ =\sum_{k=1}^Kp(z=k)p(\mathbf{x}\mid Z=k)

가 성립한다.(최종식의 앞부분이 $\pi_k$ 를 의미하고 뒷부분이 $\mathcal{N}(\mathbf{x}|\mu_k,\Sigma_k)$ 를 의미한다.)
이를 그래프의 관점에서 2가지로 볼 수 있다.

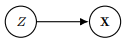
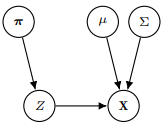
이렇게 항상 unobserved되는 variables를 latent variables or hidden variables라 한다.
GMM에서 각 data point가 어떤 gaussian distribution에서 생성되었는지는 직접적으로 관찰할 수 없는 latent variables이다. 따라서 이 잠재변수의 값을 추론하는 것이 GMM의 목표 중 하나가 된다.(EM 알고리즘으로 각 구성 요소에 속할 확률을 추정함으로써)
정리해보면 GMM에서 a Gaussian mixture distribution은

p(\mathbf{x})=\sum_{k=1}^K\pi_k\cdot\mathcal{N}(\mathbf{x};\mu_k,\Sigma_k)

인데 우리는 $Z\sim Categorical(\pi)$ 와 joint distribution $p(\mathbf{x},z)=p(z)p(\mathbf{x}\mid z)$ 을 통해 log-likelihood인

\mathcal{l}(\mathbf{\pi},\mu,\Sigma) =\sum_{i=1}^{N}\ln p({x}^{(i)};\pi, \mu, \Sigma) \\ =\sum_{i=1}^{N}\ln p(x^{(i)}\mid z^{(i)};\mu, \Sigma)p(z^{(i)};\mathbf{\pi})

를 유도했고 모든 data point에 대해 $z^{(i)}$ 라는 hidden varibales를 도입했다.
이제 위 확률을 optimize해야 하는데 문제점이 sum안에 있는 log이다. 이를 어떻게 해결하는지 1.4부터 알아보자.

1.4 Optimize Maximum Likelihood

만약에 우리가 $z^{(i)}$ 를 알고 있다면(= $Z$ 의 분포인 $I$ 를 안다면) maximum likelihood problem은 간단하게 풀린다.

\mathcal{l'}(\mathbf{\pi},\mu,\Sigma) =\sum_{i=1}^{N}\ln p(x^{(i)}, z^{(i)};\pi, \mu, \Sigma) \\ =\sum_{i=1}^{N}(\ln p(x^{(i)}\mid z^{(i)};\mu, \Sigma)+\ln p(z^{(i)};\mathbf{\pi}))

식은 생략하면

\mu_k = \frac{\sum_{i=1}^NI(z^{(i)}=k)\mathbf{x}^{(i)}}{\sum_{i=1}^NI(z^{(i)}=k)} \\\space \\ \Sigma_k= \frac{\sum_{i=1}^NI(z^{(i)}=k)(\mathbf{x}^{(i)}-\mu_k)(\mathbf{x}^{(i)}-\mu_k)^T}{\sum_{i=1}^NI(z^{(i)}=k)} \\\space \\ \pi_k = \frac{1}{N}\sum_{i=1}^NI(z^{(i)}=k)

이 나온다.(사실 직관적으로도 설명해볼라 했는데 설명이 안된다.ㅜㅜ 나중에 보완해볼게요..)
하지만 우리는 Z의 분포를 모르기 때문에 Expectation Maximization이라는 algorithm을 통해 optimize할 것이다.

2. Expectation Maximization

2.1 Intro

이 Expectation Maximization algorithm(줄여서 EM)은 2가지 steps을 거친다.
1. E-step: 각 Gaussian이 data point에 대해 만들어 내는 posterior probability를 계산한다.(현재 매개변수 추정치를 기반으로 각 데이터 포인트가 특정 클러스터에 속할 조건부 확률을 계산)(k가 clusters중 하나를 의미)

\gamma_k^{(i)}=P(z^{(i)}=k\mid \mathbf{x}^{(i)}, \pi, \mu, \Sigma)

M-step: log likelihood를 최대화 하도록 Gaussian의 parameters를 update한다.(데이터는 E-step에서 계산한 분포에서 생성되었다고 가정, 새로운 분포 추가 x)
$\frac{\partial\ln p(\mathbf X; \pi, \mu, \Sigma)}{\partial \Theta} \\\space \\ w.r.t \space \Theta=\{\pi_k,\mu_k, \Sigma_k\}$

위 과정을 log likelihood가 의미있게 변하지 않을 때까지 반복한다.

2.2 E-step: Responsibilities

각 데이터 포인트가 모델 내의 각 가우시안 분포에 속할 확률을 나타내므로 각 가우시안 분포가 데이터 포인트를 얼마만큼 '소유'하는지로도 해석할 수 있어 responsibilities의 관점으로 볼 수 있다.

2.3 M-step: Estimate Parameters

먼저 $\Theta$ 의 멤버 중 하나인 $\mu_k$ 에 대해 미분해보면

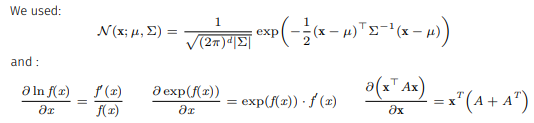
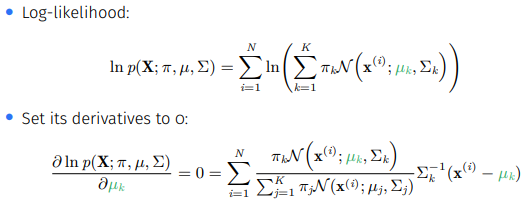
+ 위 식처럼 어떤 문제의 해를 명시적인 수식으로 표현할 수 없을 때 closed-form이 존재하지 않는다고 한다. 따라서, 앞쪽의 $\mu_k$ 를 fix시켜 해를 구한다.(초록색이 사라짐.)

가 되는데 $N_k$ 는 cluster k에 실질적으로 들어있는 data points의 수를 의미한다.
즉, GMM은 클러스터의 중심을 update할 때 Gaussian이 책임지는 데이터의 무게 중심을 구하는데 이는 k-means에서와 같지만 가우시안의 사후 확률(posterior probability)에 의해 가중된다는 점이 다르다.
마찬가지로 $\Sigma_k$ 와 $\pi_k$ 에 대해서도 미분을 진행하면

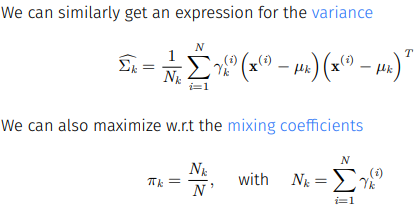
이고 optimal mixing proportion은 해당하는 Gaussian이 책임지는 data의 비율을 의미한다.
즉, EM algorithm은

이렇게 E-step에서 계산한 posterior probabilities를 가지고 각 cluster의 중심, 분산, 비율을 update하며 likelihood를 개선한다.

2.4 Mixture of Gaussians vs K-means

EM for mixtures of Gaussians는 k-means의 soft version같다.
Hard assignments(데이터 포인트와 클러스터간의 거리(보통 유클리드 거리)->k-means)를 E-step에서 할당하지 않고 squared Mahalanobis distance를 기반하는 soft assignments(하나의 클러스터에만 전적으로 할당하는 것이 아니라, 모든 클러스터에 대한 소속 확률을 계산하여 할당)를 했기 때문이다.
+ Mahalanobis distance
데이터 포인트와 평균 사이의 거리를 측정할 때 데이터의 분산을 고려해 스케일이 다른 특성 간의 비교를 표준화하고, 특성 간의 상관 관계를 반영하여 더 의미있는 거리 측정값을 제공함.

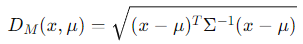
또한 각 클러스터의 중심이 soft assignments에게 제공받은 data의 가중 평균을 기반으로 움직이는 반면 k-means는 weights가 0 or 1이다.

2.5 1,2장 Summary - GMM

우선 모델에서
- GMM은 clustering에 probabilistic view를 도입하여 각각의 cluster를 다른 Gaussian에 대입하여 생각한다.
- Latent variables을 도입하여 복잡한 혼합 구조를 효과적으로 모델링하고, 각 데이터 포인트의 클러스터 소속에 대한 불확실성을 유연하게 만들었다.+결측치와 불완전한 데이터 처리에도 유리하다.
- GMM은 Gaussian 분포에 국한하지 않고 continuous, disrete등의 다른 분포로 대체 가능한 유연한 model이다.
다음은 알고리즘에서
- Optimization은 EM algorithm을 기반으로 작동한다.
- 각 반복에서 lower bound를 계산하고 최적화한다.
- step-size가 필요하지 않다.
- local maxima나 local minima에 수렴할 수 있다.(k-means로 출발하는 아이디어 있음. 이유는 log likelihood function이 non-convexity하기 때문.)
- 한계: $P(\mathbf{z\mid x};\Theta)$ 를 계산할 수 있어야 한다. 복잡한 모델에서 계산이 어려우면 Variational Inference를 사용한다.
+ Variational Inference
사후 분포를 근사하는 더 단순한 분포를 선택하고 근사 분포를 최적화 해 실제 사후 분포에 가깝도록 만든다. 척도로는 KL Divergence(Kullback-Leibler Divergence)를 사용하고 최적화 방법으론 경사 하강법을 일반적으로 사용한다.

3. A bit more on EM

이번 장에선 2.5에서 algorithm에 대한 summary의 내용들을 확인해보고 근본적으로 EM algorithm이 왜 작동하는지에 대해 수식으로 보일 것이다.(어마무시하다...)

3.1 Where does EM come from?

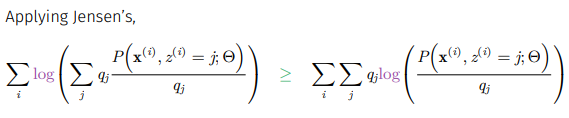
하한에 대한 이야기를 하기 위해 억지로 식을 변형해주고 log function이 concave하다는 성질을 통해 Jensen's inequality를 사용해줄 것이다.

3.2 EM derivation

만약 $q_i$ 를 아래와 같이 잡아주면

위 부등식은 $\Theta$ 가 $\Theta_{old}$ 와 같을 때 성립하는 부등식이 된다. 즉,

l(\mathbf{X},\Theta) \ge \sum_i\sum_jP(z^{(i)}=j\mid\mathbf{x}^{(i)},\Theta)\log (P(\mathbf{x}^{(i)};\Theta)) \\\ge \sum_i\sum_jP(z^{(i)}=j\mid\mathbf{x}^{(i)},\Theta^{old})\log (P(\mathbf{x}^{(i)};\Theta^{old})) \\ =\sum_i\log (P(\mathbf{x}^{(i)};\Theta^{old}))=l(\mathbf{X},\Theta^{old})

이를 $q_j$ 가 고정되어있을 때

로 볼 수 있다. 의미를 해석하면 E-step에서 계산되는 likelihood는 $q_j$ 가 고정되어있으면 개선될 수 있다는 것이다. 이를 시각화 하면

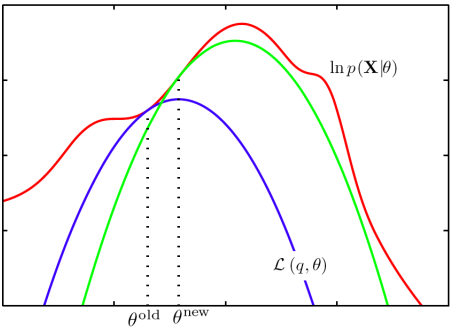
이렇게 되어 q가 고정되어 있는 파란색 likelihood에서 $\theta_{new}$ 로 개선이 되고 그 값에서 새로운 q에 대한 likelihood funtion의 하한을 찾게 된다. 즉, E-step에선 우도 함수의 하한선을 계산하고 M-step에서 그 하한선을 최대화하는 새로운 매개변수 값을 찾게 되며 이 과정을 반복한다.

그럼 왜 E-step이 expectation step이라 불리냐면 실제 EM algorithm은 위에선 정의한 $Q(\Theta)$ , 로그 우도 함수의 기댓값을 E-step에서 계산하기 때문이다. E-step에서 $\Theta_{old}$ 와 사후 확률(z의 분포를 모르기 때문)로 $Q(\Theta)$ 를 계산하고 M-step에서 $Q(\Theta)$ 를 최대화 하는 새로운 $\Theta$ 를 찾아 로그 우도 함수의 하한을 개선한다. 이 때, $Q(\Theta_{old})$ 는 실제 로그 우도의 $\Theta_{old}$ 를 대입했을 때와 같고 $Q(\Theta)$ 를 최대화하면서 log likelihood를 최대화 하기 때문에 간접적으로 최대화한다고 한다.

3.3 3장 Summary

GMM은 관측되지 않은 잠재 변수를 포함하여 로그 우도 함수를 직접 최대화하는 것이 어렵다. 따라서 간접적인 방법으로 최대화하기 위해 로그 우도 함수의 기댓값인 $Q(\Theta)$ 를 정의하고 이를 로그 우도 함수의 하한값으로 생각해 하한값을 개선하는 방향으로 로그 우도 함수를 최대화 한다. EM 알고리즘은 E-step과 M-step으로 이루어져 있어 하한값을 계산하는 단계, 하한값을 개선하는 단계로 나뉜다.

4. 느낀점

이 모든 내용을 1시간만에 나갔을 때 진심으로 머리가 지끈했다(어이없어서 웃음이 나옴). 그래도 이제는 어느정도 이해가 된거 같아 오늘 배운 내용을 정리하면 Gaussian mixture model의 구성부터 k-means에 비해 어떤 장점을 갖는지 그리고 parameters를 개선하는 EM algorithm이 왜 작동하는지까지 배웠다. 다행이 다음번 진도를 나간 hidden markorb model은 좀 이해가 되었는데 솔직히 앞으로 갈길이 막막하다. 하하. 하지만 이제 빼기엔 늦었기에 최선을 다해 노력해보겠다. 나에게는 gpt가 있거든!

바서기

인생 법칙 1. 기준 낮추기 않기 2. 일단 해보기 3. 긍정 마인드