✍🏻 20일, 21일 공부 이야기.
👀 오늘 공부한 내용의 실습 코드는 아래 깃허브에 올려두었습니다.
https://github.com/castlemi99/ZeroBaseDataSchool/tree/main/Machine%20Learning
Pipeline(파이프라인)
from sklearn.pipeline import Pipeline
데이터 전처리와 여러 알고리즘들을 반복 실행하고 더 나아가 파이퍼파라미터 튜닝 과정을 번갈아하다보면 코드의 실행 순서에 혼돈이 있을 수 있다.
이 혼돈을 막기 위해 sklearn유저가 사용할 수 있는 기능이 바로 Pipeline이다.
앞서 실습했던 와인 데이터를 이용해 자세히 알아보자.
# 데이터 읽기
import pandas as pd
red_url = 'https://raw.githubusercontent.com/PinkWink/ML_tutorial/master/dataset/winequality-red.csv'
white_url = 'https://raw.githubusercontent.com/PinkWink/ML_tutorial/master/dataset/winequality-white.csv'
red_wine = pd.read_csv(red_url, sep = ';')
white_wine = pd.read_csv(white_url, sep = ';')
# 와인 색상 구분 컬럼
red_wine['color'] = 1
white_wine['color'] = 0
# 두 데이터 합치기
wine = pd.concat([red_wine, white_wine])
X = wine.drop(['color'], axis=1)
y = wine['color'] # 타겟 데이터데이터를 먼저 읽어들이고
만약 레드/화이트 와인 분류기를 제작하는 과정을 Scaler(StandardScaler()) -> clf(DecisionTreeClassifier()) 이렇게 짜고 싶다고 생각해보자.
그렇다면 이 과정을 Pipeline을 통해 각 단계의 (객체명, 객체)를 집어넣어주면 된다.
아래 코드에서 사용된 변수명 estimators, scaler, clf, pipe는 원하는 변수명으로 사용하면 된다.
from sklearn.pipeline import Pipeline
# 원하는 작업 import
from sklearn.tree import DecisionTreeClassifier
from sklearn.preprocessing import StandardScaler
estimators = [
('scaler', StandardScaler()), # 첫번째 단계의 (객체 이름, 객체)
('clf', DecisionTreeClassifier()) # 두번째 단계의 (객체 이름, 객체)
]
pipe = Pipeline(estimators) # 파이프라인 생성이렇게 만들어진 pipe 변수 안에는
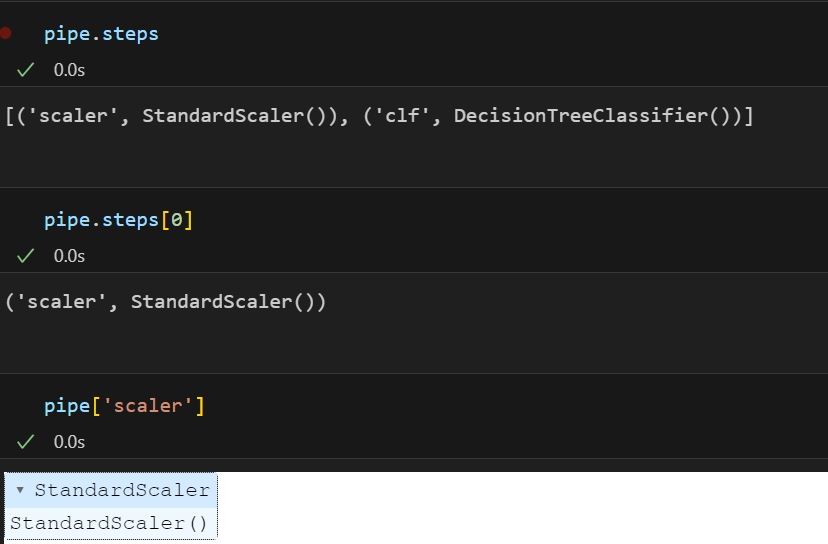
원하는 값을 호출할 수도 있다.
지금은 분류기만 만들어둔 상태이고(예를 들어 붕어빵 틀만 구입해둔 상태!) 그 안의 파라미터들을 지정해주어야한다.(붕어빵 속을 무엇으로 할지 정하는 단계)
파라미터 지정은 pipe.set_params(객체명__파라미터명 = 값) 을 이용하면 된다. (언더바_가 2개인 것에 주의⭐)
간단하게 DecisionTree의 max_depth와 random_state 파라미터만 조정한다고 하면 아래와 같이 작성할 수 있다.
# 아직 분류기만 만들어낸거지 그 안의 파라미터들도 지정해주어야한다.
# 파라미터 지정은 아래와 같은 방법으로 할 수 있다.
# pipe.set_params(객체명__파라미터명 = 값)
pipe.set_params(clf__max_depth = 2)
pipe.set_params(clf__random_state = 13)이후 과적합 방지를 위해 훈련용/테스트용 데이터를 분리해주고 학습(fit)시킨 후 성능을 평가하면 된다.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,
test_size = 0.2,
random_state=13,
stratify= y
)
# 이전에는 스케일러를 통과시키고 분류기에 학습시켜두었는데
# 그 과정이 pipe 변수에 저장이 되어있으므로 간단하게 아래 코드로 실행 가능하다.
pipe.fit(X_train, y_train)
from sklearn.metrics import accuracy_score
y_pred_tr = pipe.predict(X_train)
y_pred_test = pipe.predict(X_test)
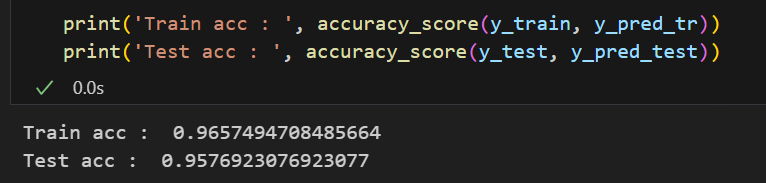
print('Train acc : ', accuracy_score(y_train, y_pred_tr))
print('Test acc : ', accuracy_score(y_test, y_pred_test))💻 출력
코드의 실행이 헷갈리지 않고 코드도 한결 간단해졌다 😊
그렇다면 이제 붕어빵 속을 어떻게 다양하게 만들 수 있는지, 어떻게 하면 맛있는 붕어빵이 만들어질 수 있을지에 대한 여러가지 방법을 배워보자.
하이퍼파라미터 튜닝
교차검증
from sklearn.model_selection import KFold
from sklearn.model_selection import StratifiedKFold
앞서 <과적합>이라는 단어를 많이 사용했었다.
과적합이란, 모델이 학습 데이터에만 과도하게 최적화된 현상으로 학습 데이터가 이 세상 모든 데이터를 대표하는 것은 아니기 때문에 좀 덜 최적화되도록 튜닝하는 것이 필요했다.
흠.. 나에게 있는 것이라곤 이 데이터 밖에 없는데 이 데이터들을 어떻게 좀 더 효과적으로 사용할 수 있을까??
그래서 우리는 훈련용과 테스트용의 데이터를 분리하는 작업을 했었다.

위와 같이 일부분을 테스트용의 데이터로 나누어서 말이다.
지금 배울 교차검증은 훈련용 데이터를 또 훈련용 / 검증용 데이터로 분리하여 검증을 좀 더 여러 번 한 작업이라고 생각할 수 있다.
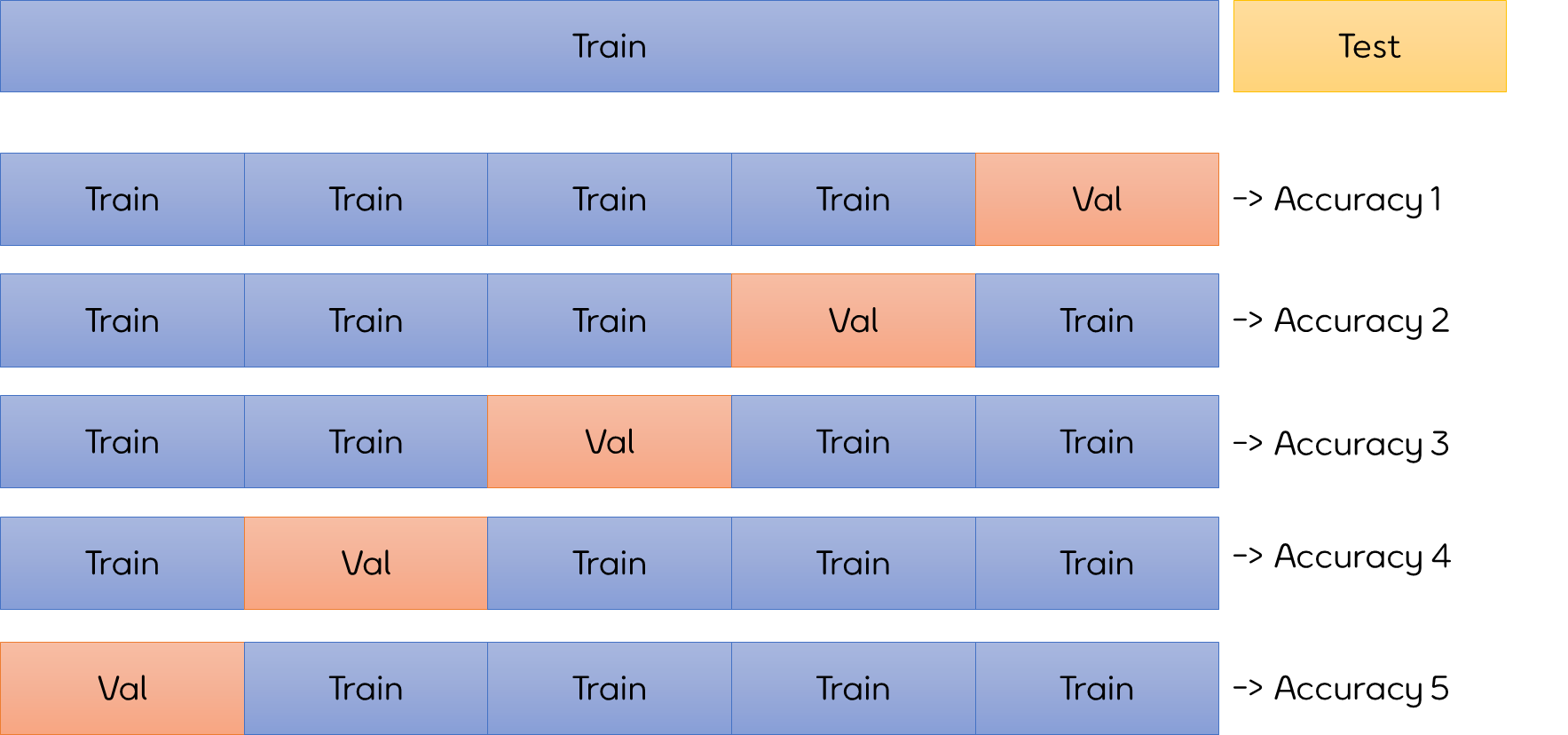
Test 셋은 냅두고 Train 셋을 Train과 Validation 데이터로 구분하는데 Validation의 범위를 각각 달리하여 5번의 정확도를 구하고 그 평균을 이 모델의 성능이라고 평가하는 것이다.
검증하는 것을 3번이든, 5번이든, 여러번 한다는 의미로 교차검증을 k-fold croos validation이라 부른다.
또한 각 구분된 데이터 셋에 타켓 데이터의 비중을 비슷하게 맞추어 분리하는 것을 stratified k-fold cross validation이라 한다.
import numpy as np
from sklearn.model_selection import KFold
X = np.array([
[1,2], [3,4], [5,6], [7,8]
])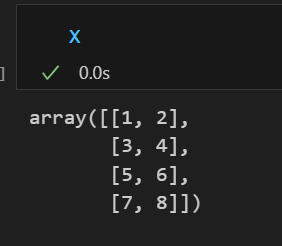
예를 들어 위와 같은 데이터 X가 있다고 하자.
데이터가 크지 않으므로 2등분(n_splits = 2)으로 데이터를 나눈다고 생각하면 아래와 같이 나눌 수 있다.
kf = KFold(n_splits=2) # 데이터를 총 2등분으로 나눔
# kfold는 인덱스를 반환하므로 데이터 값을 얻기 위해서는 아래와 같이 인덱스 지정으로 해주어야함
for train_idx, val_idx in kf.split(X):
print("==============================")
print('train data : ', X[train_idx])
print('val data : ', X[val_idx])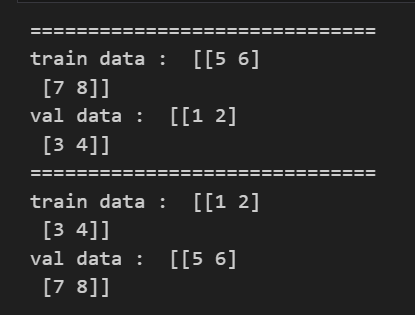
⭐ 이때 주의해야할 것은 kfold는 인덱스를 반환하므로 인덱스 지정을 통해 데이터를 구분해주어야한다!!!
그렇다면 이번에는 와인 데이터를 이용해 일단 훈련용 / 테스트용 데이터로 나누어 테스트용 데이터 성능을 여러번 체크한다고 생각하여 교차검증을 진행해보자.
똑같이 데이터를 불러들이고 이번에는 taste필드를 만들어 와인이 맛있다/맛없다를 구분하는 분류기를 만들어보려고 한다.
X = wine.drop(['color'], axis=1)
y = wine['color'] # 타겟 데이터
wine['taste'] = [1. if grade > 5 else 0. for grade in wine['quality']]
X = wine.drop(['taste', 'quality'], axis = 1)
y = wine['taste']
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
X_train, X_test, y_train, y_test = train_test_split(X,y,
test_size = 0.2,
random_state=13,
stratify= y
)
# 학습
wine_tree = DecisionTreeClassifier(max_depth=2, random_state=13)
wine_tree.fit(X_train, y_train)
# 예측
y_pred_test = wine_tree.predict(X_test)
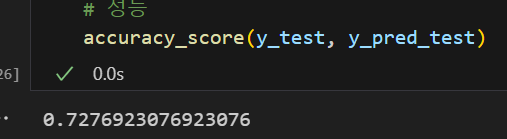
# 성능
accuracy_score(y_test, y_pred_test)💻 출력
위 코드는 우리가 이전에 했던 방법이다. 보다시피 테스트 데이터에 대해 성능이 하나만 나온다.
우리는 데이터를 5등분하여 5번의 성능을 평가해볼 것이다.
from sklearn.model_selection import KFold
kfold = KFold(n_splits=5)
wine_tree_cv = DecisionTreeClassifier(max_depth=2, random_state=13)
cv_acc = []
for train_idx, test_idx in kfold.split(X):
X_train = X.iloc[train_idx]
X_test = X.iloc[test_idx]
y_train = y.iloc[train_idx]
y_test = y.iloc[test_idx]
wine_tree_cv.fit(X_train, y_train)
pred = wine_tree_cv.predict(X_test)
cv_acc.append(accuracy_score(y_test, pred))
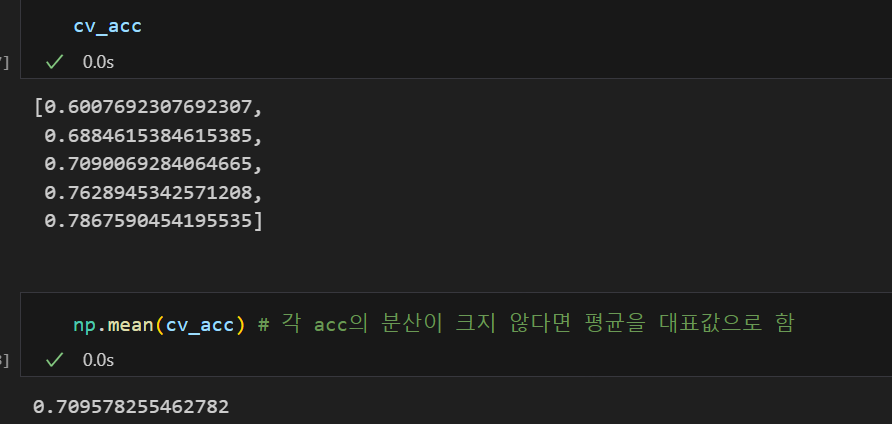
np.mean(cv_acc) # 각 acc의 분산이 크지 않다면 평균을 대표값으로 함💻 출력
n_splits = 5로 지정한 후 accuary_score를 5번 측정하면 위와 같이 cv_acc에는 5개의 정확도가 있게 되고
각 정확도의 분산이 크지 않다면 우리는 평균을 대표값으로 설정하면 된다.
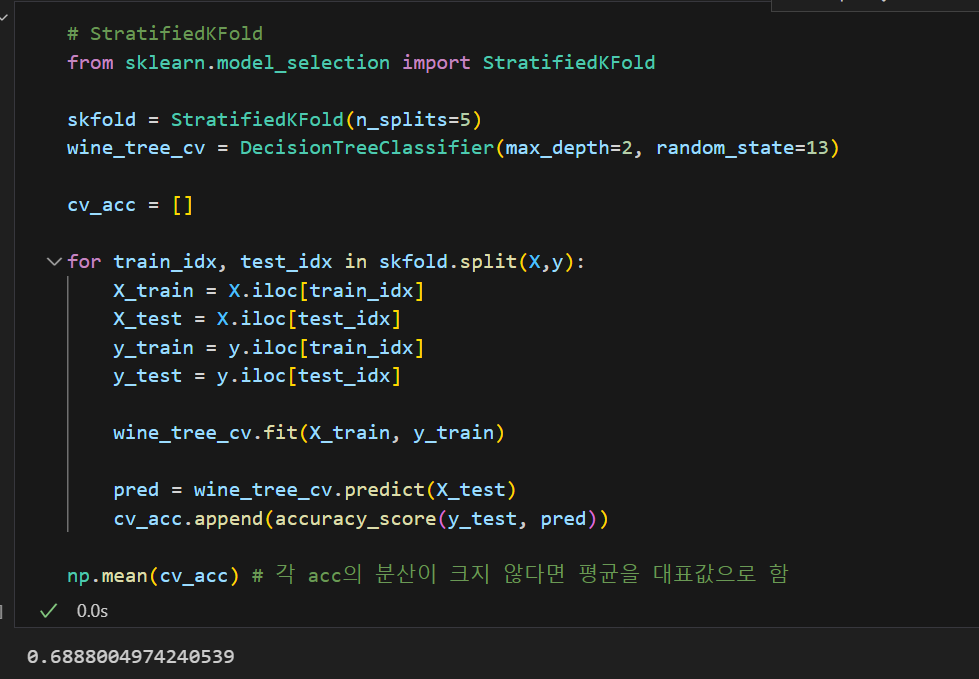
앞서 설명한 StratifiedKFold도 사용해보면 위와 같은 결과가 나오는데 성능이 점점 떨어지는 것을 볼 수 있다.
이런 경우, 내가 지금 만든 모델이 그리 좋은 성능만을 가지고 있진 않구나라고 생각하고 다른 작업을 또 해볼 수 있는 것이다.
추가로 위와 같이 인덱스로 데이터를 분리하고 성능을 구할 수도 있지만 간편하게 성능을 구할 수 있는 방법도 있다.
from sklearn.model_selection import cross_val_score
skfold = StratifiedKFold(n_splits=5)
wine_tree_cv = DecisionTreeClassifier(max_depth=2, random_state=13)
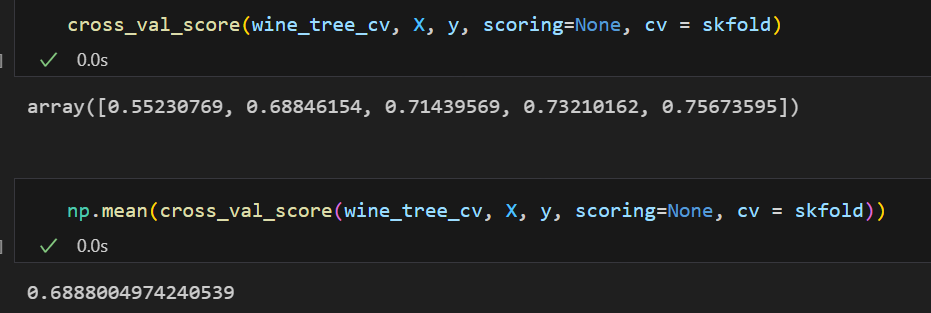
cross_val_score(wine_tree_cv, X, y, scoring=None, cv = skfold)💻 출력
바로 cross_val_score를 사용하는 것이다.
cross_val_score(분류기, X 데이터, y 데이터, cv = 교차검증변수)를 설정해주면 각각의 검증의 성능이 나오고 이를 대표값으로 다시 추출하면 된다.
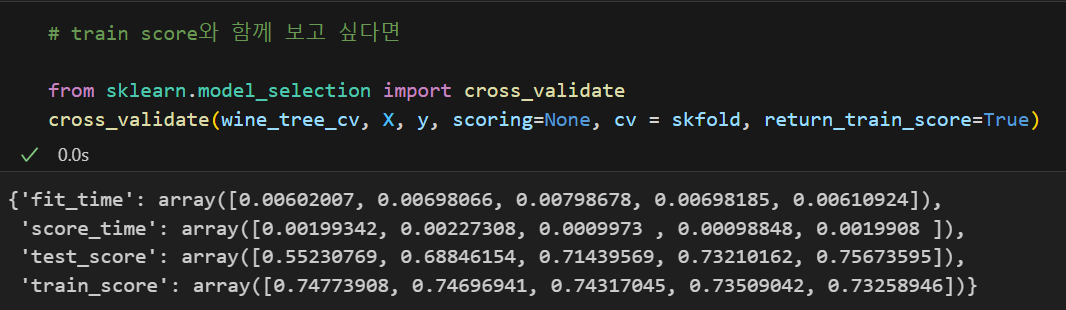
또한 Train 데이터의 성능도 같이 보고 싶다면 cross_validate를 이용하면 된다. Train 데이터의 성능까지 같이 살펴보니 지금 분류기에서는 과적합 현상이 발생해 모델의 성능이 그리 좋지는 않아 보인다는 인사이트를 발견할 수 있다.
하이퍼파라미터 튜닝
하이퍼파라미터 튜닝이란 붕어빵의 속을 무엇으로 변경해야 모두가 맛있어하는 맛이 나올까 고민하는 것과 같이 모델의 성능을 확보하기 위해 조절하는 설정값이다.
이는 일일이 다 조절해보는 수 밖에 없는데, 그나마 GridSearchCV가 우리에게 도움을 준다.
GridSearchCV
from sklearn.model_selection import GridSearchCV
우리가 조절해야하는 파라미터의 수가 엄청 많을 것이다. 파라미터가 5개라고 해도 각 파라미터에 들어갈 값들과 그 파라미터들을 조절해서 만들 수 있는 분류기의 경우의 수는 엄청 많다.
이를 좀 더 간단히 나타낼 수 있게 해주는 것이 GridSearchCV이다.
결과를 확인하고 싶은 파라미터를 정의하고 이를 GridSearchCV에 넣어주면 된다.
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeClassifier
params = {'max_depth' : [2,4,7,10]} # {'파라미터명' : 파라미터 값}
wine_tree = DecisionTreeClassifier(max_depth=2, random_state=13)
gridsearch = GridSearchCV(estimator= wine_tree, param_grid=params, cv = 5)
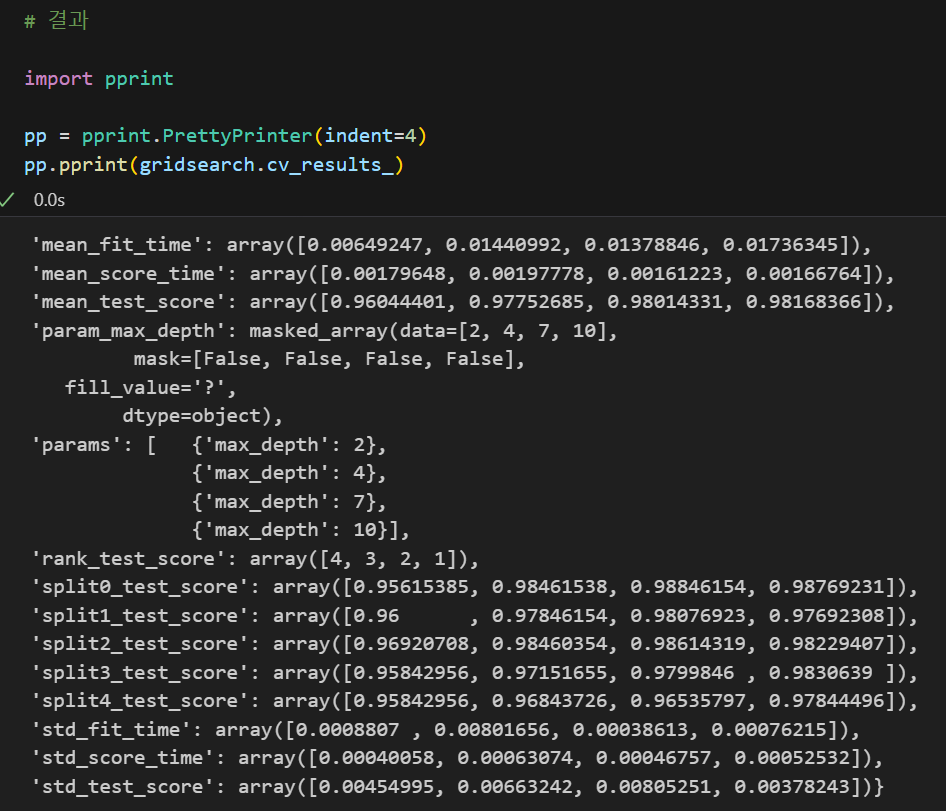
gridsearch.fit(X,y){'파라미터명' : 파라미터 값} 형태로 원하는 파라미터와 파라미터 값을 넣어준 변수를 GridSearchCV(estimator= wine_tree, param_grid=params) 에 넣어주면 되는 것이다.
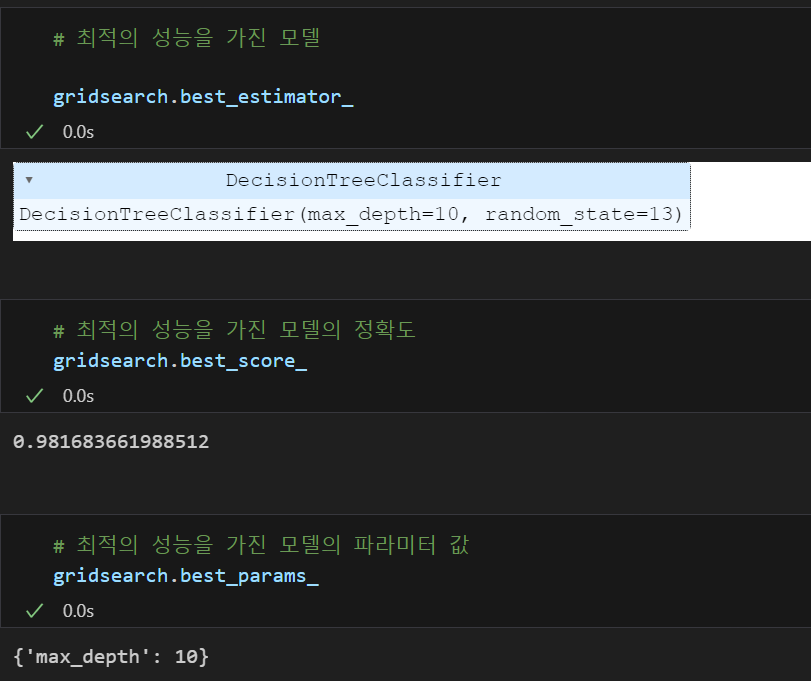
이렇게 학습시킨 모델은
 |  |
|---|
다양한 방법으로 결과를 확인할 수 있다.
📌 만약 pipeline에 GridSearch를 적용하고 싶다면???
from sklearn.pipeline import Pipeline
from sklearn.tree import DecisionTreeClassifier
from sklearn.preprocessing import StandardScaler
estimators = [
('scaler', StandardScaler()), # 첫번째 단계의 (객체 이름, 객체)
('clf', DecisionTreeClassifier()) # 두번째 단계의 (객체 이름, 객체)
]
pipe = Pipeline(estimators)
# 파라미터 조정
param_grid = [
{'clf__max_depth' : [2,4,7,10]}
]
gridsearch = GridSearchCV(estimator= pipe, param_grid=param_grid, cv = 5)
gridsearch.fit(X,y)앞서 파이프라인에서 파라미터 값을 clf__파라미터명으로 작성했던 것처럼 작성해주고 이를 GridSearchCV에 넣어주면 된다.
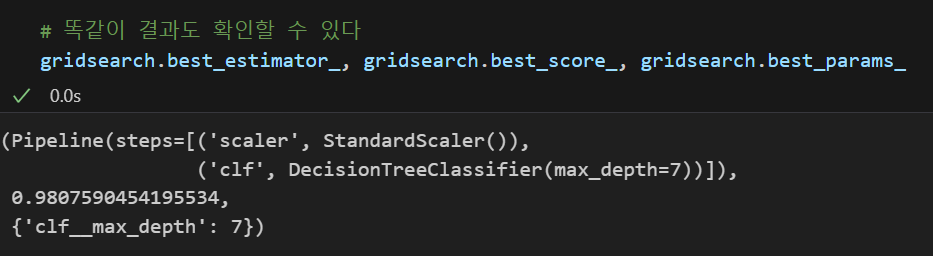
똑같이 결과도 확인할 수 있다.
만약 정확도를 좀 더 깔끔하게 데이터프레임으로 확인하고 싶다면 아래의 방법을 시도해볼 수도 있다.
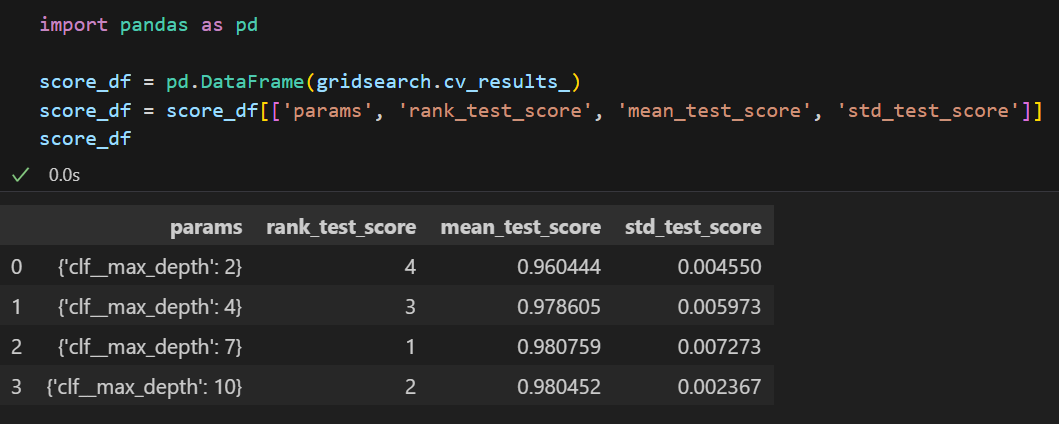
GridSearchCV를 통해 만들어진 값의 원하는 필드만 추출하여 보면 훨씬 깔끔하다 :)
모델 평가
그렇다면 어떤 모델이 좋다고 말할 수 있을까?
예를들어, 회귀모델들은 실제값과 예측값의 차이를 가지고 계산해서 그 에러가 최소가 되게 하는 모델을 선택한다.
하지만 분류 모델은 정확도(accuracy), 오차행렬(confusion matrix), 정밀도(precision), 재현율(recall), f1-score 등 평가 항목이 조금 많다.
이들에 대해 한 번 살펴보자.
이진 분류 모델의 평가
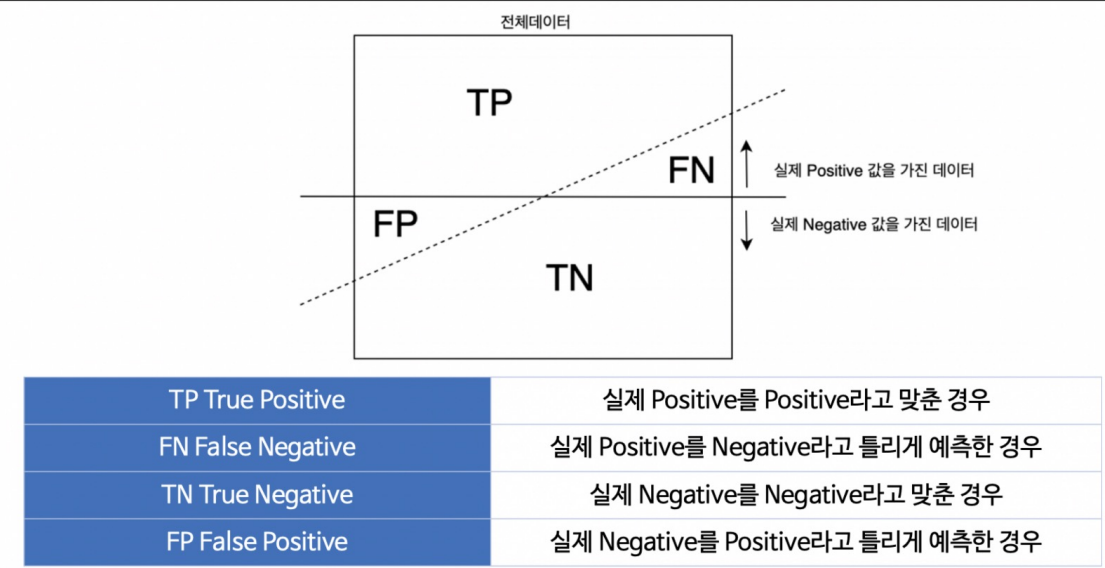 | 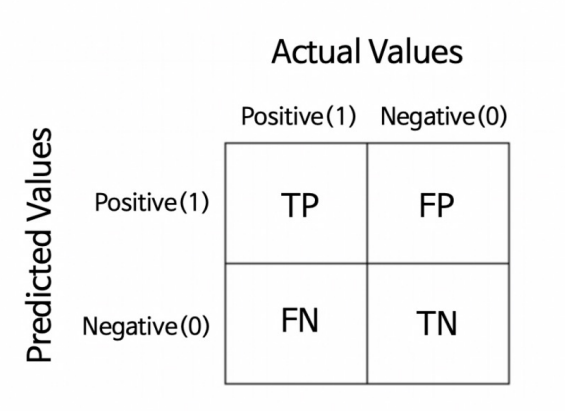 |
|---|
예측의 결과에 따라 4가지로 구분할 수 있다.
좀 쉽게 이해하자면 실제값을 True/False로 예측값을 Positive/Negative라고 분류한다.
정확도(Accuracy)
이때 정확도는 아래와 같이 표현된다.
전체 중에 실제로 맞춘 값의 비율로 익히 많이 사용해왔었다.
=
정밀도(Precision)
정밀도는 1(positive)이라고 예측한 것중 실제로 1(positive)이였던 값의 비율이다.
=
Precision이 자주 사용되는 예는 <스팸 메일>이다.
스펨 메일이 많이 쌓여있는 것은 문제가 안된다.
하지만 스팸 메일이라고 분류한 것들 중에 중요한 메일이 섞여 들어가있다면 문제가 된다.
이처럼 positive라고 예측한 것중 실제로 positive라고 예측하는 것이 중요한 분석에서는 Precision을 많이 사용한다.
재현율(Recall)
재현율은 실제로 참(True)인 데이터들 중 참(True)이라고 예측한 데이터의 비율이다.
=
Recall은 놓쳐서는 안되는 일을 체크해야될 때 자주 사용된다.
예를 들어 환자들이 암 검사를 받으러 왔는데
암 환자가 아닌 사람들을 암이라고 진단하는 것은 다시 검사해서 아니라고 하면 되지만,
암 환자인 사람들을 암이 아니다라고 진단하는 것은 문제를 일으킬 수 있다.
이처럼 실제로 참(True)인 데이터들 중 참(True)이라고 예측하는 것이 중요한 분석에는 Recall이 모델의 성능을 평가하는 중요한 지표가 될 것이다.
Fall-Out
실제로 1(positive)가 아닌데, 1(positive)이라고 예측한 값의 비율이다.
=
지금까지 분류 모델을 적용한 분류기들은 해당 클래스에 속할 확률을 반환하여 어떤 클래스에 속하는지 분류했다.
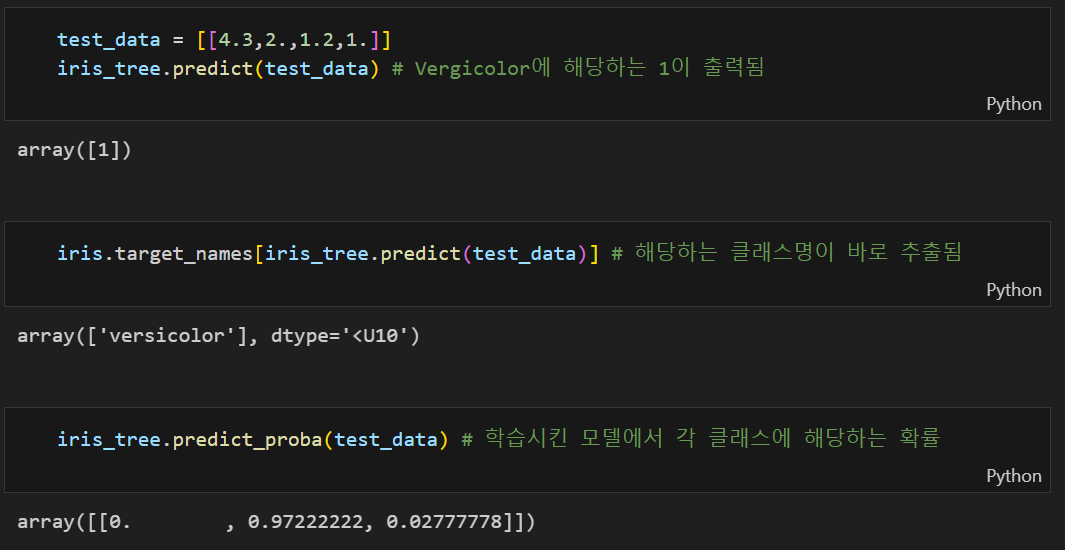 iris 데이터 iris 데이터 | 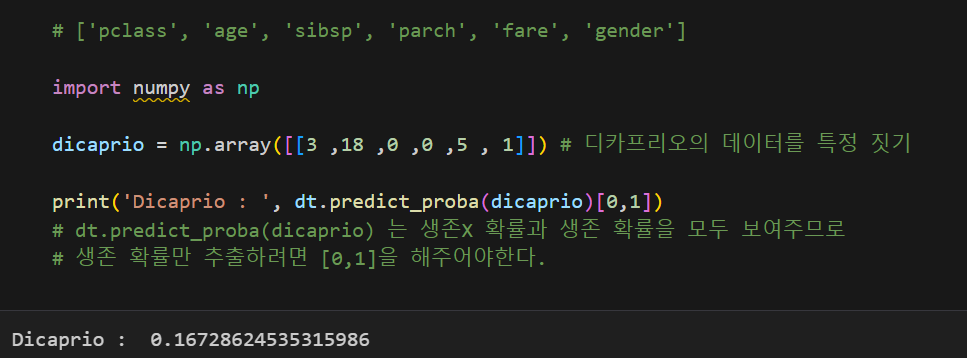 타이타닉 데이터 타이타닉 데이터 |
|---|
예를 들어 iris 데이터의 경우 가장 높은 확률값이 있는 클래스를 해당 값이라고 하고
타이타닉 데이터에서는 0.5를 기준으로 그 결과보다 높으면 살아남고(1), 낮으면 살아남지 못한다(0)고 분류했다.
여기에서 기준이 되는 0.5 와 같은 값을 threshold라 한다.
그렇다면 threshold에 따라서 각 모델 평가 지표의 값들도 달라질 수 있지 않을까? 란 생각을 하게 된다. 한 번 살펴보자.
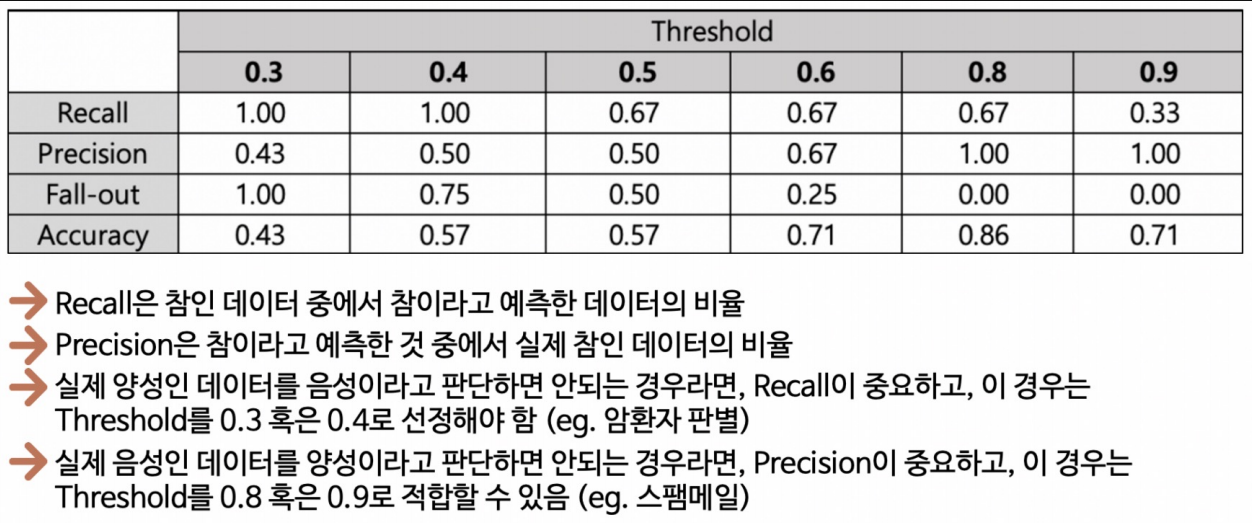
여기에서 알 수 있는 것은 threshold가 0.5인 것이 무조건 좋다!라고 판단할 수 있는건 아니라는 사실이다.
게다가 각 지표들(특히, Recall과 Precision)은 서로 영향을 받으므로 한 지표만 보고 극단적으로 threshold를 높이거나 낮추는 것도 좋은 방법은 아니다.
그렇다면 Recall과 Precision을 한 번에 확인할 수 있는 지표는 없을까?
F1-score
그것이 바로 f1-score이다.
=
f1-score를 사용하면 recall과 precision이 어느 한 쪽으로 치우치지 않고 둘 다 높은 값을 가질수록 높은 값을 가지는 지표로 사용되므로 자주 사용되는 지표 중 하나이다.
ROC 곡선
FPR(False Positive Rate : fallout)이 변할 때 TPR(True Positive Rate : Recall)의 변화를 그린 그림으로 FPR이 x축, TRP이 y축에 위치한다.
ROC 곡선이 직선에 가까울수록 머신러닝 모델의 성능이 떨어지는 것으로 판단하고 위로 볼록한 그래프가 그려질수록 잘 구분하고 있는 모델이다라고 생각할 수 있다.
AUC
이때 ROC 곡선 아래의 면적을 AUC 라고 하는데
ROC가 위로 볼록할수록 좋은 모델이라고 했으니, AUC가 1에 가까울수록 좋은 모델이다라고 할 수 있다.
또한 ROC 곡선이 직선이면 모델의 성능이 떨어지는 것이므로 AUC가 0.5 보다는 커야 유의미한 결과를 내는 모델이라고 판단할 수 있다.
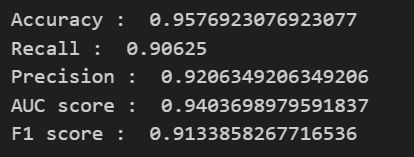
앞서 실습한 와인 데이터를 이용해 각 모델 평가 수치를 구해보자면 아래와 같이 구할 수 있다.
from sklearn.metrics import accuracy_score, precision_score
from sklearn.metrics import recall_score, f1_score
from sklearn.metrics import roc_auc_score, roc_curve
print('Accuracy : ', accuracy_score(y_test, y_pred_test))
print('Recall : ', recall_score(y_test, y_pred_test))
print('Precision : ', precision_score(y_test, y_pred_test))
print('AUC score : ', roc_auc_score(y_test, y_pred_test))
print('F1 score : ', f1_score(y_test, y_pred_test))💻 출력
또한 ROC 곡선을 그리기 위해선 FPR, TRP 그리고 threshold 가 필요하다.
# roc 커브 그리기
import matplotlib.pyplot as plt
pred_proba = wine_tree.predict_proba(X_test)[:, 1] # 각 데이터가 클래스에 속하는 확률
fpr, tpr, threshold = roc_curve(y_test, pred_proba)위와 같이 구하고자 하는 값들을 얻어낼 수 있으며 이를 이용해 plot을 그려주면 된다.
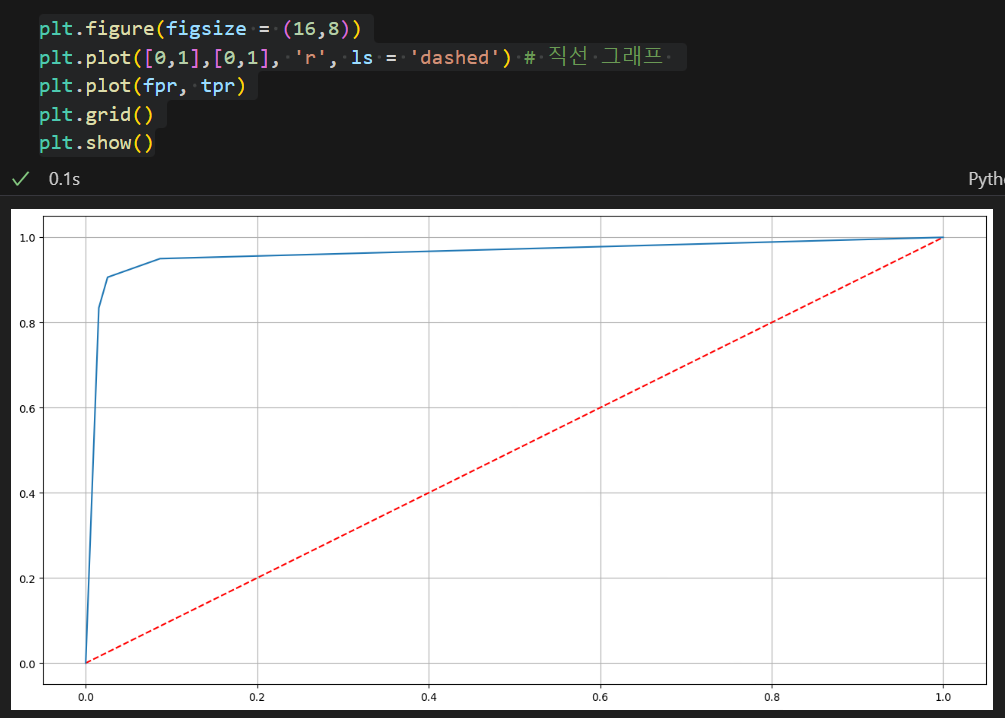
추가적으로 Box plot에 대해 몇 가지 짚고 넘어가보자.
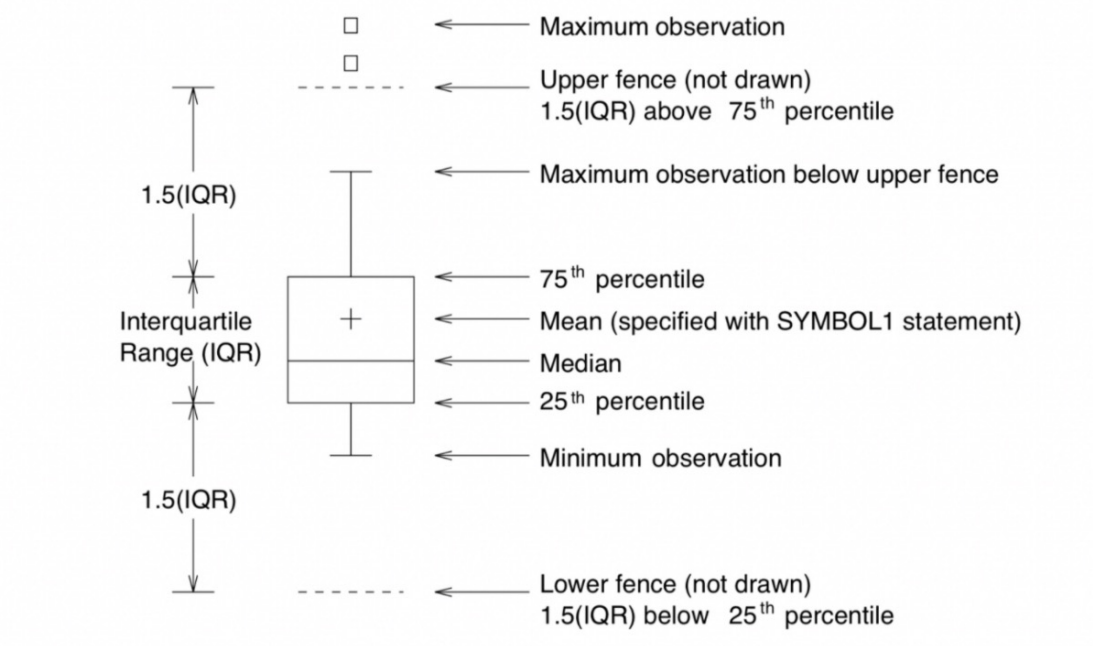
Box plot을 통해 우리는 데이터의 25%, 50%(중앙값), 75%의 지점의 데이터를 추출할 수 있다.
이 데이터들은 우리가 나중에 이상치를 판단할 때 중요한 값이 될수도 있는데 일반적으로 수염 길이는 IQR(Q3 - Q1)의 1.5배로 보고 있다. 따라서 1.5 * IQR 이외의 데이터는 이상치로 판단하고 삭제하는 전처리를 진행할 수도 있다.
실습을 통해 각 값들을 한 번 살펴보자.
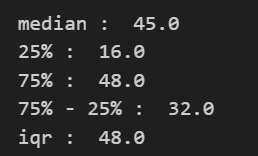
samples = [1,7,9,16,36,39,45,45,46,48,51,100,101]
# 몇몇 지표를 찾는 법
import numpy as np
print('median : ', np.median(samples))
print('25% : ', np.percentile(samples, 25))
print('75% : ', np.percentile(samples, 75))
print('75% - 25% : ', np.percentile(samples, 75) - np.percentile(samples, 25))
iqr = np.percentile(samples, 75) - np.percentile(samples, 25)
print('iqr : ', iqr*1.5)💻 출력
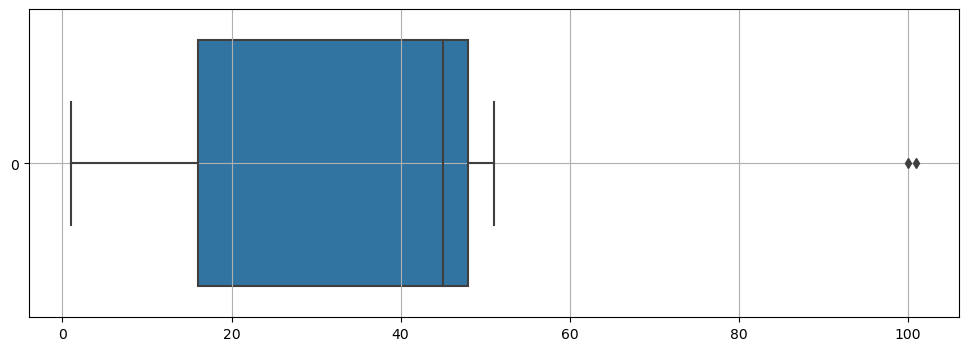
import seaborn as sns
plt.figure(figsize=(12,4))
sns.boxplot(samples, orient='h')
plt.grid()
plt.show()💻 출력
그냥 boxplot을 그려보았을 때도 이상치가 찍히는 것을 볼 수 있다.
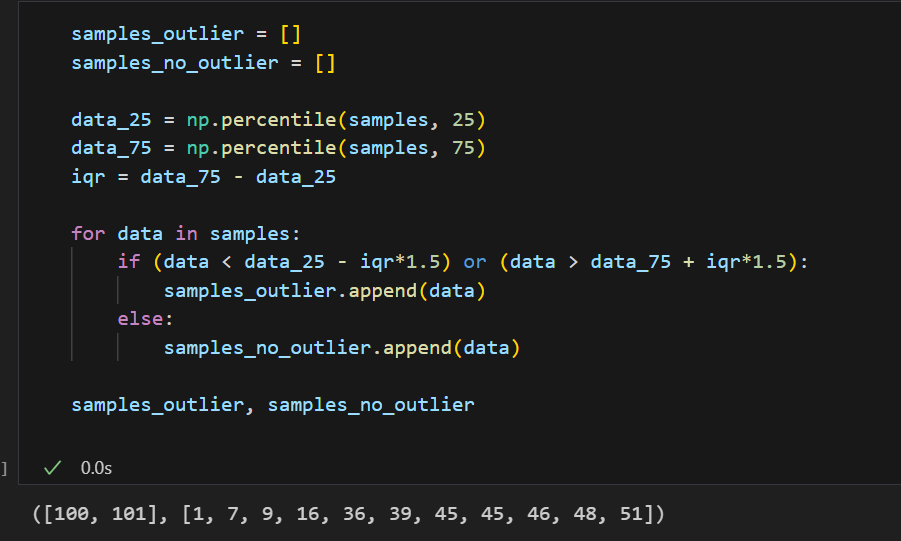
25% 지점으로부터 1.5 * IQR 작은 값과 75% 지점으로부터 1.5 * IQR 많은 값에 속하는 데이터를 이상치로 판단하므로 위와 같이 100, 101을 이상치임을 알 수 있다.
지난 시간까지 지도 학습의 분류(Classification)를 실습해보았다. '지도학습'은 학습을 시킬 때 정답지까지 같이 주고 학습시키는 것을 말하며 '분류'는 어떤 범주형 타겟 데이터에 대해 맞다/아니다를 말해주는 것이다.
회귀(Linear Regression)는 타겟 데이터가 연속된 숫자값인 데이터들을 말한다.
Linear Regression
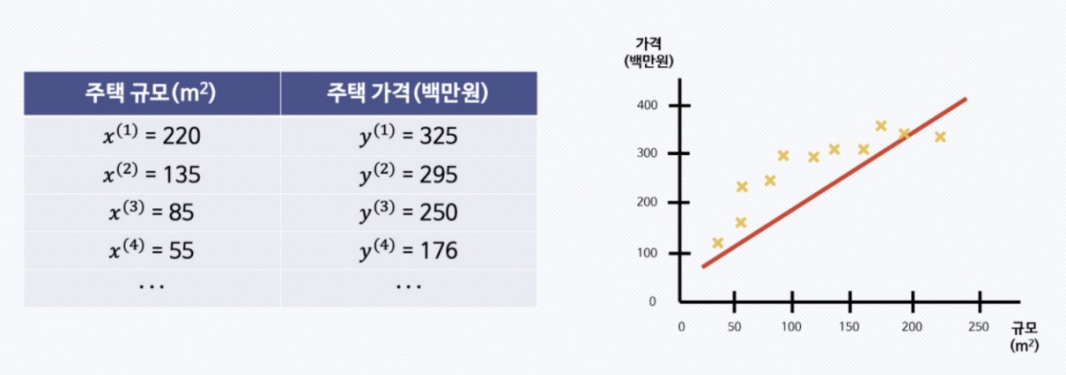
예를 들어 주택의 넓이와 가격이라는 데이터가 있고 주택 가격을 예측하라는 문제가 주어진다면, 우리는 지도 학습의 회귀 문제이구나 라고 생각할 수 있다.
그렇다면 주어진 데이터의 실제값과 예측값의 차이가 최소가 되는 모델을 찾는 것이 우리의 목표가 될 것이다.
이것이 바로 회귀의 OLS(Ordinaray Linear Least Square) 방법이다.
OLS(Ordinaray Linear Least Square, 최소제곱법)
최소제곱법은 실제값과 예측값 차이(=오차, 잔차)의 제곱 합이 최소가 되는 해를 구하는 방법이다.
이를 이용해 회귀 직선을 구해주는 모듈이 statsmodels.formula.api 이다.
import pandas as pd
data = {
'x' : [1,2,3,4,5],
'y' : [1,3,4,6,5]
}
df = pd.DataFrame(data)
# 선형회귀분석
import statsmodels.formula.api as smf
# formula = 'y값 ~ x값' , data = 데이터프레임
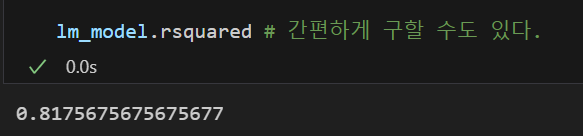
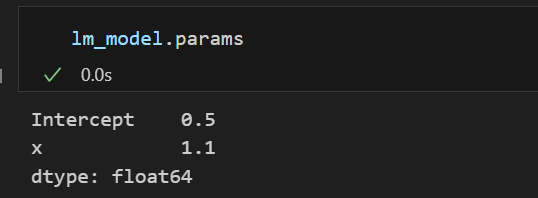
lm_model = smf.ols(formula='y ~ x', data = df).fit()구해진 lm_model의 params를 구해보면 기울기와 절편을 알아낼 수 있다.
잔차 평가
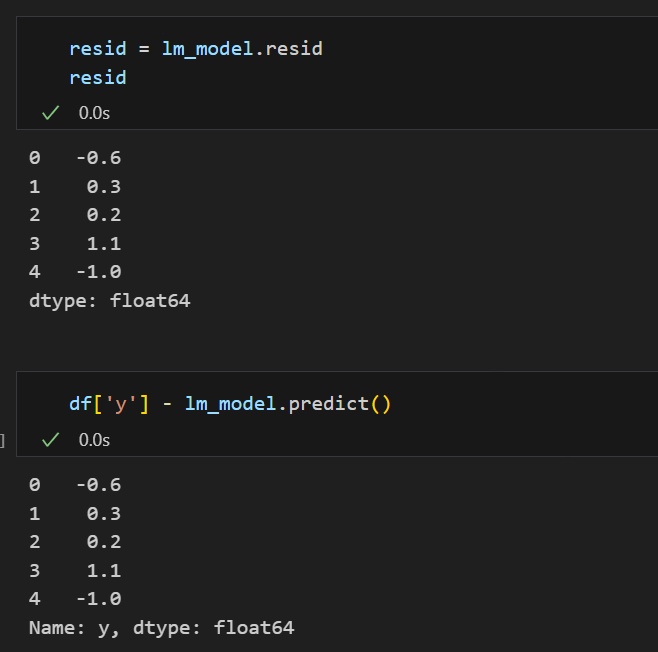
잔차란, 실제값과 예측값의 차이이다.
앞서 얘기를 안 한 것이 있는데 회귀 분석을 하기 위해선 변수들이 정규분포를 가진다는 가정이 전제되어야한다. 정규분포를 가지지 않고 한쪽으로 치우친다면 정확한 결과를 기대하기 힘드므로 만약 정규성을 가지지 않는 데이터라면 정규성을 가지도록 전처리 후 회귀 분석을 진행해야한다.
그러므로 잔차도 평균이 0인 정규분포를 따르는 것이여야 한다. 그래서 이를 확인하는 과정이 필요하다.
결정계수
=
실제값들이 가지는 평균으로부터 예측값들의 차이 제곱합과 평균으로부터 실제값의 차이 제곱합으로 예측값과 실제값이 일치하면 결정계수는 1이 된다.
즉 결정계수가 높을수록 좋은 모델이라 할 수 있다.
import numpy as np
mu = np.mean(df['y'])
y = df['y'] # 실제값
y_hat = lm_model.predict() #예측값
np.sum((y_hat - mu)**2) / np.sum((y - mu)**2) # 직접 계산할 수도 있고
# lm_model.rsquared # 간편하게 구할 수도 있다.💻 출력
통계적 회귀
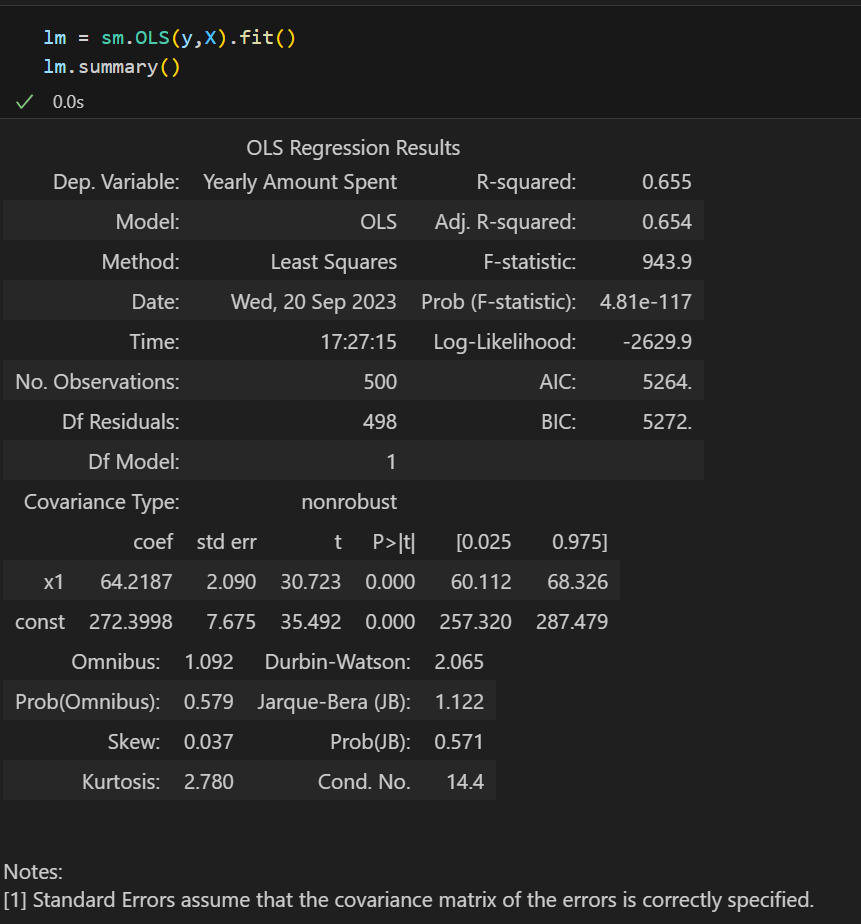
수치적 의미를 좀 더 살펴보자..
.summary()를 이용하면 각 통계적 값들과 Notes에는 해당 모델에 대한 부가 설명도 해준다.
- R-squared : 모형 적합도, y의 분산을 각각의 변수들이 약 65.5%로 설명할 수 있음
- Adj.R-squared : 독립변수가 여러 개인 다중회귀분석에서 사용
- Prob.F-Statistic : 회귀모형에 대한 통계적 유의미성 검정
이 값이 0.05 이하라면 모집단에서도 의미가 있다고 볼 수 있다 - AIC : 주어진 데이터셋에 대한 통계 모델의 상대적인 품질을 평가하는 것으로 최소의 정보 손실을 갖는 모델이 무엇인지 평가해준다. 결정계수는 '평균'을 이용해서 너무 믿으면 안되지만, AIC는 평가하는 지표가 아예 다르므로 어느정도 모델 평가에 사용되는 지표이다.
AIC 값이 낮을수록 좋은 모델이라고 사용된다.
Cost Function
Cost Function은 실제값과 예측값의 차이(= 에러)를 계산한 식이므로, 값이 최소가 될수록 좋은 것이다.
에러를 구한 식을 가지고 그 식이 최소값이 되도록하는 값을 찾는 것이 우리의 일이다.
⬇️ Cost Function 과 Gradient Descent에 대한 정리
https://bigdaheta.tistory.com/85
구글링을 하다가 잘 정리된 링크를 하나 발견해서 같이 첨부해둔다.
만약 에러를 계산한 식이 찾아졌다면 우리는 그것을 미분(또는 편미분)하여 그 식이 0이 되는 해를 찾는 것이 최소값을 찾는 방법이라는 것을 안다.
이때 도움이 되는 파이썬 모듈 sympy를 잠깐 소개해보겠다.
#!pip install sympy #미적분과 같은 수치적계산을 도와주는 모듈
import sympy as sym
theta = sym.Symbol('theta') #'theta'라는 변수다~ 라는 것을 말해주고
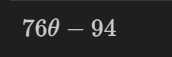
diff_th = sym.diff(38*theta**2 - 94*theta + 62, theta) # diff(미분)하고 싶은 식을 넣어주면
diff_th # 미분식이 반환됨
## poly1d를 통해 식을 써주는 방식도 있지만 sympy 모듈이 훨씬 수치적계산에 도움을 줌💻 출력
예를 들어, 라는 식의 최소값을 찾아야한다면 우리는 해당 식의 미분식을 찾아 그 식이 0이되는 를 찾을 것이다.
이를 sympy 모듈을 통해 (poly1d보다 훨씬) 쉽게 찾을 수 있다.
하지만 이렇게 미분을 하고 최소값을 찾고 하는 과정은 계산이 복잡해지는건 당연한 일일 것이다.
Cost Function의 최소값을 간편하게 구할 수 있는 방법은 없는 것일까??
Gradient Descent
앞서 링크에서 약간의 스포가 되었겠지만 😆 Gradient Descent(경사하강법) 이라는 것이 있다.
그냥 잠깐 간단하게 경사하강법에 대한 알고리즘만 간단하게 소개하자면 아래와 같다.
예를 들어 오차를 표현한 식이 라고 나왔다고 하자.
- 그럼 이때 랜덤하게 어느 한 점()을 잡고 그 임의의 점에서 미분(또는 편미분)값을 계산해서 그 값을 저장해둔다.
우리는 미분값이 0이 되어야 그 지점이 최소값이라는 것을 안다.
그러므로
미분값이 양수라면 처음에 잡은 점()에 미분값 * 만큼 뺀 그 지점에서 다시 미분값을 구해보고
만약 미분값이 음수라면 미분값 * 만큼 더한 그 지점에서 다시 미분값을 구해보자.
- 방법2를 반복하여 미분값이 0에 가까워지는 지점을 찾는다.
이렇듯 미분값을 통해 우리가 어느 부분을 좀 더 살펴보아야할지 방향을 정하는 것을 Gradient Descent라 한다.
이때 미분값 * 만큼 더하고 뺀다고 했는데 는 Learning Rate(학습률)이라고 부른다.
Learning Rate(학습률)이 작으면 최소값을 찾으러가는 간격이 작게 되면서 여러번 업데이트를 해야되서 계산량은 증가하지만 최소값에 잘 도달할 수 있을지도 모른다.
반면 Learning Rate(학습률)이 크면 최소값을 찾으러가는 간격이 커지면서 업데이트 횟수는 적어질 수 있으나 최소값을 찾지 못하고 계속 최소값 부근에서 0에 가까워지는 값을 찾지 못하고 헤맬 수( = 진동할 수)도 있을 것이다.
따라서 Learning Rate(학습률) 또한 적당한 값을 찾아야하는 Hyperparameter 중 하나이다.
다변량 회귀(e.g. Boston data)
타겟 데이터를 예측할 때 사용되는 X 의 변수 개수가 2개 이상인 것을 다변량 회귀라고 한다.
Boston 집 값 예측 데이터를 통해 한 번 살펴보자.
from sklearn.datasets import load_boston
boston = load_boston()
boston.keys()💻 출력
ImportError:
load_bostonhas been removed from scikit-learn since version 1.2.
현재 버전이 업데이트되면서 해당 데이터 로드가 삭제되었다.
Boston 데이터를 읽을 수 있는 방법은 많지만, 공식 사이트를 참고해보자.
위 코드를 통해 읽어들이면, X와 y에 각각 데이터가 저장된다.
이때 y가 우리의 타겟 데이터 집 값 데이터이다.
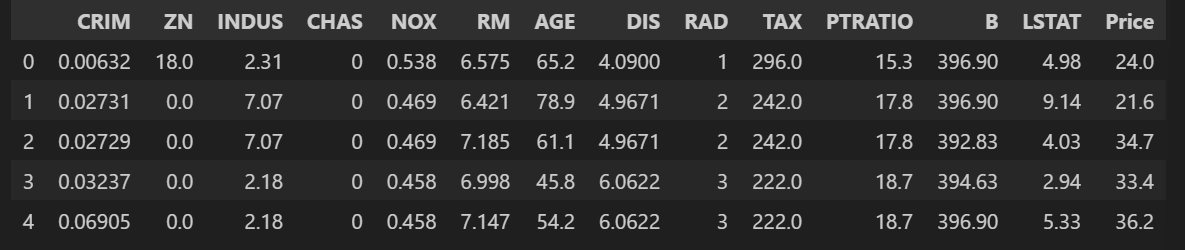
하지만 EDA를 해보기 위해 두 데이터를 하나의 데이터프레임으로 만들어주었다.
# 한 데이터프레임으로 만들기 위한 작업
boston_pd = X
boston_pd["Price"] = y # 타겟데이터
boston_pd.head()💻 출력
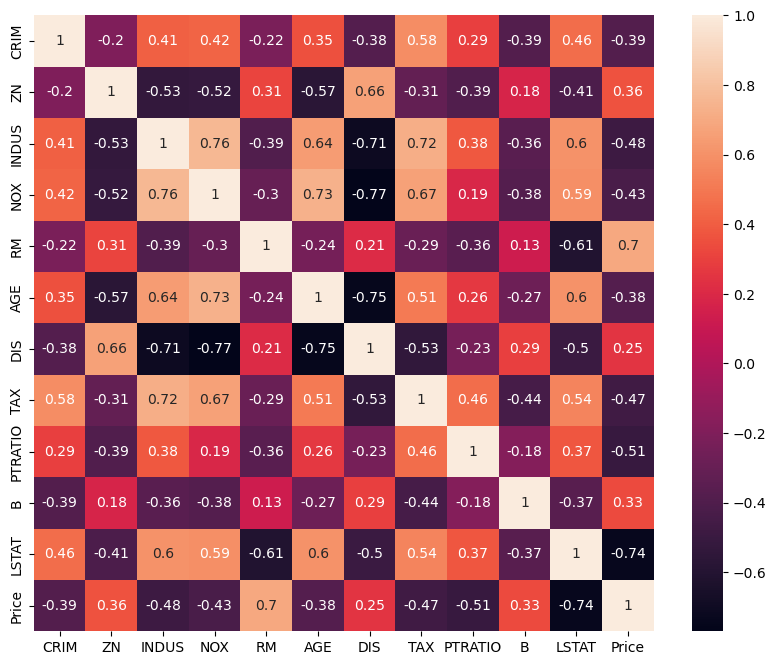
# 상관계수
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(10,8))
sns.heatmap(boston_pd.corr(), annot=True)💻 출력
상관계수를 살펴보면 RM, LSTAT 컬럼이 Price 컬럼과 높은 상관관계를 가지는 것 같다.
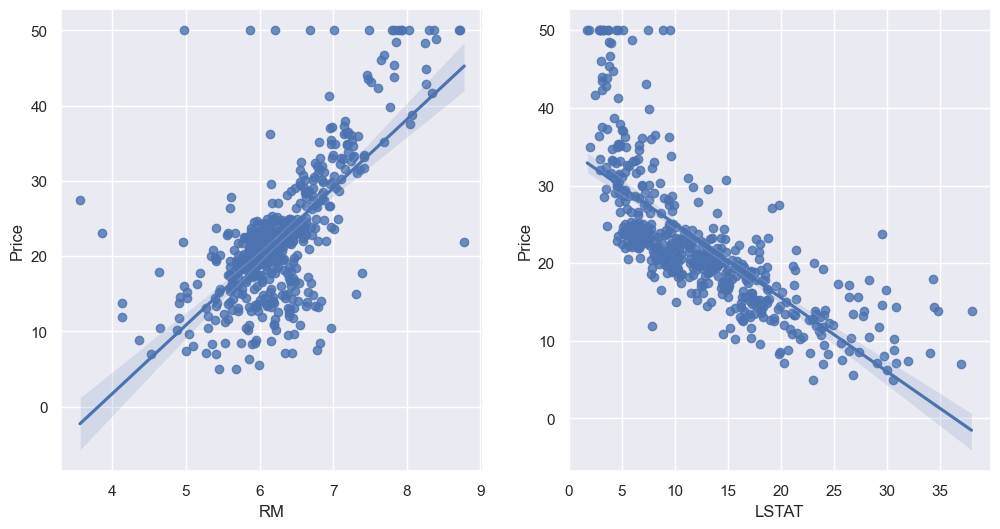
두 컬럼과의 관계를 좀 더 살펴보자.
산점도, 회귀선, 신뢰 구간을 동시에 표현해주는 regplot 을 통해 그려보았다.
sns.set_style('darkgrid')
sns.set(rc = {'figure.figsize' : (12, 6)})
fig, ax = plt.subplots(ncols = 2)
sns.regplot(x = "RM", y = "Price", data = boston_pd, ax = ax[0])
sns.regplot(x = "LSTAT", y = "Price", data = boston_pd, ax = ax[1])💻 출력
대체적으로 RM이 커질 수록 Price가 오르고 LSTAT가 작을수록 Price가 크긴한데 특이한 데이터가 몇 개 보이기도 한다.
LSTAT 컬럼은 저소득층의 비율이다.
생각해보자. 저소득층들은 집 값이 적은 곳에서 거주를 할텐데, 어찌보면 LSTAT을 함께 넣어 분석하는 것은 너무 뻔한 이야기가 아닐까?
물론 Boston 데이터에서 해당 컬럼을 빼고, 넣는거에 성능이 크게 달라지진 않지만 앞으로 우리가 분석할 데이터에 이런 상황을 마주하게 된다면 고민이 좀 더 필요할 것이다.
# 모델에 넣으려면 숫자형이여야하므로 'CHAS', 'RAD' 데이터유형 변경
boston_pd['CHAS'] = boston_pd['CHAS'].astype('float')
boston_pd['RAD'] = boston_pd['RAD'].astype('float')
boston_pd.info() |  |
|---|
모델링을 하기 위해 데이터 변형을 해주었다.
from sklearn.model_selection import train_test_split
X = boston_pd.drop('Price', axis = 1)
y = boston_pd['Price']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=13)
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(X, y)
import numpy as np
from sklearn.metrics import mean_squared_error
pred_tr = reg.predict(X_train)
pred_test = reg.predict(X_test)
rmse_tr = np.sqrt(mean_squared_error(y_train, pred_tr))
rmse_test = np.sqrt(mean_squared_error(y_test, pred_test))
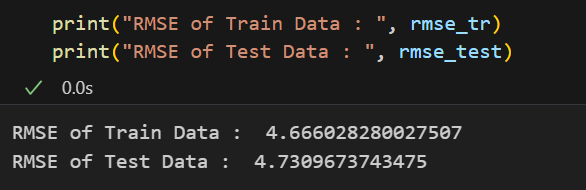
print("RMSE of Train Data : ", rmse_tr)
print("RMSE of Test Data : ", rmse_test) 💻 출력
regression은 분류문제와 같이 accuracy 같은 것이 없기 때문에
regression에 맞는 모델 성능 지표를 써야한다. 대표적인 것이 rmse이므로 rmse를 통해 모델 성능을 평가해보았을 때 위와 같았다.
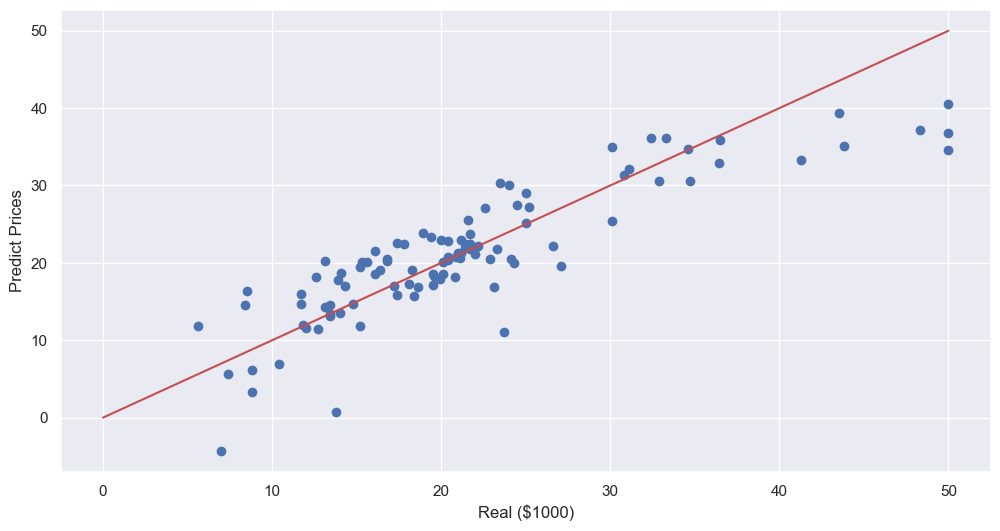
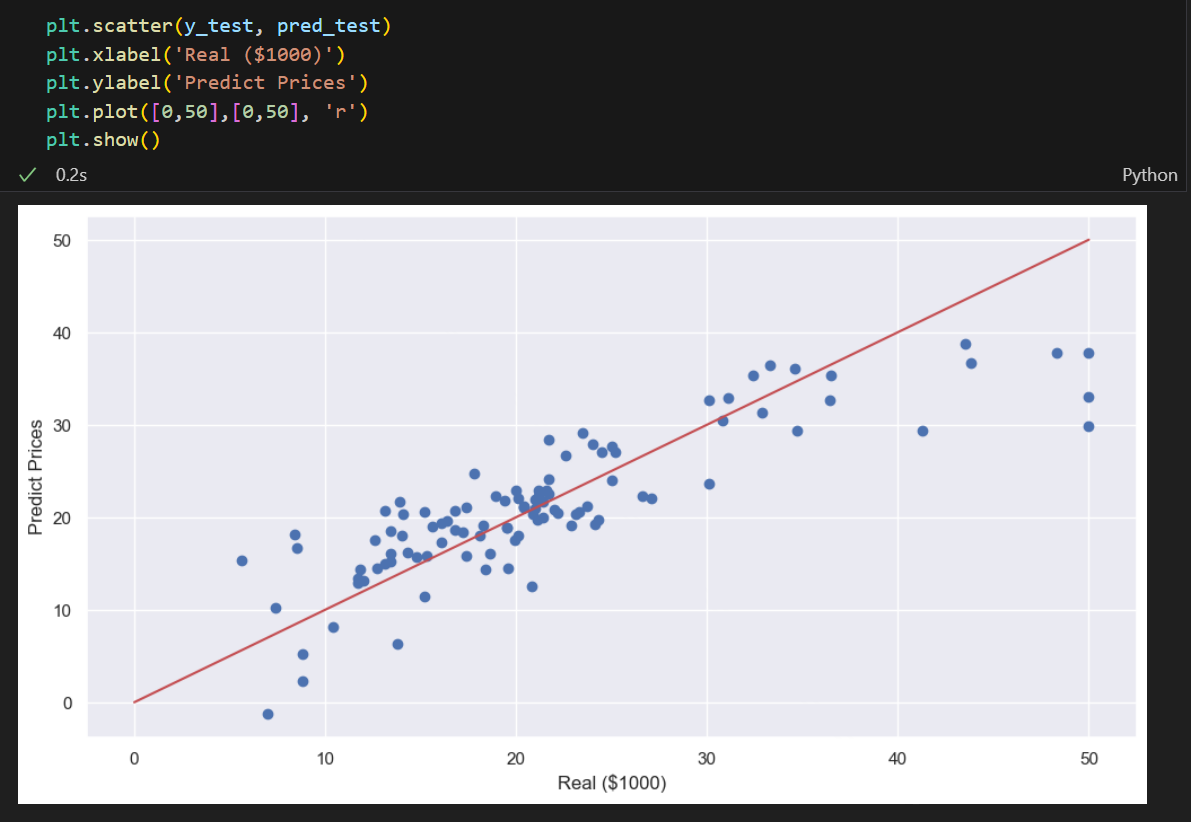
plt.scatter(y_test, pred_test)
plt.xlabel('Real ($1000)')
plt.ylabel('Predict Prices')
plt.plot([0,50],[0,50], 'r')
plt.show()💻 출력
실제값과 예측값을 시각화해보면 위와 같은데, 오른쪽 상단 부분이 사알짝 안 맞는 것으로 보인다.
이는 또 앞으로 우리가 배울 여러가지 내용들을 통해 데이터에 잘 맞는 모델을 만들어야할 것이다.
-번외-
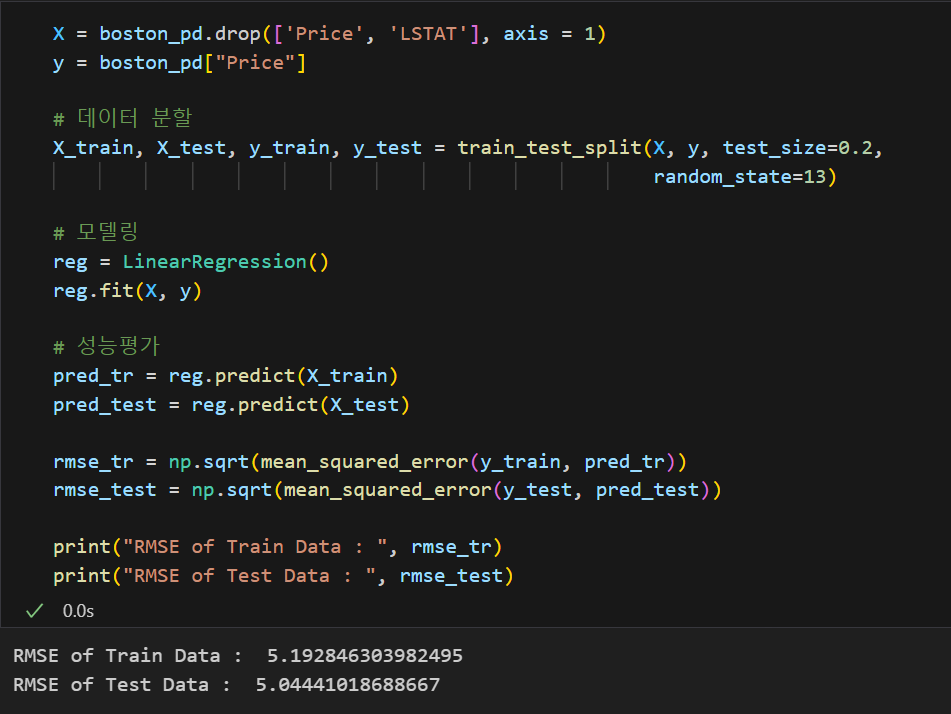
LSTAT 컬럼을 삭제하면 모델의 성능이 높아질까?
 |  |
|---|
결론만 보았을 때는 RMSE가 높아진 것으로 보아 모델의 성능은 나빠진 것으로 보인다.
하지만 모델의 성능 지표가 RMSE 하나가 아니기 때문에 위 결과 하나 때문에 LSTAT 컬럼은 삭제해야해! 라는 근거는 되지 못한다.