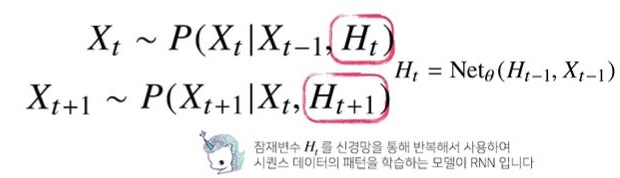[AI 기초] RNN 첫걸음

시계열, 시퀀스 데이터에 적용. IID (독립분포)

시퀀스 데이터 이해하기

• 순차적으로 들어오는 데이터
• 소리, 문자열, 주가 등의 데이터를 시퀀스 데이터로 분류
• 독립 동등 분포(I.I.D) 가정을 잘 위배하기 때문에 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포도 바뀌게 됨
  • Ex) 개가 사람을 물었다 & 사람이 개를 물었다

시퀀스 데이터 다루기

• 이전 시퀀스의 정보로 미래 확률분포를 다루기 위해 조건부 확률을 이용할 수 있음
  • P(X1, ...,Xt) = P(Xt|X1,...,Xt-1)P(X1,...,Xt-1)
  • 베이즈 법칙 이용
  • 
  • Xt ~ P(Xt|Xt-1,...,X1)
    이 조건부확률은 과거의 모든 정보를 사용하지만 시퀀스 데이터를 분석할 때 모든 과거의 정보들이 필요한 것은 아님
  • Ex) 기업주가 예측시 30년치 데이터가 필요하진 않음. 근 5년 ~ 최근 정보만 사용한다는 것, 문장 생성시 앞뒤 맥락만 보면 됨.
• 시퀀스 데이터를 다루기 위핸 길이가 가변적인 데이터를 다룰 수 있는 모델이 필요함.
  • Xt ~ P(Xt|Xt-1,...,X1)
  • Xt+1 ~ P(Xt+1|Xt,Xt-1,...,X1)
• 일정하게 고정된 길이 $tau$만큼의 시퀀스만 사용하는 경우 AR($tau$)(Autoregressive Model) 자기 회귀 모델이라고 부름
• Xt를 구하기 위해 직전 과거의 정보(Xt-1)와 이전 과거(Xt-2,...,X1)인 Ht를 잠재변수로 인코딩하여 3가지의 데이터로 분석하게됨 → 길이 고정
• 장점 : 과거의 모든 데이터를 통해 예측 가능, 가변적인 데이터 길이를 고정함 → 과거 데이터를 어떻게 처리할 것인가 한 것이 RNN
  

RNN(Recurrent Neural Network) 이해하기

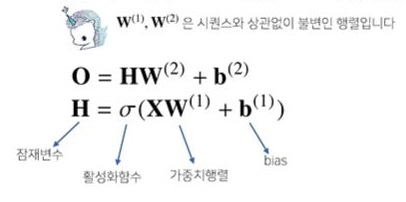
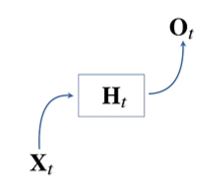
• 가장 기본 RNN 모형은 MLP와 유사한 모양임
  
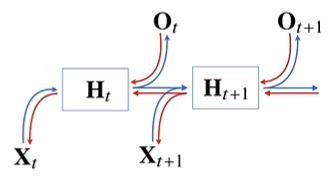
• 잠재변수 H에 선형모델을 결합시켜 출력행렬인 O를 출력 → 하지만 이 모델은 과거의 정보를 다룰 수 없음
  
• 그럼 어떻게 과거 정보를 넣을까?
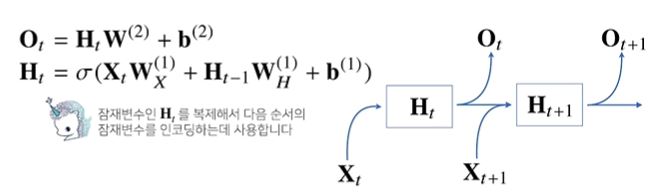
  → 잠재변수인 Ht를 복제해서 다음 순서의 잠재변수를 인코딩할 때 사용함
  
  → 가중치 행렬이 3개가 나옴. Wx(1), WH(1), W(2). 각각의 가중치 행렬은 t에따라 바뀌지 않고, 바뀌는건 Xt, Ht 뿐.
• RNN의 역전파는 잠재변수의 연결그래프에 따라 순차적으로 계산.
  (= X1 ~ Xt로 모든 시점을 계산한 다음 마지막 시점의 gradient가 타고타고 가는 Backpropagation Through Time(BPTT) 사용)
• 역전파시 잠재변수(Ht)엔 gradient 2가지(Ht+1, output)가 들어오게 되고, 이게 이전 잠재변수(Ht-1)와 Xt-1에 영향을 줌
  

BPTT 더 살펴보기

• 
  각 가중치 행렬의 미분 계산
  
  이렇게 되면 최종적으로 나오는 마지막 항을 보면 잠재변수의 미분이 곱해진 후 더해지게 됨. 그럼 시퀀스 길이가 길어질 수록(1~t) 곱해지는 것이 불안정해짐.
  (1보다 크면 미분값이 엄청 커지고, 1보다 작으면 엄청 작아지게될 확률이 높기 때문)

Gradient Vanish의 해결책?

• 과거의 데이터를 소실하기가 쉬움. 따라서 시퀀스의 길이가 길어지는 BPTT의 경우 길이를 끊어주는 것이 필요한데, 이를 truncated BPTT라 함.
• truncated BPTT : 미래 중 몇개는 gradient를 끊고 과거의 정보에 해당하는 몇개의 block을 나눠 역전파를 계산하는 방법
  Ex. Ht에서는 Ot, Ht+1의 값을 받는 것이 아니라, Ot의 값만 받아서 Ht에 전달하는 것
• 하지만 완전한 해결책이 되진 않음 → 길이가 긴 시퀀스는 LSTM, GRU를 사용함
  

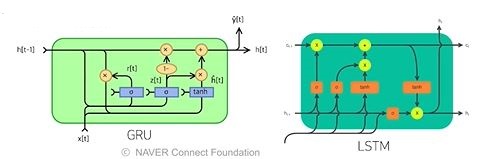
사실 최근엔 기본 RNN보단 LSTM, GRU 같은 진보된 모델 사용함