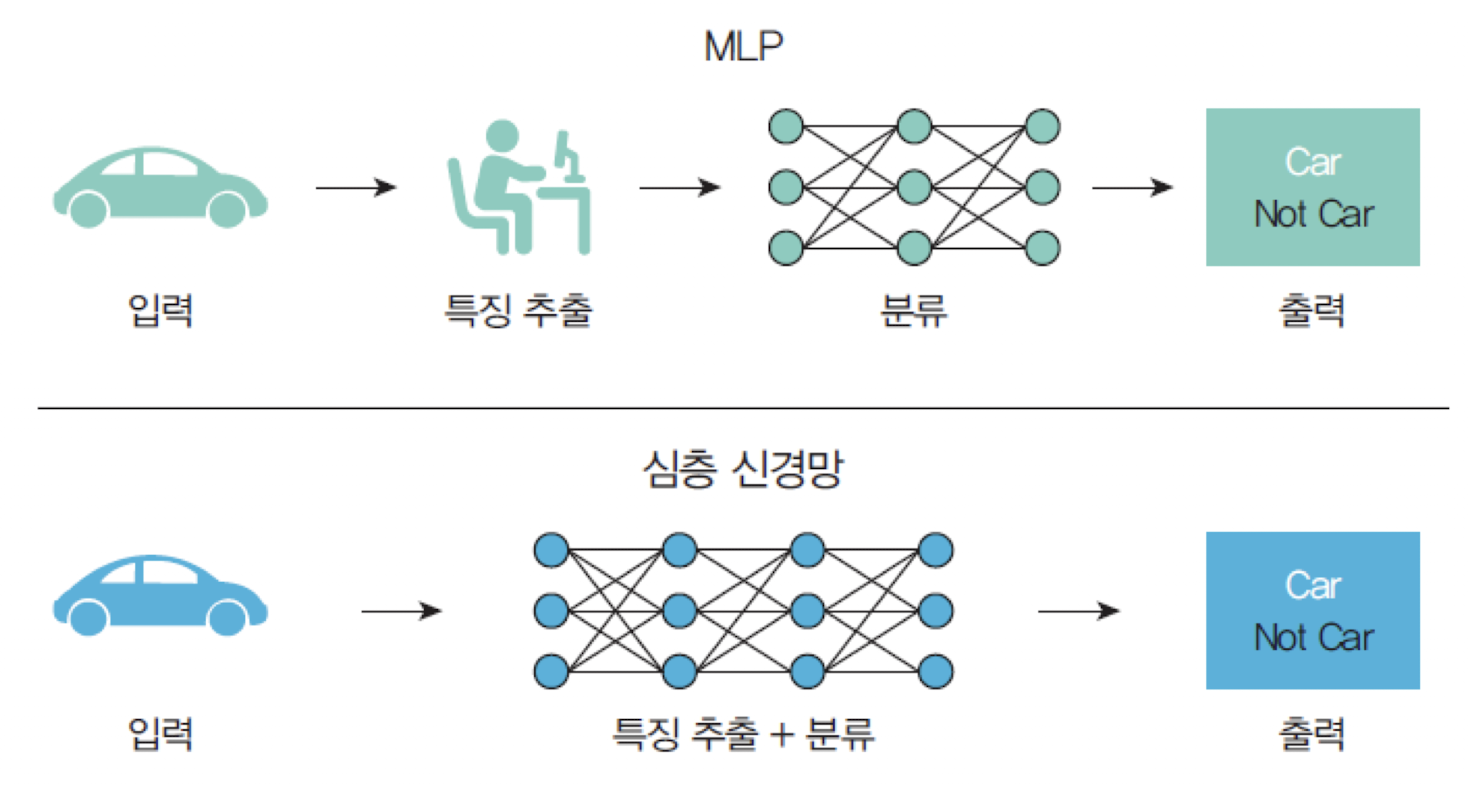
심층 신경망 (Deep Neural Networks)

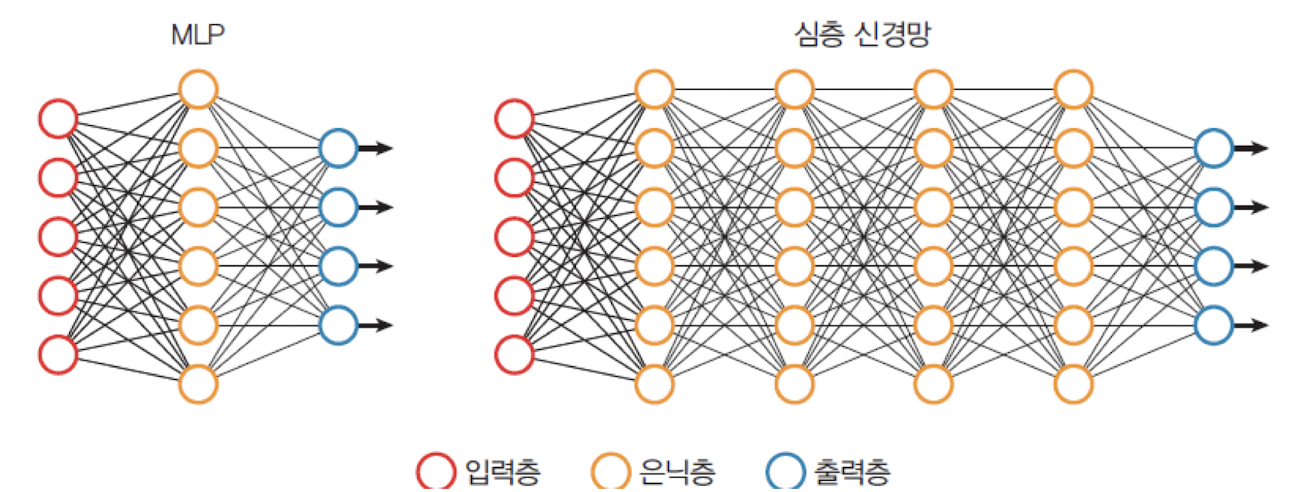
심층 신경망(DNN)은 다층 퍼셉트론(MLP: Multi-Layer Perceptron)의 은닉층을 여러 개 사용한 형태이다. 즉, 단일 은닉층을 넘어서 깊은 구조를 가진 신경망을 의미한다.

• 입력층 → 여러 개의 은닉층 → 출력층 구조
• MLP는 은닉층이 1개이지만 DNN은 은닉층이 다수 존재한다.
• MLP와 DNN은 기본적인 학습 알고리즘(ex. 역전파, 경사하강법)이 동일하다.
• 최근에 딥러닝은 컴퓨터 시각, 음성 인식, 자연어 처리, 소셜 네트워크 필터링, 기계 번역 등에 적용되어서 인간 전문가에 필적하는 결과를 얻고 있다.

---

🤨 MLP의 문제점 해결

• 은닉층이 깊어질수록 그래디언트 소실 문제가 발생한다.
  ➡️ ReLU와 BatchNorm으로 해결

• 훈련 데이터가 부족하면 과적합이 발생하였다.
  ➡️ 정규화와 Dropout 등으로 해결

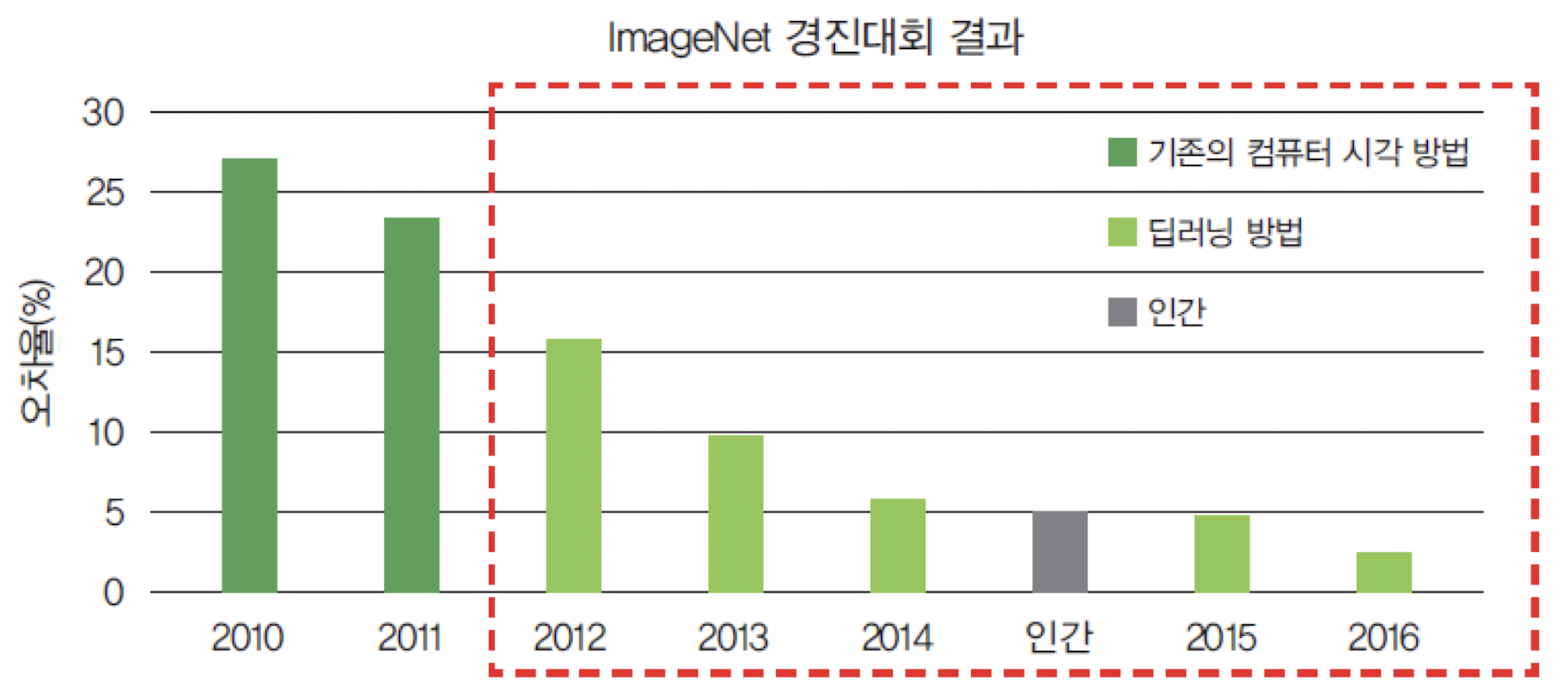
• 2012년 AlexNet이 ImageNet 대회에서 우승하며, 딥러닝 혁명의 시작점이 되었다.

🚑 GPU의 도움

• DNN의 학습 속도는 상당히 느리고 계산 집약적이기 때문에 학습에 시간과 자원이 많이 소모되었다.

• 게이머들의 영향으로 GPU 기술이 발전하면서 GPU의 데이터 처리 기능을 딥러닝이 사용하게 되는 영향이 크게 작용했다.

---

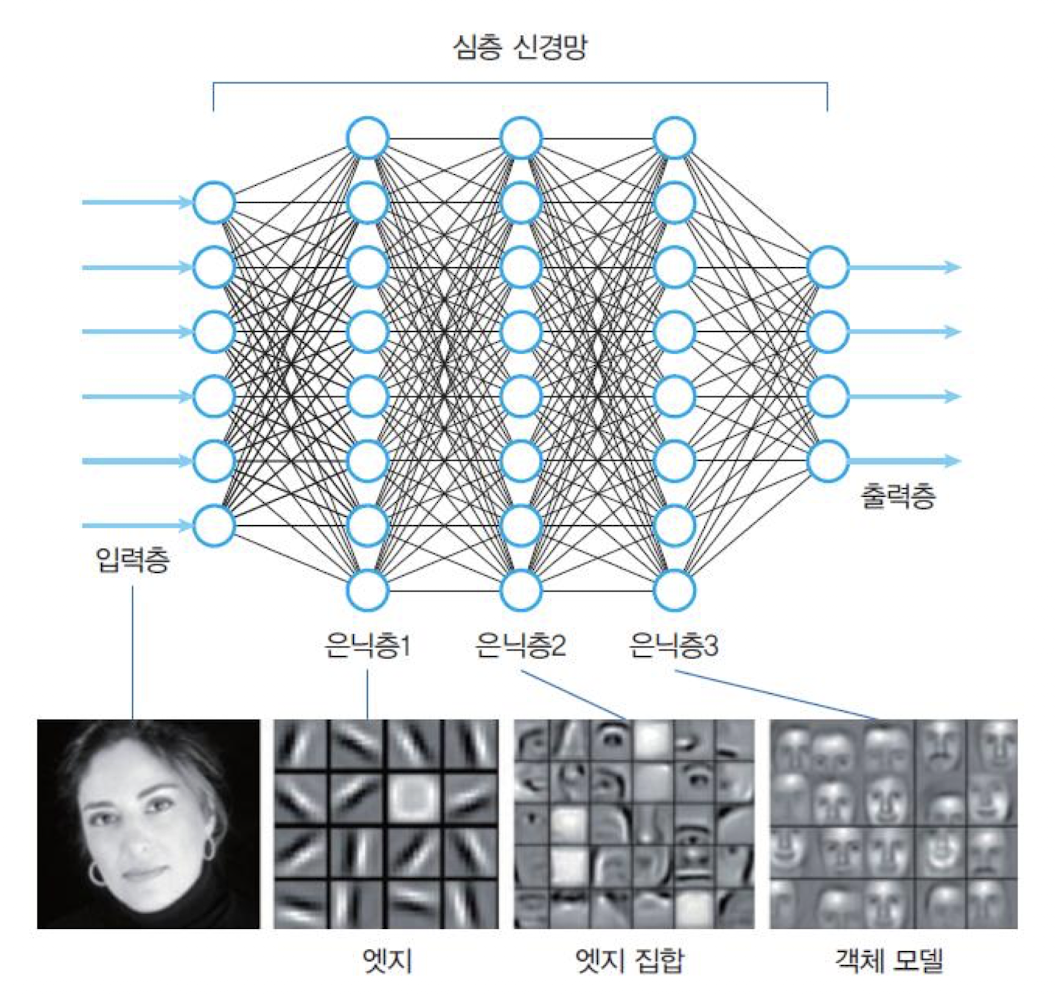
🔗 은닉층의 역할

• 여러 개의 은닉층 중에서 앞단은 경계선(에지)과 같은 저급 특징들을 추출하고 뒷단은 코너와 같은 고급 특징들을 추출한다.

---

🔗 MLP vs DNN

기존 신경망의 문제

• 그래디언트 소실 문제 (Gradient vanishing problem)
• 손실함수 선택 문제 (Loss function selection problem)
• 가중치 초기화 문제 (Weight initialization problem)
• 범주형 데이터 처리 문제 (Categorical data problem)
• 데이터 정규화 문제 (Data normalization problem)
• 과잉 적합 문제 (Overfitting problem)

---

기존 신경망의 문제들

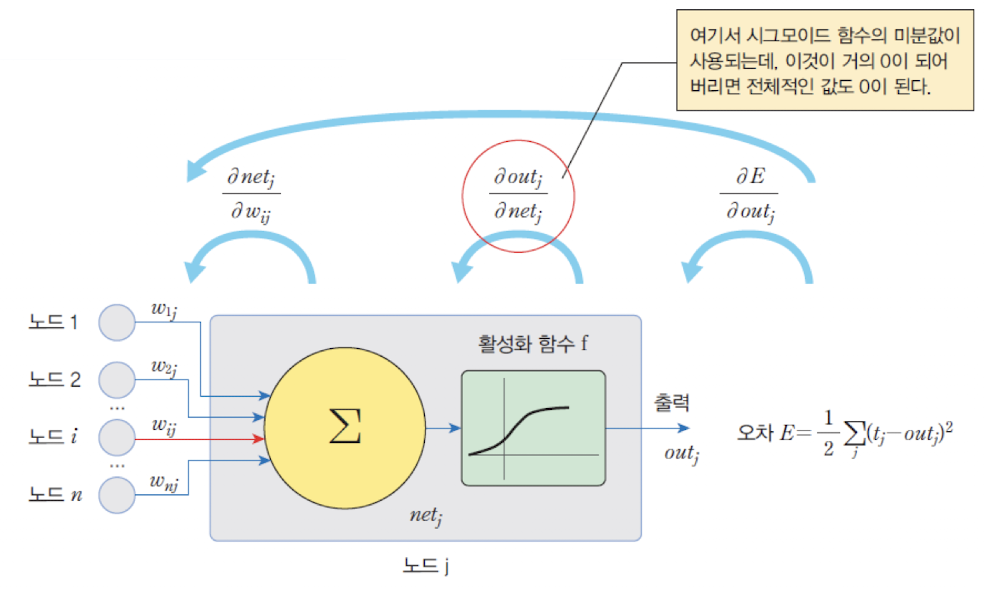
✅ 그래디언트 소실 문제 (Gradient vanishing problem)

• 심층 신경망에서 그래디언트가 전달되다가 점점 0에 가까워지는 현상으로, 출력층에서 멀리 떨어진 가중치들은 학습이 되지 않는다.
• 신경망이 너무 깊기 때문에 남아있는 그래디언트가 거의 없는 현상이 발생한다.

원인

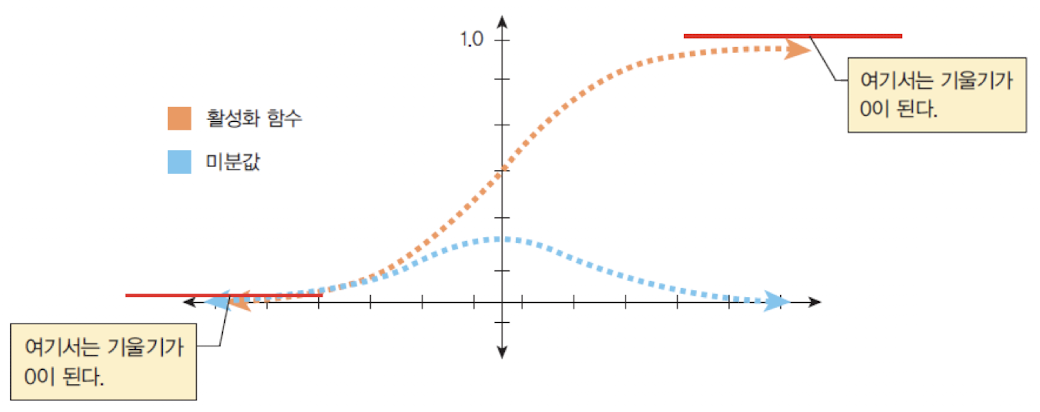
시그모이드(sigmoid) 활성화 함수가 그 원인이 된다.

➡️ 그래디언트는 접선의 기울기, 약간 큰 양수나 음수가 시그모이드 함수에 들어오면 기울기가 거의 0이 됨
➡️ 시그모이드 함수의 미분값은 항상 0에서 1사이, 1보다 작은 값이 여러번 곱해지면 결국 0으로 수렴함

해결방안

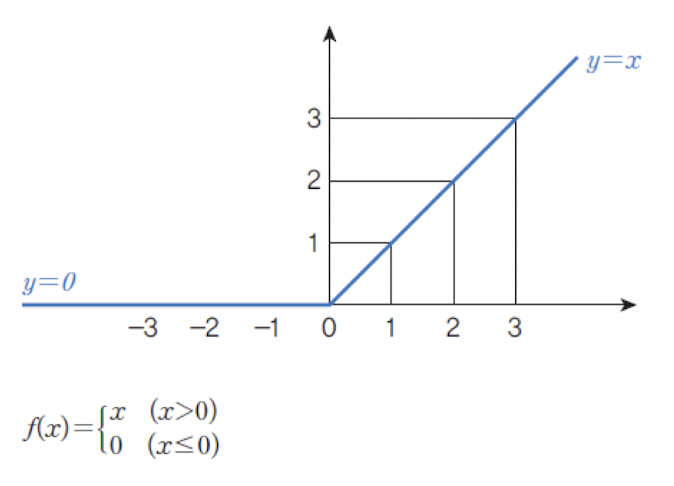
• 활성화함수로 시그모이드(sigmoid) 대신 ReLU 함수를 많이 사용한다.
• ReLU 함수는 입력값을 0과 1사이로 압축하지 않기 때문에, 미분값이 0이 아니면 1이되어 출력층의 오차가 감쇠되지 않고 그대로 역전파 된다.
• 0에서는 미분 불가능하지만 문제되지 않고 속도가 빠르다는 장점이 있다.

---

✅ 손실함수 선택 문제 (Loss function selection problem)

• 기존 손실 함수로는 MSE(평균제곱오차)를 사용하였다.
  $E = \frac{1}{m} \sum \left( y_i - \hat{y}_i \right)^2$ where $m$: 출력 노드의 개수

• 정답과 예측값의 차이가 커지면 MSE도 커지므로 충분히 가능한 손실함수지만, 분류문제를 위해서는 더 성능이 좋은 교차 엔트로피 함수를 많이 사용한다.

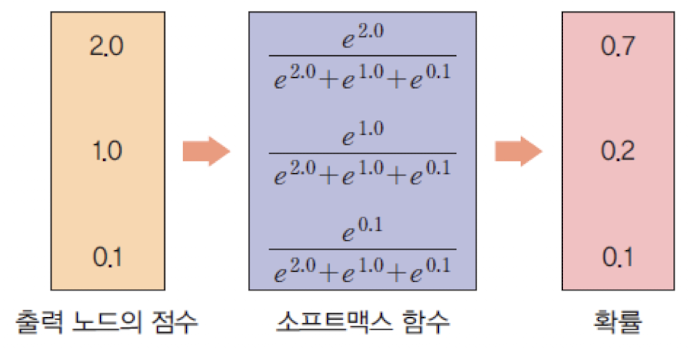
• 이때, 출력층의 활성화 함수로 소프트맥스(softmax) 함수를 사용한다.

소프트맥스(softmax) 활성화 ㅎ마수

• Max 함수의 소프트한 버전
• Max 함수의 출력은 전적으로 최대 입력 값에 의하여 결정됨
• 합이 1 이므로 확률값으로 사용 가능

---

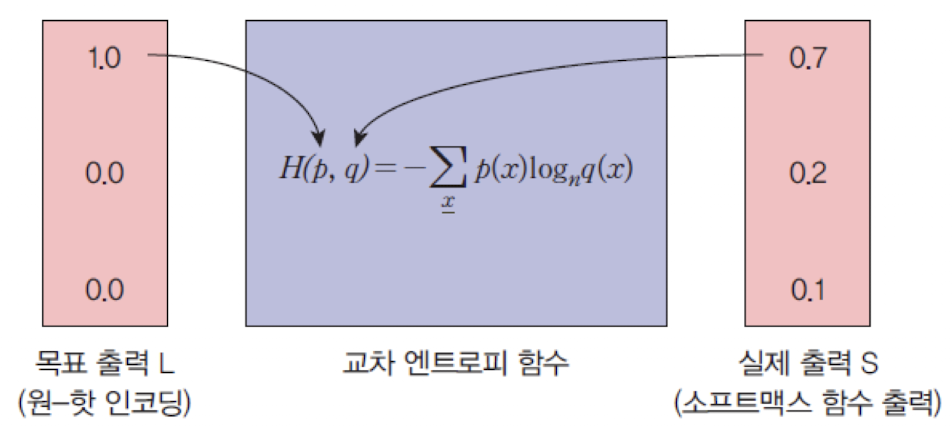
교차 엔트로피 손실 함수 (Cross Entropy Loss function)

2개의 확률 분포 $p, q$에 대하여 다음과 같이 정의된다.

➡️ 목표 출력 확률분포 $p$와 실제 출력 확률분포 $q$ 간의 거리를 측정

`일반적인 계산 식`:

완벽하게 일치한다면:

교차 엔트로피 계산

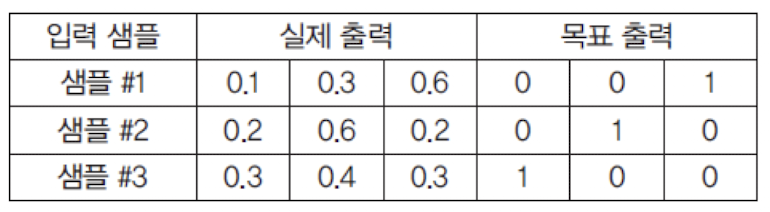
출력 노드가 3개 있는 신경망에서 교차 엔트로피 계산 (각 샘플 별 계산)

• 첫번째 샘플

  $\begin{aligned} H(p, q) &= -\left( \log(0.1) \cdot 0 + \log(0.3) \cdot 0 + \log(0.6) \cdot 1 \right) \\ &= - (0 + 0 + \log(0.6)) \approx 0.51 \end{aligned}$

• 두번째 샘플

  $\begin{aligned} H(p, q) &= -\left( \log(0.2) \cdot 0 + \log(0.6) \cdot 1 + \log(0.2) \cdot 0 \right) \\ &= - (0 + \log(0.6) + 0) \approx 0.51 \end{aligned}$

• 세번째 샘플

  $\begin{aligned} H(p, q) &= -\left( \log(0.3) \cdot 1 + \log(0.4) \cdot 0 + \log(0.3) \cdot 0 \right) \\ &= -(\log(0.3) + 0 + 0) \approx 1.20 \end{aligned}$

• 3개 샘플의 평균 교차 엔트로피 오류 계산 $\frac{0.51 + 0.51 + 1.20}{3} \approx 0.74$

---

평균제곱오차 vs 교차 엔트로피

출력 유닛이 하나인 경우

• 평균 제곱 오차 (MSE)

  $E = (y - \hat{y}_i)^2$

• 이진 교차 엔트로피 (Binary Cross Entropy)

  $E = -\left[ y \log_n (\hat{y}) + (1 - y) \log_n (1 - \hat{y}) \right]$

• MSE

  • 정답이 0일 때, $E = \hat{y}_i^2$

  • 정답이 1일 때, $E = (1 - \hat{y}_i)^2$

• BCE

  • 정답이 0일 때, $E = -\log_n (1 - \hat{y})$

  • 정답이 1일 때, $E = -\log_n (\hat{y})$

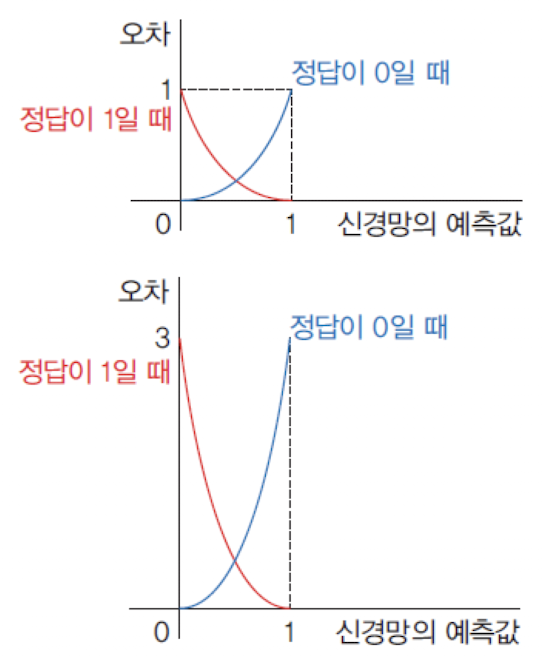
교차 엔트로피의 오차가 MSE의 오차보다 큼을 알수 있다.
미분 값은 더 차이가 나며 이 미분값이 곱해져서 가중치가 변경됨으로 이진 분류문제에서 MSE보다 교차 엔트로피를 사용하는 것이 훨씬 유리

---

Keras에서의 손실함수

BinaryCrossEntropy (BCE)

➡️ 이진 분류 문제를 해결할 때 사용 (ex. 이미지를 "강아지" vs "강아지 아님" 으로 분류할 때)

$\frac{BCE1 + BCE2 + BCE3 + BCE4}{4} \approx 0.345$

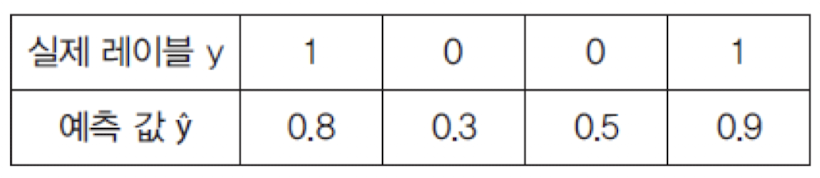
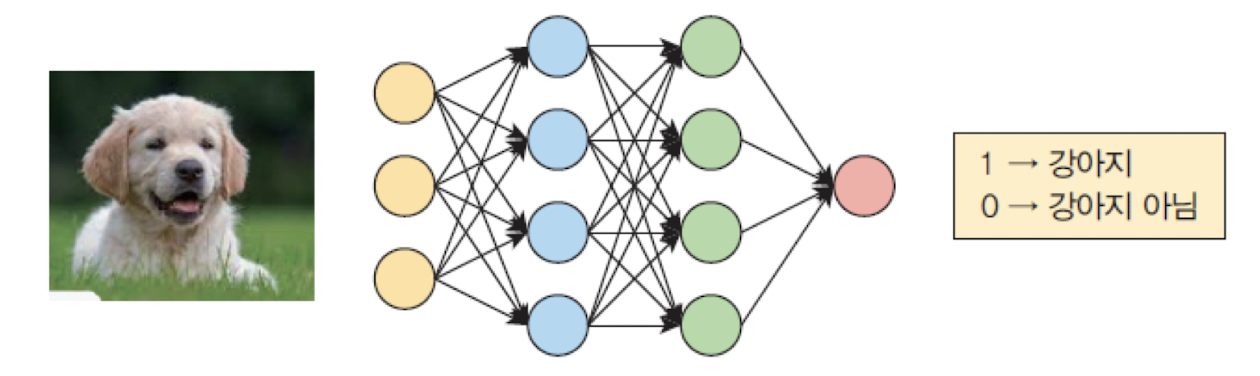
import numpy as np
import tensorflow as tf

y_true = [[1], [0], [0], [1]]
y_pred = [[0.8], [0.3], [0.5], [1.9]]
bce = tf.keras.losses.BinaryCrossentropy()
print(bce(y_tre, y_pred).numpy
# 0.34458154

CategoricalCrossentropy (CCE)

➡️ 다중 분류 분제를 해결할 때 사용 (ex. 이미지를 "강아지" vs "고양이" vs "호랑이" 으로 분류할 때)
➡️ 정답은 onehot 인코딩으로 제공한다.

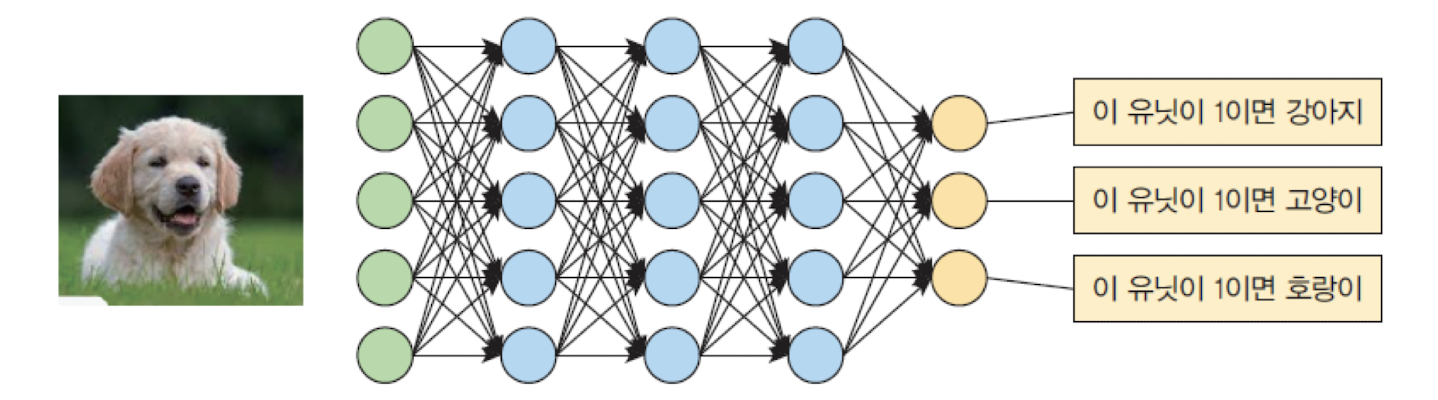
y_true = [[0.0, 1.0, 0.0], [0.0, 0.0, 1.0], [1.0, 0.0, 0.0]] # 고양이, 호랑이, 강아지
y_pred = [[0.6, 0.3, 0.1], [0.3, 0.6, 0.1], [0.1, 0.7, 0.2]]
cce = tf.keras.losses.CategoricalCrossentropy()
print(cce(y_true, y_pred).numpy())
# 1.936381

SparseCategoricalCrossentropy (CCE)

➡️ 정답 레이블이 onehot 인코딩이 아니고 정수로 주어질 때 사용(ex. 이미지를 "0(강아지)" vs "1(고양이)" vs "2(호랑이)" 으로 분류할 때)

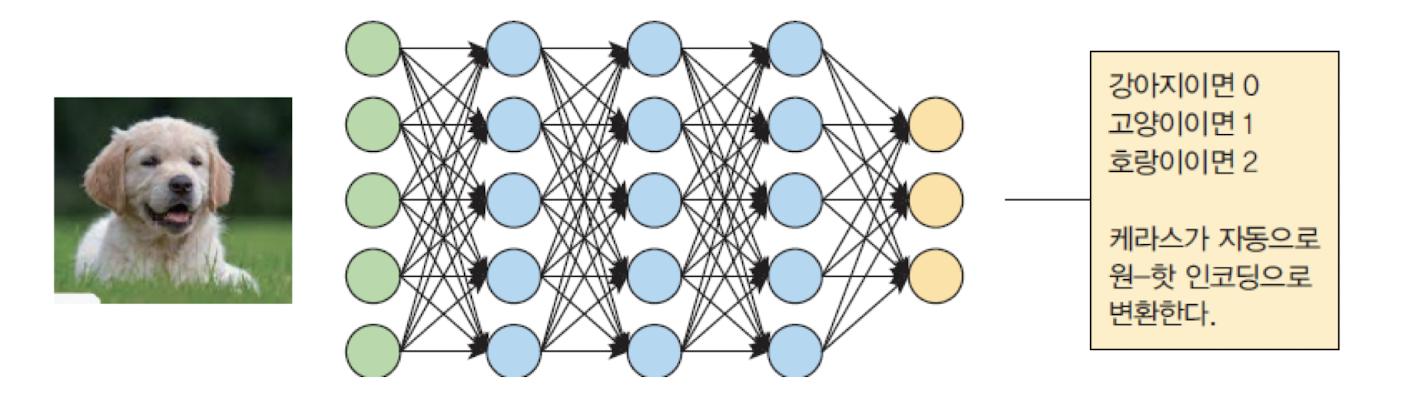
y_true = np.array([1, 2, 0])# 고양이, 호랑이, 강아지
y_pred = np.array([[0.6, 0.3, 0.1], [0.3, 0.6, 0.1], [0.1, 0.7, 0.2]])
scce = tf.keras.losses.SparseCategoricalCrossentropy()
print(scce(y_true, y_pred))
# 1.936381

MeanSquaredError

➡️ 회귀문제에서 예측값과 실제값 사이의 평균제곱오차를 계산할 때 사용한다.

y_true = [ 12 , 20 , 29 , 60 ]
y_pred = [ 14 , 18 , 27 , 55 ]
mse = tf.keras.losses.MeanSquaredError ()
print(mse(y_true, y_pred).numpy())
# 9.25

사용자 지정 손실함수 만들기

➡️ 실제값과 예측값을 매개변수로 사용하는 함수를 정의하여 만들 수 있다.
➡️ 모델의 컴파일 단계에서 함수를 전달하여 작성한다.

def custom_loss_function(y_true, y_pred) :
	squared_difference = tf.square (y_true-y_pred)
	return tf.reduce_mean (squared_difference, axis = -1 )

model.compile(optimizer=‘adam’, loss= custom_loss_function)

---

✅ 가중치 초기화 문제 (Weight initialization problem)

• 가중치를 0으로 초기화하면 역전파가 제대로 이뤄지지 않는다.

• 모든 가중치가 동일하면 노드들이 동일한 역할만 하게 되므로 대칭을 깨야 한다.

  가중치가 동일할 때의 문제점

  

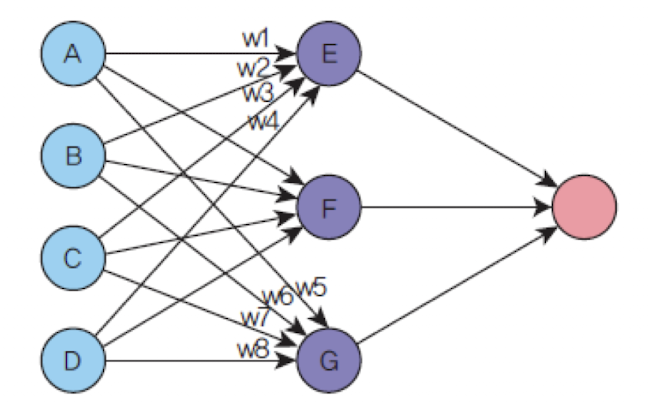
• 이를 위해 가중치는 난수로 초기화해야 한다.

• 너무 큰 초기 가중치는 그래디언트 폭발을 유발하여 학습이 발산하게 된다.

위 식에서 가중치가 0이라면 델타가 전달되지 않는다.

가중치 초기화 방법

➡️ Xavier 방법

• 분산 $var(w_i)=\frac{1}{N_{in}}$ 을 가지는 정규분표에서 난수를 추출하는 것을 제안하였다.
• 여기서 $N_{in}$은 유닛으로 들어오는 간선의 개수이고 $N_{out}$은 유닛에서 나가는 간선의 개수이다.

➡️ He의 방법

• 분산 $var(w_i)=\frac{2}{N_{in}+N_{out}}$ 을 가지는 정규분포에서 난수를 추출하는 것을 제안하였다.

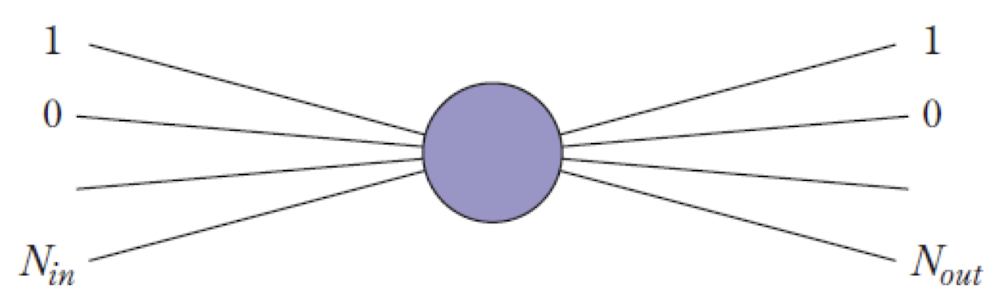
W = np.random.randn(N_in, N_out)*np.sqrt(1/N_in) # Xavier의 방법
W = np.random.randn(N_in, N_out)*np.sqrt(2/(N_in+N_out)) # He의 방법

케라스에서의 가중치 초기화 방법

# layers, initializers 모듈 import
from tensorflow.keras import layers
from tensorflow.keras import initializers

# initializers를 이용하여 가중치 초기화
layer = layers.Dense(units=64, kernel_initializer=initializers.RandomNormal(stddev=0.01),
bias_initializer=initializers.Zeros())

# 문자열 식별자를 통해 전달
layer = layers.Dense(units=64, kernel_initializer='random_normal', bias_initializer='zeros')

# RandomNormal 클래스: 정규 분포로 텐서를 생성하는 이니셜라이저
initializer = tf.keras.initializers.RandomNormal(mean=0, stddev=1.)
layers = tf.keras.layers.Dense(3, kernel_initializer=initializer)

# RandomUniform 클래스: 균일 분포로 텐서를 생성하는 이니셜라이저
initializer = tf.keras.initializers.RandomUniform(minval=0, maxval=1.)
layers = tf.keras.layers.Dense(3, kernel_initializer=initializer)

---

✅ 범주형 데이터 처리 문제 (Categorical data problem)

입력 데이터 중에는 “male”, “female”과 같이 카테고리를 가지는 데이터들이 아주 많다.
➡️ 숫자로 바꾸어 주어야 함

for ix in train.index:
	if train.loc[ix, 'Sex']=="male":
		train.loc[ix, 'Sex']=1
	else:
		train.loc[ix, 'Sex']=0

🔍 범주형 변수를 인코딩하는 3가지 방법

• 정수 인코딩(Integer Encoding): 각 레이블이 정수로 매핑되는 경우
• 원-핫 인코딩(One-Hot Encoding): 각 레이블이 이진 벡터에 매핑되는 경우
• 임베딩(Embedding): 범주의 분산된 표현이 학습되는 경우 → 추후 포스팅에 다룸

정수 인코딩

• sklearn 라이브러리가 제공하는 Label Encoder 클래스를 사용

import numpy as np
X = np.array([['Korea', 44, 7200], ['Japan', 27, 4800], ['China', 30, 6100]])

from sklearn.preprocessing import LabelEncoder
labelencoder = LabelEncoder()
X[:, 0] = labelencoder.fit_transform(X[:, 0])
print(X)

[['2' '44' '7200']
['1' '27' '4800']
['0' '30' '6100']]

onehot 인코딩(sklearn 사용)

import numpy as np
X = np.array([['Korea', 38, 7200], ['Japan', 27, 4800], ['China', 30, 3100]])

from sklearn.preprocessing import OneHotEncoder
onehotencoder = OneHotEncoder()

# 원하는 열을 뽑아서 2차원 배열로 만들어서 전달하여야 한다.
XX = onehotencoder.fit_transform(X[:,0].reshape(-1,1)).toarray()
print(XX)

X = np.delete(X, [0], axis=1) # 0번째 열 삭제
X = np.concatenate((XX, X), axis = 1) # X와 XX를 붙인다.
print(X)

[[0. 0. 1.]
[0. 1. 0.]
[1. 0. 0.]]
[['0.0' '0.0' '1.0' '38' '7200']
['0.0' '1.0' '0.0' '27' '4800']
['1.0' '0.0' '0.0' '30' '3100']]

onehot 인코딩(Keras 사용)

• to_categorical()을 호출하여 구현

class_vector =[2, 6, 6, 1]

from tensorflow.keras.utils import to_categorical
output = to_categorical(class_vector, num_classes = 7)
print(output)

[[0 0 1 0 0 0 0]
[0 0 0 0 0 0 1]
[0 0 0 0 0 0 1]
[0 1 0 0 0 0 0]]

---

✅ 데이터 정규화 문제 (Data normalization problem)

• 신경망은 입력마다 다른 범위의 매개변수를 학습하므로, 입력 값의 범위가 중요하다.

• 부동소수점 정밀도 문제를 피하려면 입력을 대략 -1.0 ~ 1.0 범위로 맞추는 것이 좋다.

• 일반적으로 평균이 0이 되도록 정규화하고, 범위를 일정하게 조정한다.

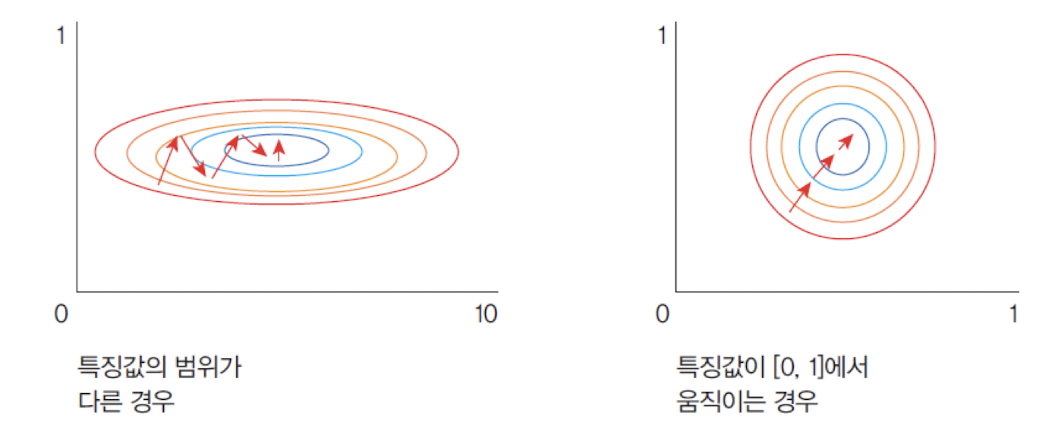
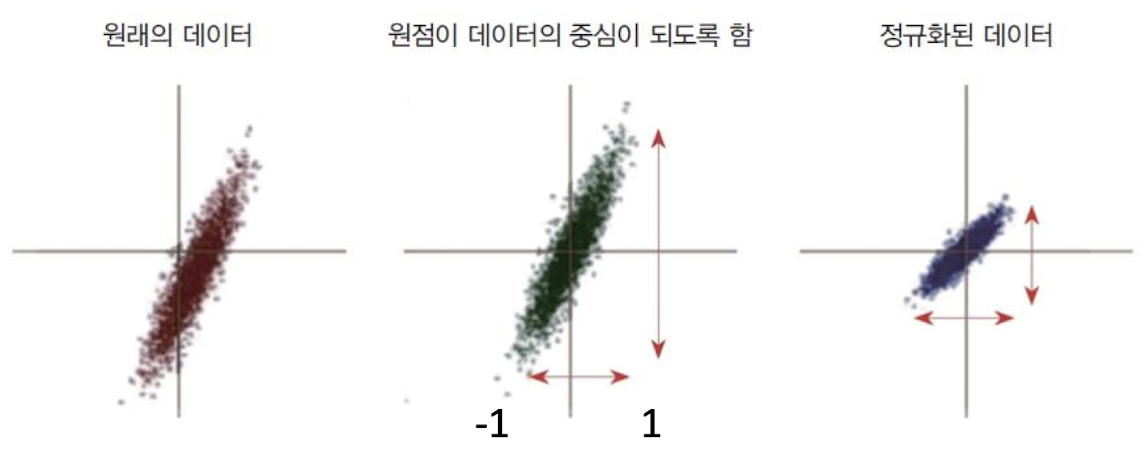
정규화 예제

➡️ 사람의 나이, 성별, 연간 수입을 기준으로, 선호하는 자동차의 타입(세단 아니면 SUV)을 예측할 신경망을 만들고 싶다고 가정

나이, 성별, 연간수입, 자동차

[0]		30		male		3800		SUV
[1]		36		female		4200		SEDAN
[2]		52		male		4000		SUV
[3]		42		female		4400		SEDAN
	정규화필요	범주형데이터				원-핫인코딩

[0]	-1.23		-1.0		-1.34	(1.0 0.0)
[1]	-0.49		1.0			0.45	(0.0 1.0)
[2]	1.48		-1.0		-0.45	(1.0 0.0)
[3]	0.25		1.0			1.34	(0.0 1.0)

데이터 정규화 방법 (sklearn 사용)

sklearn의 MinmaxScaler 클래스는 다음의 Numpy 수식을 사용하여 정규화한다.

from sklearn.preprocessing import MinMaxScaler
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]

scaler = MinMaxScaler()
scaler.fit(data) # 최대값과 최소값을 알아낸다.
print(scaler.transform(data)) # 데이터를 변환한다.

[[0. 0. ]
[0.25 0.25]
[0.5 0.5 ]
[1. 1. ]]

데이터 정규화 방법 (Keras 사용)

데이터 정규화가 필요하면 케라스의 Normalization 레이어를 중간에 넣으면 된다.

• 1단계: 0~1 범위로 표준화

• 2단계: 원하는 범위 [min, max]로 스케일링

tf.keras.preprocessing.Normalization(
	axis=-1, dtype=None, mean=None, variance=None, **kwargs
)
# axis: 유지해야 하는 축, mean: 정규화 중 사용할 평균값, variance=정규화 중 사용할 분산값
# 이 레이어는 입력을 평균이 0이고 표준편차가 1인 분포로 정규화시킴

import tensorflow as tf
import numpy as np

adapt_data = np.array([[1.], [2.], [3.], [4.], [5.]], dtype=np.float32)
input_data = np.array([[1.], [2.], [3.]], np.float32)
layer = tf.keras.layers.Normalization()
layer.adapt(adapt_data)
layer(input_data)

#<tf.Tensor: shape=(3, 1), dtype=float32, numpy=
#array([[-1.4142135 ],
# [-0.70710677],
# [ 0. ]], dtype=float32)>

---

✅ 과잉 적합 문제 (Overfitting problem)

• 과잉 적합(overfitting)은 지나치게 훈련 데이터에 특화돼 실제 적용 시 좋지 못한 결과가 나오는 것을
  말한다.
• 과잉 적합은 신경망의 매개변수가 많을 때 발생한다.
• 훈련 데이터 외에 검증데이터를 사용하여 손실(MSE)를 계산해 보면 U shape의 학습 커브가 나온다.

➡️ 일반화에 실패

➡️ Variance-bias trade off ➡️ `훈련 데이터`의 손실값은 계속 `감소`하지만 `검증데이터`의 손실값은 `증가`하고 있음

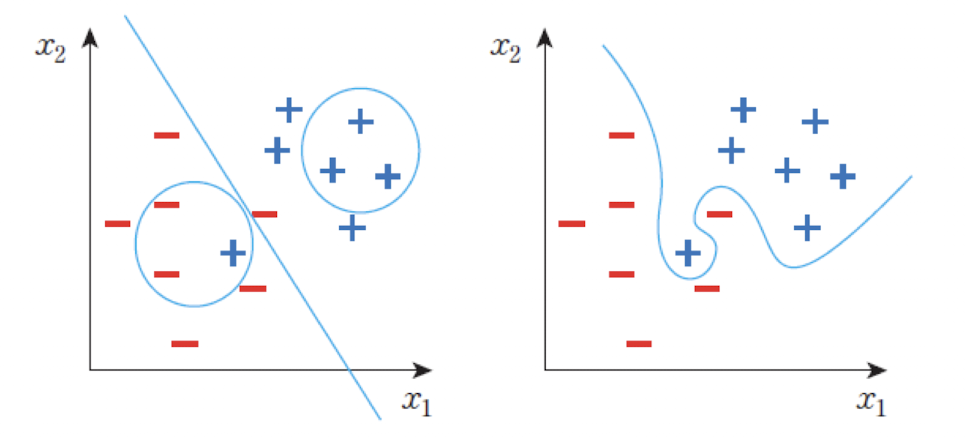
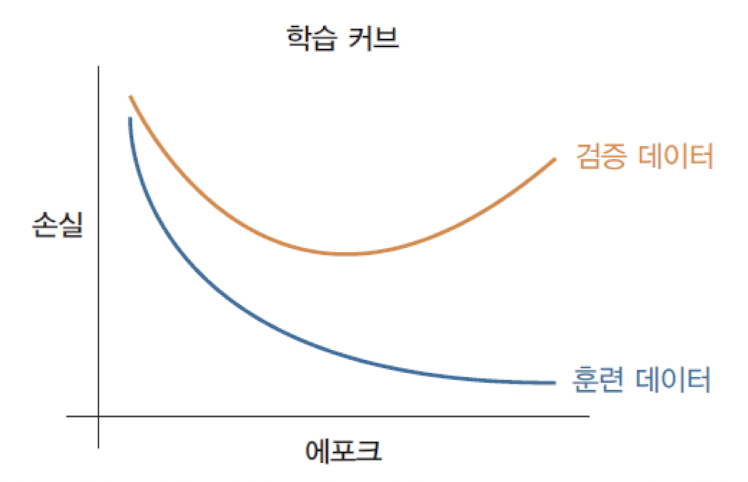
과잉 적합의 예

IMDB 영화 리뷰 데이터

import numpy as numpy
import tensorflow as tf
import matplotlib.pyplot as plt

# 데이터 다운로드 (상위 1000개 단어를 선택)
(train_data, train_labels), (test_data, test_labels) = \
	tf.keras.datasets.imdb.load_data(num_words=1000)

# 원-핫 인코딩으로 변환하는 함수
def one_hot_sequences(sequences, dimension=1000):
	results = numpy.zeros((len(sequences), dimension))
	for i, word_index in enumerate(sequences):
		results[i, word_index] = 1.
	return results

train_data = one_hot_sequences(train_data)
test_data = one_hot_sequences(test_data)

# 신경망 모델 구축
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(16, activation='relu', input_shape=(1000,)))
model.add(tf.keras.layers.Dense(16, activation='relu'))
model.add(tf.keras.layers.Dense(1, activation='sigmoid'))

model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])

# 신경망 훈련, 검증 데이터 전달
history = model.fit(train_data,
					train_labels,
					epochs=20,
					batch_size=512,
					validation_data=(test_data, test_labels),
					verbose=2)

# 훈련 데이터의 손실값과 검증 데이터의 손실값을 그래프에 출력
history_dict = history.history
loss_values = history_dict['loss'] # 훈련 데이터 손실값
val_loss_values = history_dict['val_loss'] # 검증 데이터 손실값
acc = history_dict['accuracy'] # 정확도
epochs = range(1, len(acc) + 1) # 에포크 수

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Loss Plot')
plt.ylabel('loss')
plt.xlabel('epochs')
plt.legend(['train error', 'val error'], loc='upper left')
plt.show()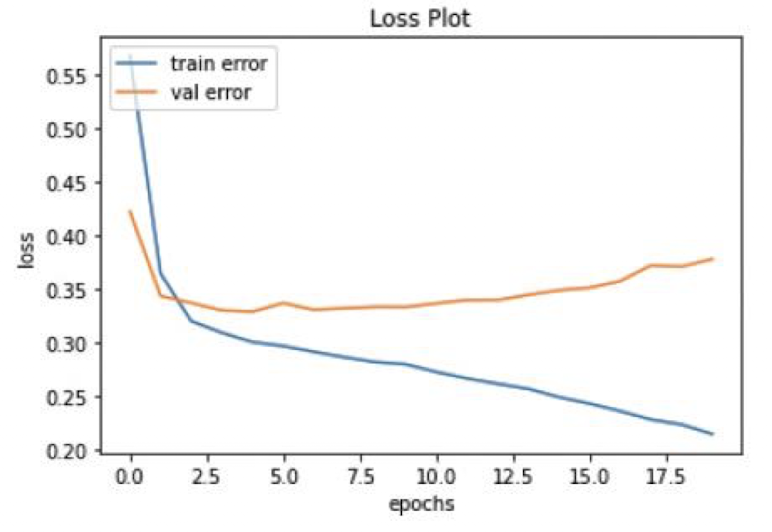

과잉 적합 방지 전략

가중치(weight)의 개수를 줄이거나 제한하고 훈련 데이터(traing data)의 양을 늘리면 된다.

• 조기 종료(early stopping): 검증 손실이 증가하면 훈련을 조기에 종료한다.
• 가중치 규제 방법(weight regularization): 가중치의 절대값을 제한한다.
• 드롭아웃 방법(dropout): 몇 개의 뉴런을 쉬게 한다.
• 데이터 증강 방법(data augmentation): 데이터를 많이 만든다.

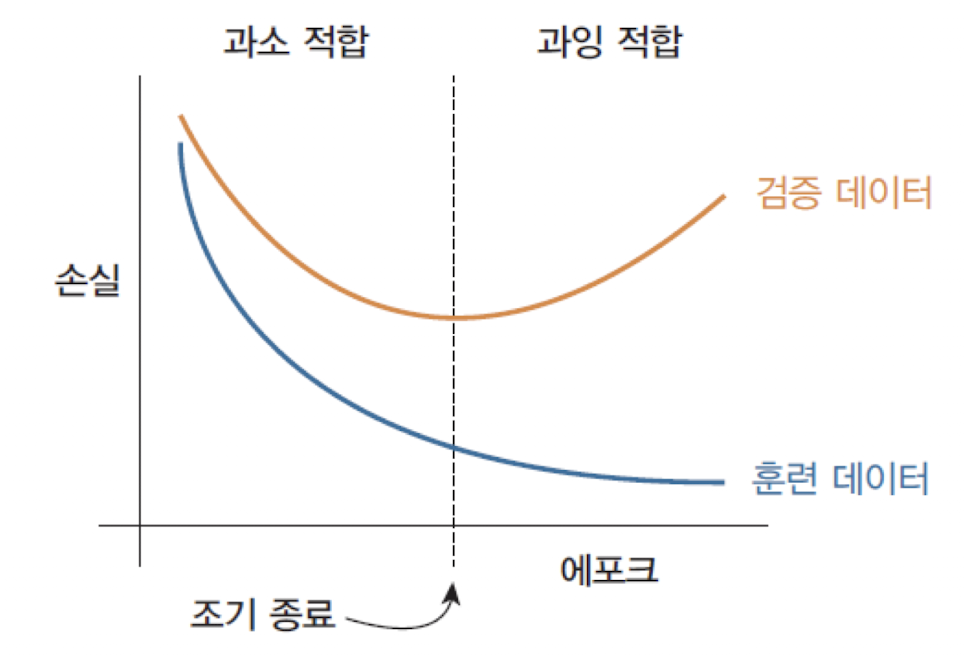
조기종료 (early stopping)

➡️ 모델이 노이즈를 너무 열심히 학습하면 학습 중에 검증 손실이 발생할 수 있다.
➡️ 검증 손실이 더 이상 감소하지 않는 것처럼 보일 때마다 훈련을 중단할 수 있다.

가중치 규제 (weight regularization)

➡️ 가중치의 값이 너무 크면, 판단 경계선이 복잡해지고 과잉 적합이 일어난다는 사실을 발견하였다.

• L1 규제: $\text{Loss} = \text{Cost} + \lambda \sum |W|$
• L2 규제: $\text{Loss} = \text{Cost} + \lambda \sum W^2$

➡️ L1 규제는 가중치를 0으로 만드는 단점이 있어서 L2규제를 더 많이 사용한다.

# 신경망 모델 구축
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(16, kernel_regularizer=tf.keras.regularizers.l2(0.001), activation='relu', input_shape=(1000,)))
model.add(tf.keras.layers.Dense(16, kernel_regularizer=tf.keras.regularizers.l2(0.001), activation='relu'))
model.add(tf.keras.layers.Dense(1, activation='sigmoid'))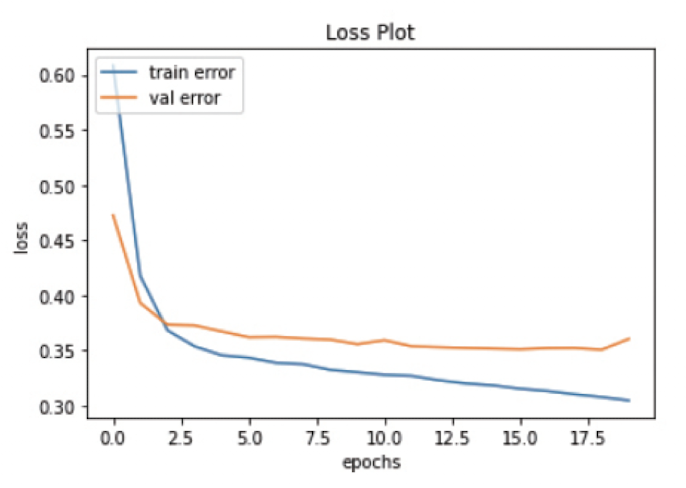

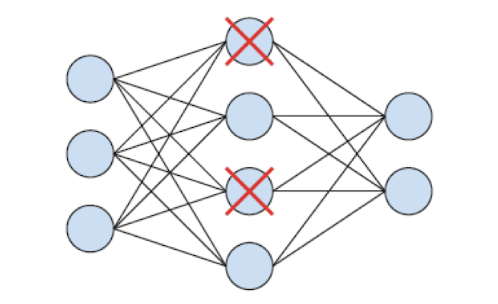
드롭아웃 (dropout)

➡️ 드롭아웃은 몇 개의 노드들을 학습 과정에서 랜덤하게 제외하는 것이다.
➡️ 보통 0.2에서 0.5사이의 값을 사용한다.

# 신경망 모델 구축
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(tf.keras.layers.Dropout(0.5))
model.add(tf.keras.layers.Dense(16, activation='relu'))
model.add(tf.keras.layers.Dropout(0.5))
model.add(tf.keras.layers.Dense(1, activation='sigmoid'))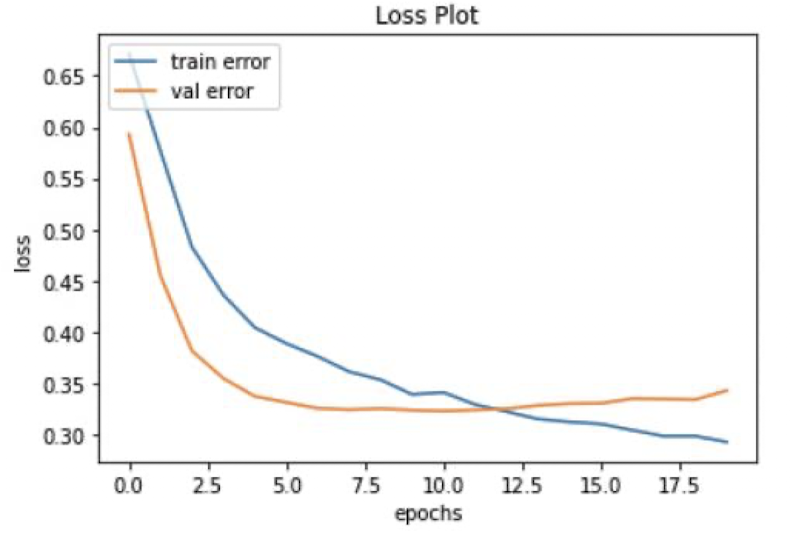

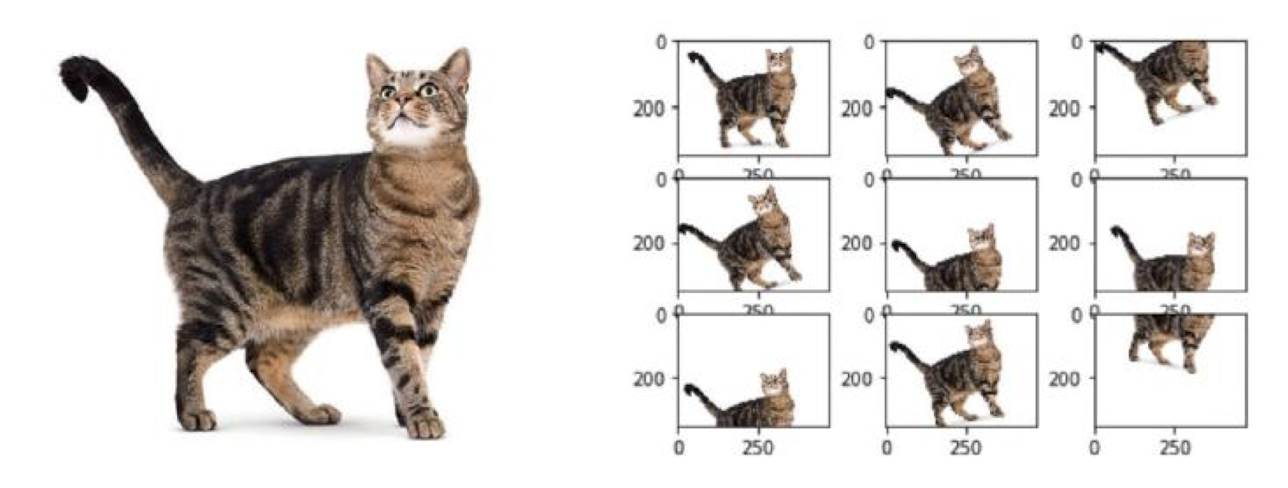
데이터 증강 방법 (data augmentation)

➡️ 소량의 훈련 데이터에서 많은 훈련 데이터를 뽑아내는 방법이다.
➡️ 이미지를 좌우로 확대한다거나 회전시켜서 변형된 이미지를 생성하여 이것을 새로운 훈련 데이터로 사용하는 방법이다.

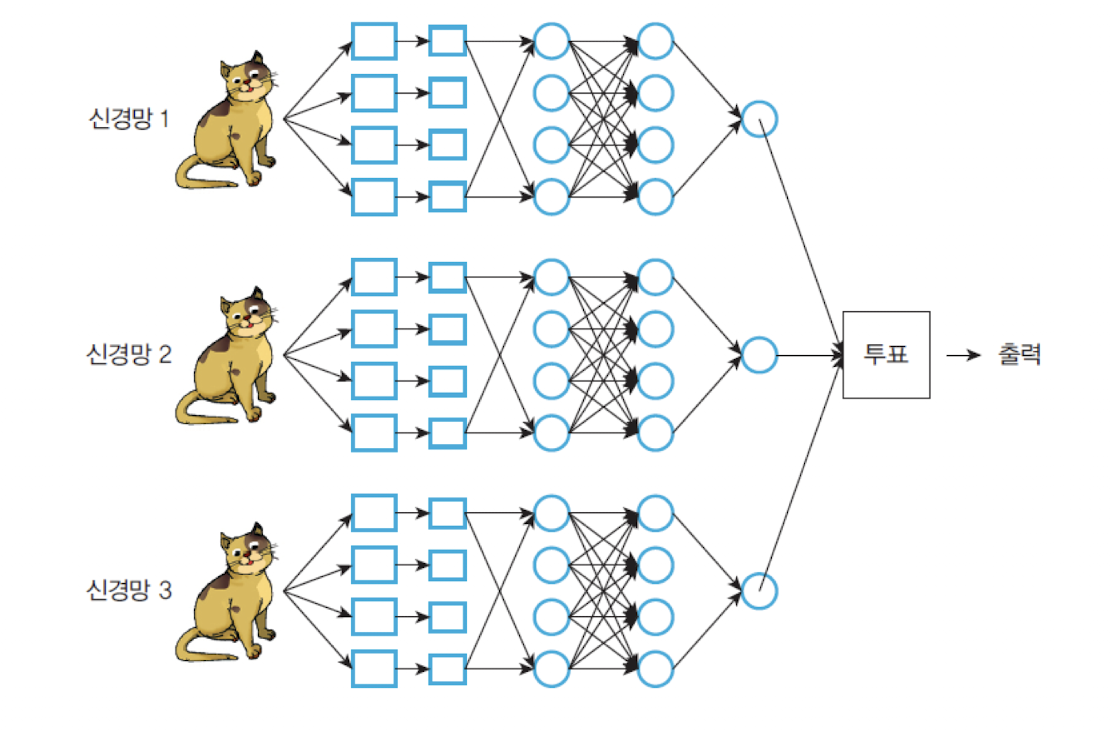
앙상블 (ensemble)

➡️ 여러 전문가를 동시에 훈련시키는 것과 같다. 이 방법은 동일한 딥러닝 신경망을 N개를 만드는 것이다.

• 약 2~5%정도의 성능 향상을 기대할 수 있다.

➡️ 각 신경망을 독립적으로 학습시킨 후에 마지막에 합치는 것이다.