⁉️ 딥러닝, 언제 쓰는 게 좋을까?

딥러닝은 정말 강력한 도구지만, 언제나 정답은 아니다.

CNN과 RNN의 성공 사례

• CNN은 이미지 분류 분야에서 큰 성공을 거뒀고, 현재는 의료 진단 분야로도 확장 중
• RNN은 음성 모델링, 기계 번역, 시계열 예측 분야에서 주로 사용됨

하지만 항상 쓸 필요는 없다

• 딥러닝이 잘 작동하는 환경: 신호-대-잡음비(signal-to-noise ratio) 가 높은 경우
• 잡음이 많은 데이터(비정형일 경우)에서는 단순한 모델이 더 나을 수 있다

예시
NYSE 데이터: AR(5) 모델이 RNN만큼 잘 작동함 (훨씬 단순함)
IMDB 리뷰: glmnet으로 학습한 선형 모델이 RNN보다 성능이 좋았고, 해석도 쉬움

---

Fitting Neural Networks

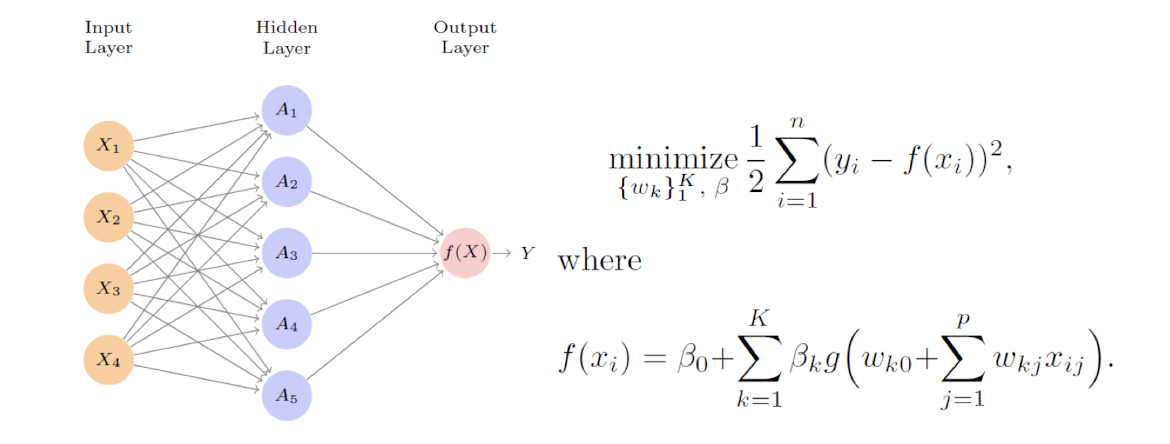
신경망 학습은 비선형, 비볼록(non-convex) 문제라 최적화가 어렵다.

Local minimum을 피해서 Global minimum을 찾는 것이 중요하다. $\theta$가 1차원이 아니어 찾기 힘든 난제다

신경망 학습은 이런 복잡한 손실 지형 위에서 최적화가 이뤄진다.
완벽한 해는 어려울 수 있지만, 좋은 시작점 + 좋은 알고리즘(SGD, Adam) 으로도 꽤 괜찮은 성능에 도달할 수 있다!

---

📉 Gradient Descent: 경사하강법

신경망 학습은 보통 경사하강법(Gradient Descent) 을 통해 손실 함수를 최소화한다.

✔️ 기본 알고리즘

1. 초기값 $\theta_0$을 임의로 설정하고, $t=0$
2. 반복 수행:
   • 기울기 방향으로 조금 이동하여 $\theta$ 값을 업데이트
   • $R(\theta_{t+1}) < R(\theta_{t})$ 가 되도록 업데이트

✔️ 수식

• 기울기(gradient) 벡터 계산:

  $\nabla R(\theta_t) = \left. \frac{\partial R(\theta)}{\partial \theta} \right|_{\theta = \theta_t}$

• 업데이트 규칙:

  $\theta_{t+1} = \theta_t - \rho \nabla R(\theta_t)$
  • $\rho$: 학습률(learning rate) – 작을수록 천천히, 클수록 빠르게 움직임 (예: 0.001)

🖇️ 로컬 vs 글로벌 최소값

• 시작 위치에 따라 로컬 최소값에 머물 수 있음
• 앞서 본 그래프처럼, $\theta_0$의 위치가 조금만 달랐다면 다른 최소점에 도달했을 것
• 고차원에서는 이 현상이 더 복잡해짐 (직관적으로 파악하기 어려움)

Gradient Descent는 "내리막길을 따라 내려간다"는 아주 직관적인 원리로 작동한다.
손실 함수의 기울기를 계산하고, 그 반대 방향으로 조금씩 이동하며 최적의 파라미터를 찾아간다.

---

📈 Backpropagation

✔️ 손실 함수 구성

전체 손실:

• 각 데이터 $i$에 대한 손실:
  $R_i(\theta) = \frac{1}{2} \left( y_i - f_\theta(x_i) \right)^2$
  여기서 $f_\theta(x_i)$는 은닉층이 하나인 FNN의 출력:
  $f_\theta(x_i) = \beta_0 + \sum_{k=1}^{K} \beta_k \cdot g(z_{ik})$
  그리고 $z_{ik} = w_{k0} + \sum_{j=1}^{p} w_{kj} x_{ij}$

🖇️ 역전파: 체인룰로 미분하기

출력층 계수에 대한 미분:

은닉층 가중치에 대한 미분:

• Backpropagation은 체인 룰을 활용해서 출력층 → 은닉층 → 입력층으로 기울기를 전파함
• 계산량을 줄이고 효율적으로 학습할 수 있도록 설계된 핵심 알고리즘
• 딥러닝이 가능해진 기술적 기반 중 하나

✍️ 수식은 복잡해 보여도, 결국 "오차를 각 층으로 나눠서 책임지게 만든다"는 게 핵심!!

---

🛒 Stochastic Gradient Descent (SGD)

✔️ 기존 gradient descent의 문제점

• 모든 데이터를 이용한 gradient 계산은 느리고 계산량이 많다
• 특히 학습률(learning rate) 이 작을 경우, 수렴 속도가 더 느려짐

💡 SGD의 아이디어

전체 데이터를 쓰지 않고, 랜덤한 작은 묶음(minibatch) 만으로도 gradient를 근사한다!!

• 예: MNIST 데이터 (전체 60,000개 → 학습용 48K, 검증용 12K)
• 미니배치 크기: 128개
• 1 epoch = 전체 데이터를 1회 학습 → $\frac{48{,}000}{128} = 375$개의 미니배치 업데이트

✔️ Early Stopping

• 검증 손실(validation loss)이 30 epoch 이후 오히려 증가
• → 조기 종료(Early Stopping) 를 통해 과적합을 막는 정규화 기법으로 활용 가능

✅ SGD는 빠르고, 일반화 성능도 좋다.
여기에 Early Stopping 같은 전략까지 더하면, 더 안정적인 학습이 가능해진다.

---

📊 Regularization

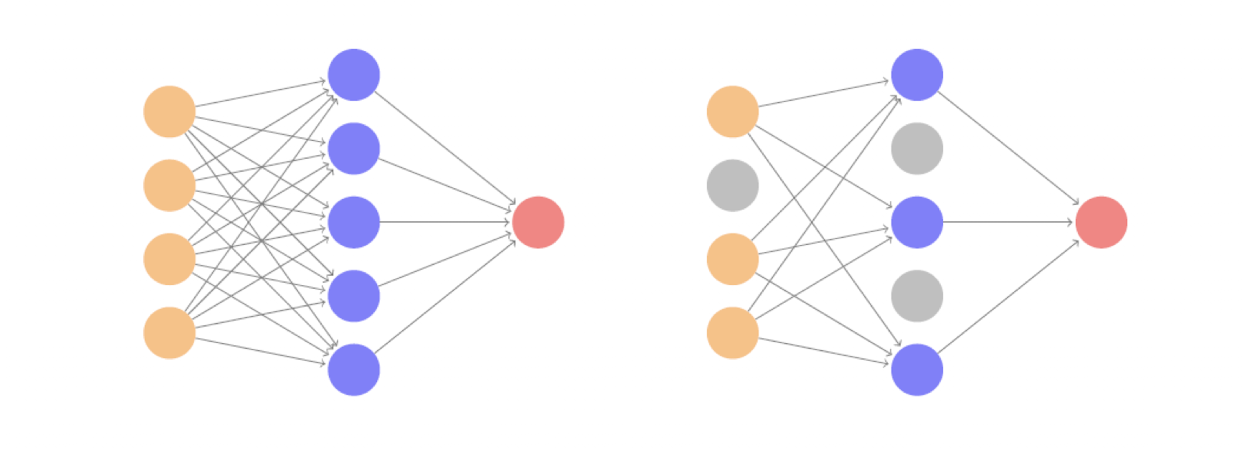
• Dropout은 학습 중 매번 일부 뉴런을 확률 $\phi$ 로 랜덤하게 제거(drop)하는 방식이다.

• 제거된 뉴런을 제외하고 학습하며, 남은 뉴런의 출력은 $\frac{1}{1 - \phi}$만큼 스케일업하여 보정한다.

• 이런 방식은 과적합을 막고, 매번 다른 서브 네트워크를 학습하는 효과를 만들어 앙상블 학습과 유사하다.

• 선형 회귀처럼 단순한 모델에서는 릿지 정규화(ridge) 와 유사한 효과를 가지며,
  랜덤 포레스트처럼 일부 입력을 랜덤하게 제거하는 방식과도 비슷하다.

---

✅ Data augmentation

데이터를 늘리는 동시에, 모델의 일반화 능력까지 향상시키는 똑똑한 전략

• 데이터 증강(data augmentation) 은 훈련 데이터를 변형해 더 많은 학습 샘플을 만드는 기법이다.
• 특히 CNN + SGD 조합에서 효과가 크며, 이미지 분류에서 자주 쓰인다.

어떻게 작동하나?

• 각 이미지에 대해 자연스러운 변형(transform) 을 적용:
  • 예: 회전, 확대/축소, 이동, 밝기 변화 등
• 변형된 이미지도 원래와 같은 라벨을 유지 (예: 여전히 "tiger")

효과

• 하나의 이미지 주변에 여러 변형된 이미지들을 만들어 “이미지 구름” 을 형성
• Dropout처럼 과적합을 막고, ridge 정규화와 유사한 효과를 줌
• 모델이 특정 입력에 과도하게 의존하지 않고, 더 일반적인 패턴을 학습하게 됨

---

✅ Double Descent

기존 이론: Bias-Variance Trade-off

• 모델 복잡도가 커지면 편향(bias) 은 줄고, 분산(variance) 은 커짐
• 그래서 일반화 오류는 U자 형태로 나타남 → 너무 단순해도, 너무 복잡해도 안 좋다

그런데… 신경망은 다르다?

• 은닉 유닛을 많이 쓰거나, 층 수를 늘려서 복잡도를 높이면:
  • 훈련 오차는 0까지 감소
  • 그런데도 테스트 성능이 오히려 더 좋아지는 경우가 많다!
• 심지어 모델을 더 크게 만들어도, 다시 일반화 성능이 향상되는 현상이 나타남

에러 곡선이 한 번 꺾였다가 다시 내려가는 "W자 모양" 을 보이는 것
첫 번째 디센트: 전통적인 bias-variance 곡선
두 번째 디센트: 과적합을 뚫고, 더 큰 모델이 오히려 더 잘 일반화하는 영역

신경망은 복잡한 구조에서도 과적합되지 않고, 오히려 훈련 오차 0이 일반화 성능이 좋을 때도 있다

🖇️ Simulation Double Descent

• 데이터 생성:

  $y = \sin(x) + \epsilon, \quad x \sim \mathcal{U}[-5,\ 5], \quad \epsilon \sim \mathcal{N}(0,\ 0.3^2)$

• 훈련 데이터: 20개 / 테스트 데이터: 10,000개

• 모델: 자연 스플라인(natural spline)을 사용한 선형 회귀

  $\hat{y}_i = \sum_{j=1}^{d} \hat{\beta}_j N_j(x_i)$

• $d=20$: 훈련 데이터를 정확히 맞춤 (잔차 = 0), 해는 유일

• $d>20$: 여전히 잔차는 0이지만, 해는 여러 개 → 그중 $\sum_{j=1}^{d} \hat{\beta}_j^2$ 가 가장 작은 해(minimum norm solution)를 선택

Double Descent Error Curve

• $d≤20$: OLS 회귀 영역 → 전통적인 bias-variance trade-off 발생
• $d=20$: 훈련 데이터를 완벽히 맞춤 (잔차 0), 해는 유일
• $d>20$: 여전히 잔차 0 가능하지만, 해가 여러 개 → minimum norm solution 선택.
  이때, $\sum_{j=1}^{d} \hat{\beta}_j^2$ 값이 감소하면서 덜 요동치는(wiggly) 해가 선택됨

복잡도가 늘어도 해의 norm이 작아지면서, 오히려 일반화 성능이 다시 좋아지는 double descent 현상이 나타난다!

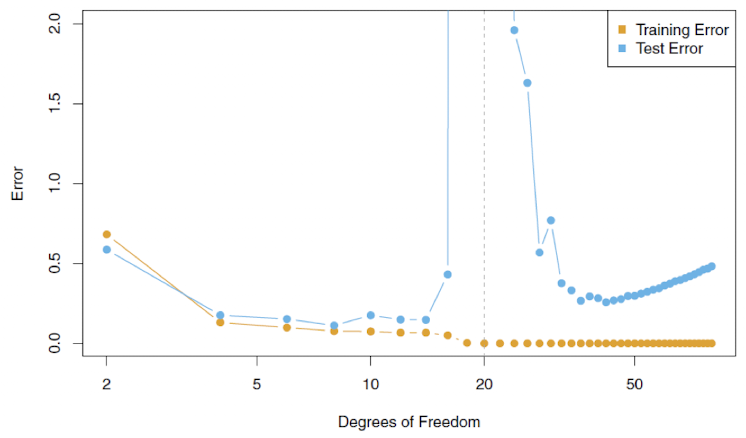
$d=20$에서는 훈련 데이터를 정확히 맞추는 zero-residual 해를 얻기 빡빡함
$d>20$에서는 해가 많아지므로, 더 매끄럽고 덜 요동치는(wiggly) 해 중 $\sum_{j=1}^{d} \hat{\beta}_j^2$이 가장 작은 해(minimum norm) 를 선택할 수 있음

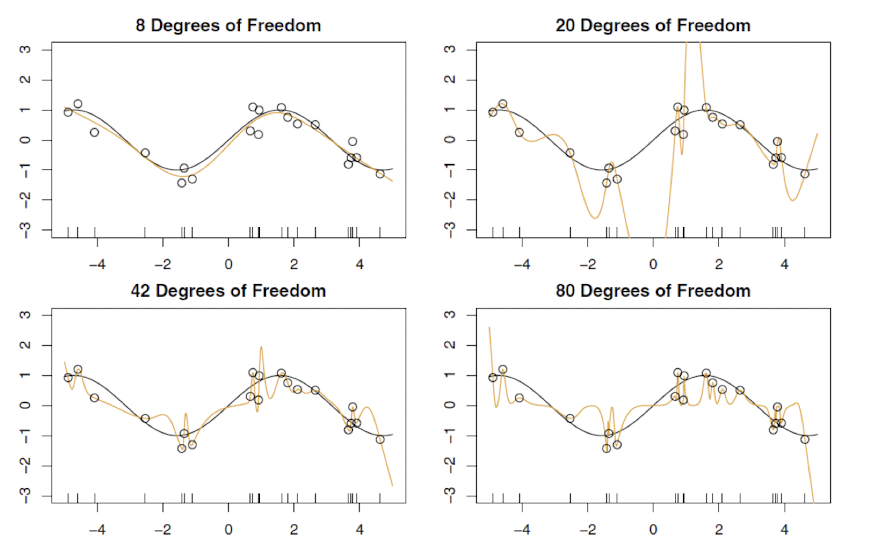
자유도가 더 높을수록, 동일하게 잔차 0을 유지하면서도 더 부드러운 함수를 선택할 수 있게 된다!

---

✍️ Summary

넓은 선형 모델에서 파라미터 수가 적고 데이터가 많을 때, 작은 스텝 크기의 SGD는 잔차 0이면서 최소 norm을 갖는 해로 수렴한다.

이때의 SGD 경로(stochastic gradient flow) 는 릿지 회귀 해의 경로와 유사한 성질을 가진다.

이와 유사하게, 딥하고 넓은 신경망도 SGD로 잔차 0까지 학습했을 때 일반화 성능이 뛰어난 해를 찾을 수 있다.

특히 이미지 분류처럼 신호-대-잡음비가 높은 문제에서는 과적합 위험이 낮고, 잔차 0인 해가 실제로 의미 있는 신호를 잘 포착하는 경우가 많다.

---